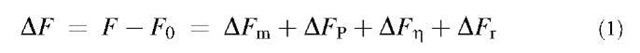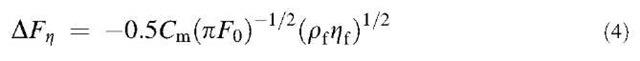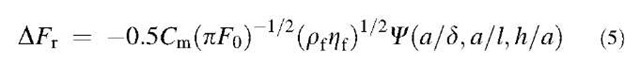Microweighing in Supercritical Carbon Dioxide Part 1 (Nanotechnology)

INTRODUCTION

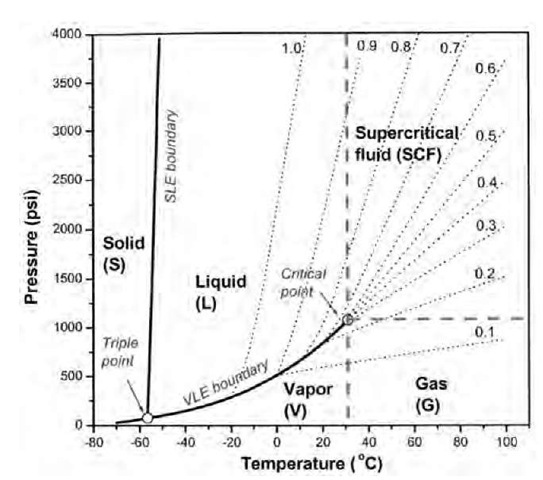
Carbon dioxide (CO2), when heated and pressurized above its critical temperature (31 °C) and pressure (7.377 MPa), is identified as being in a fourth, supercritical state with properties intermediate between liquid and gas (Table 1). At the critical point, the interface of CO2 liquid and vapor starts to vanish (Fig. 1). Supercritical CO2 (scCO2) has liquid-like densities providing good solvent capability, gas-like viscosities, and diffusivities to benefit mass transport, and a nonhazardous nature for the environment. Because of these properties and other advantages of CO2 over organic solvents such as low surface tension and low cost, scCO2 has received increasing industrial and research attention in a variety of processes such as extraction,[3,4] cleaning,[5,6] polymer synthesis,[7,8] and more recently microelectronics processing.1-9,10-1 CO2 has been proposed to serve as an energy-efficient and environmentally benign solvent platform.1-11-1 The real-time monitoring of the time-dependent mass change is crucial to understanding, characterizing, designing, and controlling the aforementioned processes. However, this monitoring presents a number of challenges because of the difficulty in applying various detection methods under high-pressure conditions.

In this topic, two microweighing techniques in sc CO2, gravimetric and piezoelectric, are reviewed. A comparison is made between two representatives of these techniques: the magnetic suspension balance (gravimetric) and the quartz crystal microbalance (QCM, piezoelectric). The QCM theory in high-pressure fluids is briefly introduced, followed by a summary of recent research which includes 1) the experimental verification of QCM theory; 2) the scCO2 adsorption on metal surfaces; and 3) the dissolution of polymer films for applications in scCO2-based lithography processes. Finally, the application of QCM in absorption, solubility, and other surface-specific processes in scCO2 will be reviewed to highlight the versatility of the QCM technique.

MICROWEIGHING TECHNIQUES: GRAVIMETRIC AND PIEZOELECTRIC

Many important physical and chemical processes can be monitored by observing the associated mass changes. Currently, two microweighing techniques, gravimetric and piezoelectric, have been widely used as an analytical tool for research and applied applications. Gravimetric microbalances are the most direct technique to measure mass variations at the microgram level. However, in a number of cases, most conventional gravimetric micro-balances such as spring, beam, and torsional balances are not designed for the operation under extreme conditions. The extreme conditions are usually defined as conditions of high pressures (> 1450 psi), viscous fluids, and/or high temperatures. In order to adapt the conventional gravimetric balances to work under extreme pressures, some researchers1-12,13-1 have designed a high-pressure container to include both the microbalance and the sample. This not only greatly increases the system expenses, structural complexity, and operational difficulties, but also sacrifices the capability under high temperatures (> 125°C) because of the microbalance working conditions. Jwayyed et al.[13] modified a commercial high-pressure microbalance (Cahn C-1000 balance) by redesigning the container (nipple shape with 30 cm o.d. and 25 cm height) for use in scCO2. They were only able to extend the pressure limit from 1600 to 3000 psi.

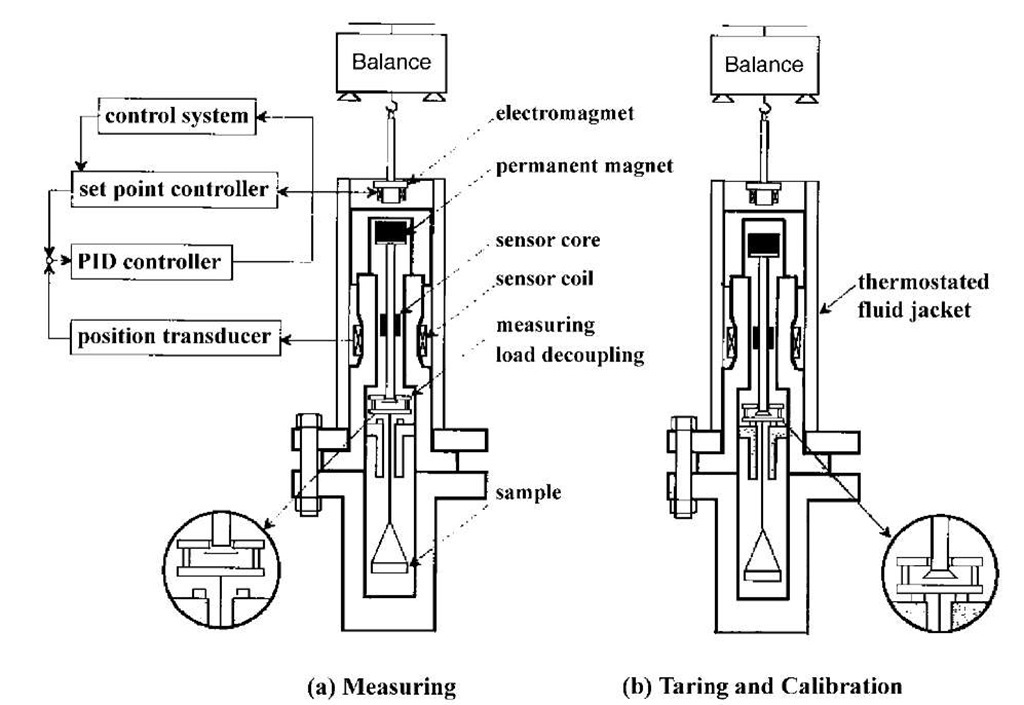
In recent years, some researchers[14,15- have been able to design a unique balance, a magnetic suspension balance (MSB), for mass measurements under extreme conditions (>3000 psi). The MSB takes advantage of the principle of magnetic coupling to isolate the balance from the sample that is contained in a small pressure cell (Fig. 2), while maintaining most features of the traditional microbal-ances. Using this magnetic suspension coupling, the measured force is transmitted from the pressure cell to the microbalance that is located in the ambient environment. Such novel design eliminates the large container, enables the capability of mass determinations under extreme conditions, and makes realistic applications of gravimetric techniques in CO2-based processes. The MSB has primarily been applied to determine the adsorption/ absorption and diffusivity of scCO2 in addition to other solutes on/in bulk solid materials under static condi-tions.[16-22] Applications of MSB for other chemical processes and applications under dynamic (flowing) conditions are rarely found in the literature.

Table 1 Physical properties of gas, liquid, and supercritical fluid (order of magnitude)

	Density	Diffusivity	Viscosity
	(g/cm3)	(cm2/sec)	(g/cm/sec)
Gas	1 x 10" 3	1 x 10"1	1 x 10" 4
Liquid	1.0	5 x 10" 6	1 x 10" 2
Supercritical fluid	3 x 10"1	1 x 10" 3	1 x 10" 4

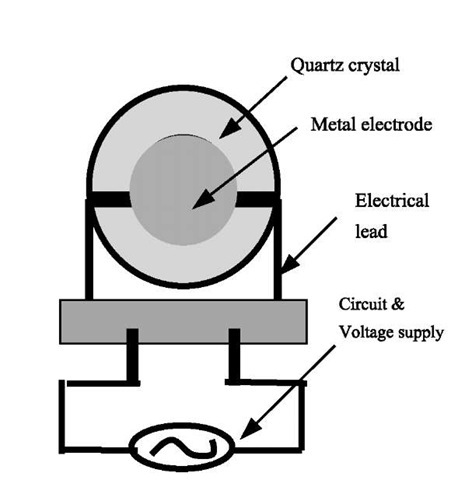
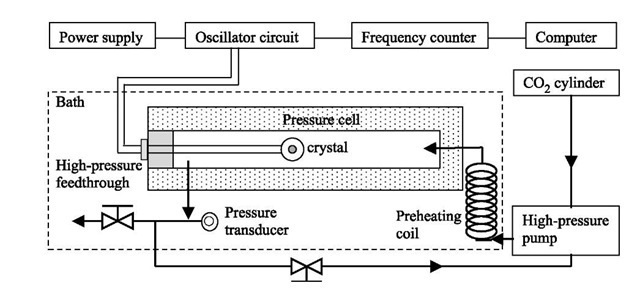
Piezoelectric quartz crystal resonators take advantage of the electric polarization that occurs when the crystal is subjected to a mechanical stress.[23] Several different devices operate using the piezoelectric technique according to the modes of electromechanical coupling, such as modes of thickness shear, face shear, and surface acoustic wave.[24] The AT-cut thickness-shear mode resonator, commonly referred to QCM, is the most widely used piezoelectric mass sensor.[25] The QCM consists of a thin quartz disk with two metal electrodes plated on its two opposite surfaces (Fig. 3). The QCM is a powerful microweighing tool for detecting in situ the mass changes to the ng/cm2 level of sensitivity. In the last decade, there has been increased application of the QCM for studies of a wide range of chemical processes and chemistries on surfaces and in thin films.[23-29] There are few difficulties for QCM applications under extreme conditions, because of the rigidity and chemical inertness of the quartz crystals and the elimination of any connection except the supply of electricity. Rigid electrical leads are commonly used to hold the crystal in place and excite the sensor that is contained in the pressure cell (Fig. 4). The QCM has been applied to many scCO2-based processes and chemistries in bulk phases or at surface films; they will be summarized later in the following sections.

Table 2 summarizes a comparison of the performance of MSB with QCM for the microweighing in scCO2. As can be seen, the QCM is a more powerful and versatile microweighing tool in scCO2 than the MSB, mainly owing to its low cost, conceptual simplicity, high mass sensitivity, wide range of applications, rapid time response, and miniature and simple construction. In particular, the nanogram-level sensitivity enables the QCM as a possible technique that can be utilized to study interfacial processes related to nanotechnologies and nanomaterials.

QUARTZ CRYSTAL MICROBALANCE THEORY IN HIGH-PRESSURE FLUIDS

Fundamentals

As the QCM is piezoelectric, an external electrical potential applied across the electrodes produces internal mechanical stress. This stress induces an acoustic wave that propagates through the crystal and meets minimum impedance when the thickness of the crystal is a multiple of a half wavelength of the acoustic wave. A resonant oscillation is achieved by including the crystal into an oscillation circuit in which the electric and the mechanical oscillation are close to the fundamental frequency (F0) of the crystal.[25,26]

When a crystal is immersed in a fluid, any frequency shift from its fundamental value (F0) in vacuum can be observed because of contributions from 1) mass sorption or desorption from the crystal surface; 2) pressure; 3) density and viscosity of the fluid surrounding the crystal; and 4) surface roughness of the crystal. The following expression has been established to describe changes in the crystal frequency, AF, due to the aforementioned effects:[30]

where F is the measured frequency of quartz, AFm relates to mass loading, AFP is dependent on pressure, AFZ changes with density and viscosity, and AFr is a function of surface roughness.

Fig. 1 Phase diagram for CO2 with constant density lines (dot lines, g/cm3). Above the critical point (31°C and 1070 psi), the vapor-liquid equilibrium (VLE) boundary vanishes, and the supercritical state is observed. The dash lines do not represent a boundary, but for the convenience to distinguish different states of CO2.

Fig. 2 A typical magnetic suspension balance (MSB).

According to the well-known Sauerbrey equation,[31] AFm is directly proportional to the mass loading on the crystal:

where mq is the shear modulus of quartz, pq is the density of the crystal, Am is the film mass per real surface area, n is the number of faces of the crystal exposed, and Cm is the mass sensitivity of QCM, which is a function of the characteristic properties (F0, mq, and pq) of the quartz crystal. Eq. 2 applies only if the adsorbed mass is much less than the mass of the crystal and it assumes this mass is firmly attached to the surface; hence the material moves together with the crystal. Such conditions are assumed to be fulfilled in cases of coated solid films and self-assembled monolayers.

The pressure dependence of frequency, AFP, increases with increasing pressure linearly, as shown by Stock-bridge[32- for gases up to 15 psi. Susse[33- described a similar relationship for liquids up to 1.5 x 104 psi. Thus AFP can be written as:

where a is the proportionality constant and Cp is the pressure sensitivity of QCM crystal, both of which are independent of the type of fluid in contact with the crystal.

The viscosity and density contribution, AFZ, describes the interaction of the vibrating crystal with a Newtonian viscous fluid. The interaction leads to an additional loading of the crystal, causing a decrease in frequency. AFZ is expressed to be proportional to the square root of the product of viscosity and density of the surrounding fluid:[32,34,35]

where pf and zf are the absolute density and viscosity of the fluid, respectively.

Fig. 3 Schematic view of a piezoelectric QCM crystal (only one side shown). A typical 5-MHz QCM from International Crystal Manufacturing consists of a thin quartz crystal (0.85 cm diameter) sputtered with a metal electrode (0.35 cm diameter) on each side. Both sides should be exposed to scCO2 because of high pressure.

Fig. 4 Schematic view of an experimental setup of QCM measurement system in scCO2.

Roughness Effect

A common feature of the approaches to QCM theory as reviewed by Thompson et al.[27- is the neglect of microscopic properties of interfaces and surface rough-ness.[36] This leads to deviations of most experimental frequency shift data from the predictions by these approaches. Buttry and Ward[23] and Schumacher et al.[37] observed that up to 80% of the observed frequency shifts for a crystal in contact with a liquid could be attributed to roughness effects.

As the microscopic properties of crystal-fluid interfaces change with the surface morphology, a predictive analytical expression for the roughness contribution to frequency, AFr, is not available. Urbakh and Dai- khin[36,38,39- formulated a model for surface roughness, assuming that a rough surface can be characterized by the average height (h), lateral length (a), and distance (l) between the inhomogeneities of the surface (Fig. 5). They incorporated this model into a framework of perturbation theory [36,38- and derived a general relationship for AFr as:

where C is a scaling function, related to three dimen-sionless factors, a/d, a/L, and h/a; d is the decay length of fluid velocities,

Table 2 Comparison of two microweighing methods

Characteristics	Gravimetric: MSB[21]	Piezoelectric: QCM[24]
Mass sensitivity	10- 5-10- 6g[13]	<10- 9g
Time resolution of	5 x 10- 2 sec[13] (need fine damping control system)	<10- 3 sec
response
Measuring variables	Gravity	Frequency and/or impedance
Calculations	Simple	Simple
Construction	Complex, especially the designing of the	Very simple
	magnetic coupling and fine damping control system
Size	Medium size when comparing with the QCM	Miniature size (0.5-2.5 cm diameter)
Calibration	Required to correct buoyancy	Not necessary[25]
Cost	Expensive	Cheap (<$30 a QCM crystal)a
Operation conditions	Mainly static;[13] extreme conditions	Both static and dynamic; extreme conditions
Applications	Mainly for processes and chemistries in	For processes and chemistries both in
	bulk phases	bulk phases and at thin films

In particular, if one assumes a slowly varying roughness (h/a ^ 1 and h/d ^ 1) for the crystal surface with a limit of a/d ^ 1or a/d ^ 1, the scaling function C is proportional to the ratio a/d.[36] Reformulating Eq. 5 yields:

where Cr= Cd is defined as the frequency-roughness correlation factor. This factor is only a function of surface roughness (h and a), provided that the assumptions above are fully established. Otherwise, Cr should be additionally viewed as a weak function of d.