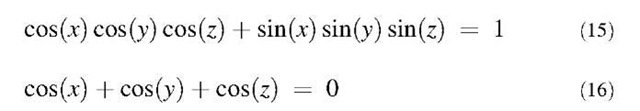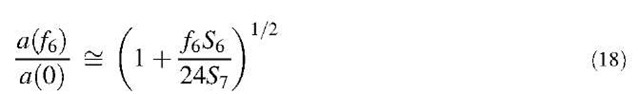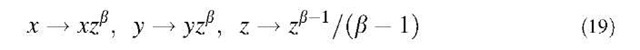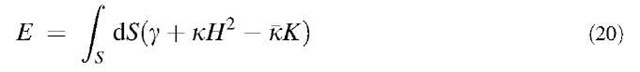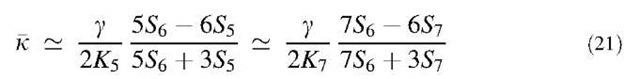Fullerenes: Topology and Structure Part 2 (Nanotechnology)

Nanotubes

A single-wall carbon nanotube can be constructed by rolling up a portion of a graphite sheet into a cylinder so as to bring an atomic site in the unit cell (L,M) of the graphite sheet to coincide with its equivalent site in the origin unit cell (0,0) (Fig. 4a). The structure of the nanotube is entirely defined by the pair of integer numbers (L,M). The diameter is given by.[60,61]

On pure geometrical grounds, the smallest open-ended nanotube is (3,0); however, with the requirement of end capping with six pentagons on each side, the smallest possible nanotube is (5,0) with a diameter of about 0.39 nm.

Nanotubes are classified into three types depending on the indices (L,M) (Fig. 4b-d): parallel nanotubes, with indices (L,0) or (0,M), where one third of the interatomic bonds is parallel to the nanotube axis; perpendicular nanotubes, with indices (L,L), where one third of the interatomic bonds is normal to the nanotube axis; and chiral nanotubes with either L > M >0 (right-handed) or M > L > 0 (left-handed).

From the symmetry point of view, the nanotube axis is a rotation axis of order L for both parallel (L,0) and perpendicular (L,L) nanotubes, whereas chiral nano-tubes have a screw axis. In the direction parallel to the axis, nanotubes are periodic with a period of 3r0 for the parallel type, V’3r0 for the perpendicular type and pdLM/ V3D(L, M) for the chiral type, where D(L,M) is the greatest common divisor of L and M. Thus for prime pairs, for which D(L,M)=1, the period along the axis is 1/V3 times the circumference.

Multiple-wall nanotubes grow by sequential addition of layers on an original single-wall nanotube. The interlayer distance is constant and is about 0.34 nm, with a tolerance that keeps, for energetic reasons, within about 1%. Thus the diameters of a multiwall nanotube with the concentric nanotubes labeled in the outward direction by n =1, 2, 3, … are given by

It turns out that each layer has indices (L’,M’) that differ from the indices (L,M) of the template (n =1) layer, their values being those that better simultaneously fulfill Eqs. 12 and 13 within a 1% tolerance (Fig. 5).

Apart from caps, which contain 12 pentagons each, ideal straight nanotubes are exclusively made of hexagonal rings as in the graphite sheet, with a good conjugation among interatomic bonds. However, as explained above, nanotubes can be bent with the addition of pentagon-heptagon pairs that introduce pairs of disclinations of opposite sign. In particular, an open-ended nanotube can be closed on itself to give a toroidal shape. Ring-shaped and even coiled nanotubes have been experimentally observed.[17,62]

Fig. 5 A multiwall nanotube is grown around an initial single-wall (9,2) nanotube of circumference C1 by the addition of further layers of circumferences C2 = Cj + 2p (0.34 nm), C3 = C2 + 2p (0.34 nm), etc. The indices of second, third, etc. layers are those that better match the respective radii with some interatomic distance: (15,8) and (19,16) in the present example.

Fig. 6 Illustration of the simplest topological defect in a nanotube originating from the rotation of the AB bond into A’B’. This operation, known as Stone-Wales transformation, reduces by one the edge number of polygons having AB in common and increases by one the edge number of the two adjacent polygons.

Nonideal nanotubes may have a variety of defects as in ordinary graphite. Of special interest here are the topological defects in which some hexagons are replaced by other polygons preserving the threefold coordination at each atom. Since the connectivity must not change, the number fjd of polygons replacing hexagons in each defect must fulfill the equation

as a consequence of Eq. 7. The simplest topological defect, which can be entirely accommodated within a 14-membered ring with no alteration outside, is constituted by two pentagon-heptagon pairs f5d =f7d=2) and is generated by the so-called Stone-Wales transformation (Fig. 6).

Periodic Schwarzites

The fourth form of sp2 (graphite-like) carbon, which we have called schwarzite, may be defined on a pure topological basis as a graphene with a negative average Gauss curvature (w < 0), unlike fullerenes and capped nanotubes, having w >0, and graphite, open and toroidal tubulenes, having w = 0. Any periodic surface with a periodicity in two or three space directions has a unit cell that can be closed by the periodic boundary conditions with two or three handles, respectively, and therefore the average Gauss curvature is always negative. As proved in ”Topology vs. Total Energy and Growth Processes,” the highest stability of a graphene with a negative w occurs for a shape corresponding to a minimal surface, namely when the principal radii fulfil the condition R1 = — R2 everywhere, or equivalently the mean curvature H vanishes at any point of the surface. Among the possible shapes of minimal surfaces, special attention has been given to branched tubular structures, as an obvious generalization of nanotubes,[30] which form two disjoint labyrinths, one complementary to the other. For this special feature, periodic schwarzites have been pictorially termed as the plumber’s nightmares.[30]

Periodic schwarzites are generated by covalent connections of identical units (elements). The unit cell may contain one or more such elements. The centers of the elements can be viewed as the nodes of a corresponding dual lattice. One of the two labyrinths, assumed as the internal one, contains the dual lattice. The dual lattice with the four-coordinated diamond structure defines an important class of cubic schwarzites, with two elements per unit cell (bielemental schwarzites). They are tessellations of a D-type minimal surface[28] (Fig. 7a). Monoele-mental cubic schwarzites with a sc, or bcc or fcc dual lattice are also possible, in principle, although the negative curvature of the elements becomes large and energetically unfavorable because of the increasing dual-lattice coordination (6, 8 and 12, respectively). However, sc(P-type) schwarzites (Fig. 7b) include a special class of structures known as polybenzenes, which have been predicted to be rather stable.[33]

Minimal surfaces can be analytically defined by means of the complex Weierstrass-Enneper representation.1-63,64-1 However, for visual representation purposes, a minimal three-periodic surface can indeed be sufficiently well approximated by a trigonometric expression corresponding to the lowest-order terms of a Fourier expansion. For example, D- and P-type surfaces are well described in the (x, y, z) space by respectively

 

In D-type schwarzites, each element is linked to four identical elements and therefore has four open terminations. Correspondingly, the unit cell, containing two elements, has six terminations. The closure procedure transforms a single element into a two-hole torus (kel=5), and the unit cell into a three-hole torus (kcell=7). Thus the Platonic tiling of a D type, according to Eq. 8, is obtained with either 12 heptagons or 6 octagons or 4 nonagons per element, and 28, 16, or 12 atoms per element, respectively. The corresponding numbers per unit cell are twice as much.

Each Platonic tiling is the zeroth element of an infinite series of larger schwarzites obtained by inserting in each element an arbitrary number f6>1) of hexagons. The number of atoms per element increases by two units for each additional hexagon (Eq. 6). Thus the D-type schwarz-ites with only heptagons and hexagons form a family of crystals with 2(28+ 2f6) atoms in the unit cell. However, only certain values of f6, given by

with l, n any integer > 0 and m=0, 1, are compatible with the tetrahedral symmetry and give a fcc crystal. Therefore the smallest member of this family is fcc-(C28)2 (l=n=m=0). The second member is fcc-(C36)2 (l=n=0 and m = 1) with 36 atoms per element and four hexagons in each element lying on the faces of the tetrahedron. The third member is fcc-(C40)2 (l =1 and m=n=0) with 40 atoms per element and six hexagons lying on the edges of the tetrahedron, etc. The respective elements are shown in Fig. 8a-c: While the elements offcc-(C36)2 andfcc-(C40)2 have a full tetrahedral point symmetry (Td) with six mirror planes, fcc-(C28)2 shows an intriguing chirality (T point group) that allows for two enantiomeric lattice forms. Fig. 9 depicts a portion of the fcc-(C36)2 lattice.[65]

Fig. 7 The unit cells of D-type (a) and P-type (b) schwarzites with a tessellation of hexagonal and heptagonal tiles. Schwarzites are three-periodical minimal surfaces. According to Euler’s theorem, heptagons (darker grey) must be 24 in the unit cell of both types, whatever is the number of hexagons (except 1). D-type schwarzites have the structure of a diamond lattice so that the unit cell can be split into two identical elements having 12 heptagons each, whereas P-type schwarzites have the structure of a simple cubic lattice. In principle, schwarzites can be associated to any kind of lattice, either periodic or amorphous (random schwarzites).

Fig. 8 The atomic structure of the elements of the smallest D-type schwarzites with a tetrahedral symmetry: (a) (C28)2 with 12 heptagons per element and no hexagon; (b) (C36)2 with 4 hexagons per element; (c) (C40)2 with 6 hexagons per element. The unit cell of D-type schwarzites contains two elements. Note that (C28)2 has a chirality that allows for two enantiomeric lattices, whereas (C36)2 and (C40)2 are achiral.

Isomeric forms of schwarzites are possible with rules similar to those applied to fullerenes, although no systematic analysis is presently available. Also, in this case, isomers with nonabutting heptagons are expected to be more stable. The smallest D-type schwarzite with nonabutting heptagons requires seven hexagons around each heptagon and three heptagons adjacent to each hexagon. This makes f6= 12(7/3) = 28 hexagons per element, corresponding to the lattice formula fcc-(C84)2. Indeed, this structure, analogous to C60 for being the smallest structure with nonabutting odd polygons, was theoretically predicted to be very stable.[30] The lattice constant a(f6) of the cubic cell for D-type fcc schwarzites with only heptagons and hexagons is approximately given by

where a(0)= 1.5 nm is the lattice constant of the Platonic member of the family and S7 = 3.634r72 is the area of the heptagons. It is a simple exercise to extend the above analysis to the family of schwarzites with only octagons and hexagons of both D and P types.

Fig. 9 The structure of the D-type schwarzite (C36)2 shows the distinct features of a face-centered cubic diamond lattice as seen along the (100) direction.

Amorphous sp2 Carbon

Among the various forms of amorphous graphite-like carbon, random schwarzites are of special interest here for their topological features as well as for the fact that they have been recently synthesized. The synthesis was achieved through SCBD in the presence of a metallor-ganic catalyst.[39] More information can be found in "Nanostructured Carbon, p. 000.” The SCBD experiments relied on a number of previous theoretical studies based on classical molecular dynamics of the aggregation process of carbon clusters in a gaseous phase[38] or during a cluster beam deposition on a substrate.[37] The aggregation process can be conveniently understood from a topological point of view, e.g., by following the evolution of the order of connection k as a function of time, namely as a function of the time step.

Two examples of such simulations, starting from different cluster distributions in the gas phase, are displayed in Fig. 10. The insets show the initial distributions of carbon clusters and the aggregation obtained at the end of the molecular dynamics simulations and after different changes of temperature.[38] Although the condensed phases obtained at the end of the simulation look qualitatively similar, the evolution of k follows different behaviors. In both cases, the connectivity, after large oscillations, becomes stabilized at a limit value klim, which is 3 for the aggregation of carbon dimers, or 5 for the aggregation of larger clusters. The first value corresponds to a graphitic layer (or open nanotube); the second value corresponds to a schwarzite. These structures can be better visualized by periodically repeating, in three dimensions, the cubic simulation cells shown in Fig. 10. The clear distinction between two regimes, with either an oscillating or a constant connectivity, has been viewed as the topological definition of an ill-condensed and a well-condensed phase, respectively. However, a constant value of k does not mean that the system does not evolve any more. However, the interatomic bonds keep breaking and reforming in a way that the connectivity remains constant. In fact, any change of k would require the sudden creation/annihilation of a fixed number of pentagons/heptagons, as a consequence of Euler’s theorem, and this has a substantial cost in terms of free energy. In principle, the evolution at constant k=3, 5 may gradually transform the above disordered structures into an ideal graphite layer (or an open-ended nanotube) or an ideal schwarzite, respectively.

Fig. 10 Simulations by classical molecular dynamics of the condensation process of carbon clusters of various sizes (a) or carbon dimers (c) into a connected graphene structure (b,d). The final condensation temperature is 3500 K. The time evolution, expressed in time steps of 0.7 fsec, of the order of connection k, allows to distinguish between ill-condensed and well-condensed matter, according to whether the connectivity oscillates or is stable. While a distribution of clusters including fullerene fragments leads to a connectivity corresponding to a schwarzite structure, the dimer gas condenses into graphite (or open nanotube) sheets. The simulation cells shown in a-d should be periodically repeated in three dimensions.

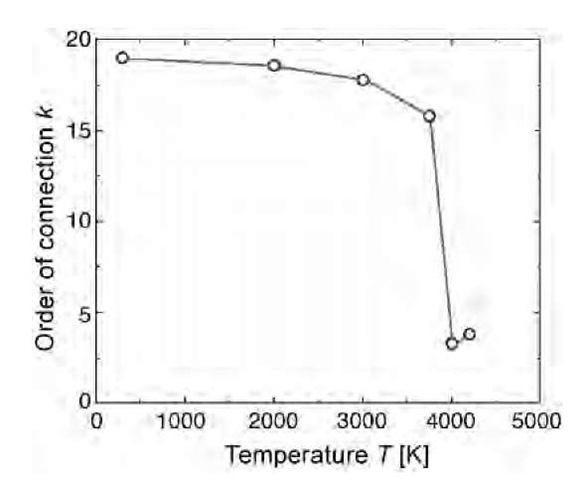
These examples show that the topological connectivity is a useful parameter for characterizing and monitoring the evolution of a condensed amorphous phase. Another application of this concept is illustrated in Fig. 11 where the thermal dissociation of the D-type schwarzite fcc-(C36)2 lattice is signaled by the sudden drop at Tc=3800 K of the order of connection k from 19, corresponding to eight elements within the cubic simulation cell, to 3, corresponding to a graphite sheet.[65] Thus the topological analysis reveals that transition at Tc corresponds to a graphitization process. This example shows that the order of connection can provide a sort of order parameter and a useful topological picture of a structural phase change.

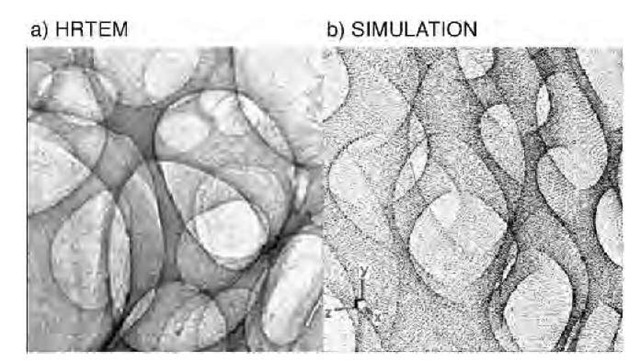
Series of high-resolution transmission electron microscope (HRTEM) images of this material, such as the one reproduced in Fig. 12a, suggested a novel form of nano-structured carbon consisting of three-dimensional, fully connected sp2 networks. This form of carbon seemingly consists of multiply connected graphene sheets forming a spongy structure with meso- and macroporosity, and appears to be fully covalent in three dimensions, which ensures a certain robustness as compared to fullerite and nanotube bundles, which are held together by van der Waals forces. An atomic force microscopy (AFM) analysis indicated that SCBD carbon films grow in a fractal self-affine structure[66-68] characterized by a growth exponent b of the order of 0.5.

In general, the reconstruction of the detailed three-dimensional structure is not possible from HRTEM images, but a useful comparison can be made with simulated images originating from the projection of a model analytical surface with suitable topological requisites. To simulate extended regions of the observed graphene surfaces as they appear in HRTEM images, analytical surfaces have been generated by applying a self-affine distortion along a given axis z, assumed as the growth direction, to the approximate Eqs. 15 and 16 for D-type or P-type three-periodic schwarzites through the coordinate transformation

where the coordinates x, y, z are in units of a conventional length ao= 1 nm and b=0.5. The direct comparison of the HRTEM images with the simulated ones (Fig. 12b) gives a convincing evidence that the observed SCBD spongy carbon can be ascribed to a random schwarzite, more precisely a form of fractal self-affine schwarzite.

Fig. 11 Thermal evolution of the D-type schwarzite (C36)2 as monitored by the connectivity for the simulation cell of Fig. 8. By heating up to 3700 K, the connectivity shows a small decrease as a result of a random break of bonds; but suddenly above that temperature, the connectivity drops to a small value, which is indicative of a transition leading to graphitization.

Fig. 12 (a) A high-resolution transmission electron microscope (HRTEM) image of random schwarzite obtained by supersonic cluster beam deposition compared with (b) an image simulation constructed through a self-affine distortion of an analytical expression for a P-type minimal surface.

TOPOLOGY VS. TOTAL ENERGY AND GROWTH PROCESSES

It has been shown[69] that the total energy of a curved single-walled graphene can be written in the form proposed by Helfrich for membranes and foams.[70-72]

where S is the (portion of the) surface which the total energy refers to and g=2.82 eV/A2 is the energy for a unitary flat surface (a graphite sheet)[61] The constants k and k are two elastic constants associated with cylindrical and elliptical/hyperbolic deformations of the surface, respectively. Density functional calculations in the local density approximation for nanotubes of variable radius R [where H =1/(2R) and K =0][73] and C60 (where H =1/R and K=1/R2)[61] permit to extract the values k = 3.1 eV and k = 1.7 eV. Consistently, a value of k = 1.5 eV can be obtained from the available calculations of the cohesive energy of schwarzites[28,30,42,65] by means of the Gauss-Bonnet theorem (Eq. 2). This shows that the above Helfrich’s form for the total energy approximately holds also for graphenes. The total energy expressed by Eq. 20 has the important property, if k is constant, that a minimal surface corresponds to a stable local minimum, because for k >0, the integral on H2 is always positive unless H =0, while the integral over K is, according to Gauss-Bonnet theorem, independent of any small continuous deformation of the surface. Thus graphenes taking the shape of a minimal surface, such as schwarzites, are stable forms, up to effects of the contour where k and k may change, as discussed below. If the negative disclinations yielding a negative Gauss curvature are exclusively because of heptagons, the number of disclinations Nd is fixed by the Euler characteristic as Nd=6(2 — w) independently of the length scale of the surface.[74] On the other hand, if the Gaussian surface energy density —UK is roughly assumed to be nonzero only at pentagons or heptagons, a local definition of kk is obtained as

where K5= 0.0808 A— 2 and K7 = — 0.0783 A— 2 are the Gaussian curvatures at a pentagon and a heptagon surrounded by five or seven hexagons, respectively.[27] With the polygon areas given above, Eq. 21 yields k = 2.1 eV for both pentagons and heptagons. The consistency of this value with that deduced from density-functional calculations for the various types of graph-enes confirms the validity of the Helfrich’s form of total energy for graphenes of any shape. The residual discrepancy of 0.4 eV may be ascribed to the crude approximations implied in Eq. 21, although this equation is useful because it relates kk to the actual size of the polygons generating the disclinations, hence to the local electronic structure. The values of k and k give general indications about whether the growth process of sp2 carbon preferentially leads to fullerenes, nanotubes, or schwarzites. In an incipient growth process from an initial radius R1 on the surface of a catalyst, the second principal radius R2 corresponding to a local energy minimum is obtained from Eqs. 3 and 20 as

The surface deformation energy densities for (spherical) fullerenes (Ri=R2 = R), nanotubes (Ri = R, R2!i), and schwarzites (R1 = — R2 = R) are (k — k)/R2, k/4R2 and kk/R2, respectively. Therefore, for any given R1, the values of k and k define three different topological domains: schwarzites are favored for k < 1/4k, nanotubes for 1/4k < k < 3/4k and fullerenes for k > 3/4k. When k « k/2, as found from density-functional calculations, nanotubes are more likely to occur. However, the local values of k and k either at the surface termination into vacuum, where the growth takes place by cluster addition, or at the contact with a catalyst where the growth process starts, may be quite different from the above values (which have been fitted to ideal close structures), and therefore other forms can be favored. The expected local changes in the electronic structure, e.g., a p bond-charge depletion or accretion, can substantially modify k. The fact that the growth of schwarzites supersedes that of nanotubes when metallorganic precursors are used[39] suggests that the charge redistribution produced by a catalyst, and the consequent change of the incipient k/k ratio, generally depend on the actual size (and shape) of catalyst nanoparticles. Once the growth has started as either a nanotube or a schwarzite, it is likely to proceed within the same topological domain. As mentioned above, simulations of the aggregation process of a fixed number of carbon clusters have shown that after the initial condensation process, the Euler-Poincare characteristic w stabilizes at a given value (for either the topology of a nanotube or a schwarzite, depending on the initial conditions) during all the subsequent morphological evolution. On the other hand, the growth of a fully connected schwarzite in the open space with a constant addition of atoms results in a progressive branching and joining of schwarzitic elements with an increase in connectivity and a corresponding stepwise increase Aw of w. The process leading to an increase in connectivity is actually favored if the corresponding total energy increase —2pkAw is overcompensated by the total energy decrease associated with the reduction in the free contour length. The geometrical constraints on the surface derivatives associated with the minimality conditions and topology (via Gauss-Bonnet theorem) lead to apparently well organized, albeit amorphous structures, through a fairly deterministic, low-entropy process.

CONCLUSION

Fullerenes, nanotubes, and schwarzites, when considered from the topological point of view, provide a paradigmatic example of the close link between topology and various physical aspects, ranging from thermodynamic stability to electronic and transport properties. In the particular case of schwarzites, the surface minimality condition, implied by the Helfrich form for the total energy, leads to the far-reaching consequence that an extensive property E (for example, the total energy) is minimal if and only if a local (intensive) condition I (for example, a vanishing mean curvature) is fulfilled everywhere. If the kinetics of a growth process are such that condition I is fulfilled at any step, then the property E turns out to be automatically minimal at any stage of the process. In this case the evolution of the system occurs along the valley bottom of the energy landscape.

The intriguing similarity between graphenes and foams, based on the Helfrich form for the total energy, suggests the existence of a wider class of systems, where the calculation of the total energy can be reduced, through a variable transformation, to the calculation of a surface area. For all of them the search for the stability conditions can be reformulated in the well-established mathematical realm of minimal surfaces. Many complex chemical systems such as supramolecular structures, nanoporous materials, biomembranes, and many other objects which are crowding into the rapidly growing fields of nano-structures and mesoscopic physics are characterized by complicated, highly connected surfaces with a large specific area and a large surface-free energy. A challenging question is whether the morphology and the stability of each of these systems can be reduced to a problem of minimal surfaces and solved with the tools of differential geometry.