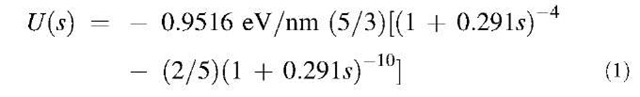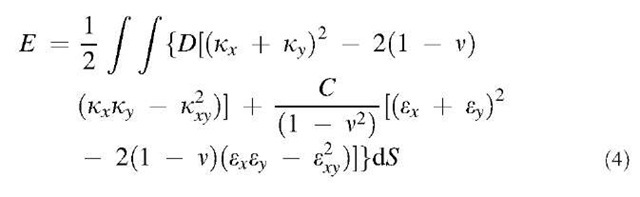INTRODUCTION
Supramolecular interactions are usually short-range (near contact) forces between the molecules, too weak to cause the intermolecular changes or bond formation between the particles. At the same time, their strength and range are sufficient to cause self-assembly of the molecular units or certain elastic deformations of these building blocks. Because of the weakness of supramolecular interactions, the resulting organization is sensitive to external conditions and ensures certain ease of transformations in response to external fields. Well known is a fascinating class of liquid crystals, whose ”liquid” aspect is exactly a result of relatively small energy of intermolecular forces. Nanoparticles and especially nanotubes offer a kind of building blocks that can be efficiently glued by weak supramolecular forces in a self-assembly process. In case of nanotubes, because of their hollow structure and large aspect ratio, same forces or interaction between them can cause deformations of bending, torsion, flattening poly-gonization, etc. In turn, the degree of such deformation can enhance (like in case of partial polygonization of nanotubes in the array bundles) supramolecular attraction or decrease it under other circumstances. Supramolecular behavior of nanotubes is therefore intrinsically coupled with their own mechanical properties which we will discuss in some detail.
Unique mechanical properties of carbon nanotubes indirectly lead to unusual role of the forces between them. These supramolecular interactions are normally weak and, for most molecular species, are easily overcome by thermal agitation. However, they turn out to be significant in case of nanotubes, building up very strong attractive potentials over the extensive aligned contacts 0.5 eV/ nm). The general aspects and issues of supramolecular mechanics are discussed, including an overview of the mechanical properties of nanotubes, especially linear elastic parameters and their relation with persistence length, nonlinear elastic instabilities, and buckling. Furthermore, inelastic relaxation, yield strength, and fracture mechanisms, including their kinetic theory, are also discussed. A discussion of theoretical and computational studies is supplemented by brief summaries of experimental results for the entire range of the deformation amplitudes. Atomistic scenarios of ”strong” supramo-lecular interactions, when polymerization and coalescence welding occur, are also discussed because of their significance in potential applications.
OVERVIEW
Nanomechanics is generally distinguished from the well-established dynamics of molecules in that it relies on the heuristics and methods of mechanical engineering and structural mechanics. It deals with objects of distinct shape and function: rods, beams, shells, plates, membranes, etc. At the same time, because of the small length scale, nanomechanics also relies on physics of interatomic and molecular forces, quantum chemistry, solid state theory, and statistical thermodynamics. With these come a variety of numerical and computational methods (molecular dynamics, Monte Carlo simulations, classical empirical interatomic potentials, tight-binding approximation, density functional theory, etc.). This cross-disciplinary aspect makes this area both complex and exciting for research and education.
Among the numerous subjects of nanomechanics research (tips, contact junctions, pores, whiskers, etc.), carbon nanotubes (CNTs)[1] have earned a spotlight (see Ref. [2] for a popular review). Their atomically precise structure, elongated and hollow, an effective absence of a surface (which is no different than the bulk, at least for the single-walled cylinders, SWNTs), and superlative cova-lent bond strength are among the traits that put CNTs in the focus of nanomechanics. Discussion of numerous other objects as well as details of the multiscale methods involved in nanomechanics (for example, see recent monograph[3]) is far beyond the scope of this article.
It is noteworthy that the term resilient has been first applied not to nanotubes, but to smaller fullerene cages, in the study of high-energy collisions of C60, C70, and C84 bouncing from a solid wall of H-terminated diamond. The absence of any fragmentation or other irreversible atomic rearrangement in the rebounding cages was somewhat surprising and indicated the ability of fullerenes to sustain great elastic distortion. The very same property of resilience becomes more significant in case of carbon nano-tubes because their elongated shape, with the aspect ratio close to a thousand, makes the mechanical properties especially interesting and important because of potential structural applications. An accurate simulation (with realistic interatomic and van der Waals forces) in Fig. 1[4] vividly illustrates the appeal of CNTs as a nanomechani-cal object: well-defined cylindrical shape, compliance to external forces, and an expected type of response qualitatively analogous to a common macroscopic behavior places these objects between molecular chemical physics, elasticity theory, and mechanical engineering.
The utility of nanotubes as elements in nanoscale devices or composite materials remains a powerful motivation for the research in this area. While the feasibility of the practical realization of these applications is currently unknown, another incentive comes from the fundamental materials physics. There is an interesting duality in the nanotubes. Carbon nanotubes possess simultaneously molecular size and morphology as well as sufficient trans-lational symmetry to perform as very small (nano-) crystals with well-defined primitive cell, surface, possibility of transport, etc. Moreover, in many respects, they can be studied as well defined as engineering structures and many properties can be discussed in traditional terms of moduli, stiffness or compliance, or geometric size and shape. The mesoscopic dimensions (a nanometer diameter) combined with the regular, almost translation-invariant morphology along the micrometer lengths (unlike other polymers, usually coiled) make nanotubes a unique and attractive object of study.
Fig. 1 Simulations of the axial and radial deformation of nanotubes. (a) Axial deformation resulting from the crossing of two (10,10) nanotubes. (b) Perspective close-up of the same crossing showing that both tubes are deformed near the contact region. (c) Computed radial deformations of single-wall nanotubes adsorbed on graphite.
In the following, ”Linear Elastic Properties” discusses theoretical linear elasticity and results for the elastic moduli, compared wherever possible with the experimental data. In ”Van der Waals Interactions,” the weak supramolecular interactions are quantified in the form of van der Waals force potential, and the large-scale mechanical deformations of nanotubes caused by their attraction to each other are outlined. The nonlinear elastic behavior, buckling instabilities, and shell model are presented in ”Supramolecular Morphology Changes Within Elastic Shell Model,” with mentioning of experimental evidence parallel to theoretical results. Yield and failure mechanisms in tensile load are presented in ”Failure and Relaxation Mechanisms,” with the emphasis on the combined dislocation theory and computational approach. More recent results of kinetic theory of fracture and strength evaluation in application to CNTs are briefly presented in ”Kinetic Approach to Strength-Failure Evaluation”; fast molecular tension tests are recalled in the context of kinetic theory. ”Coalescence of Nanotubes as a Reversed Failure” presents some of the more recent result on CNT coalescence welding, a process essentially reverse to fracture. In ”Tensegrity at Supramolecular Scale,” we also briefly discuss the concept of tensegrity and how it might be implemented in nanoscale by combining mechanically stiff and flexible supramolecular units. Throughout the discussions, we do not attempt to provide a comprehensive review of broad activities in the field. Broader or a more comprehensive discussion can be found in other relatively recent reviews by the author.[2,5]
LINEAR ELASTIC PROPERTIES
Numerous theoretical calculations are dedicated to linear elastic properties when displacements (strain) are proportional to forces (stress). We recently revisited[6] this issue to compare within the same method the elasticity of three different materials: pure carbon (C), boron nitride (BN), and fluorinated carbon (C2F). Because of obvious uncertainty in definition of a nanotube ”cross section,” the results should be represented by the values of in-plane stiffness, C (J/m2). The values computed with Gaussian-based density functional theory are C=345, 271, and 328 N/m for C, BN, and C2F, respectively. These values in ab initio calculations are almost independent of nano-tube diameter and chirality [consistent with the isotropic elasticity of a hexagonal two-dimensional (2-D) lattice], somewhat in contrast to previous reports based on tight binding or classical empirical approximations. Notably, substantial fluorination causes almost no change in the in-plane stiffness because the bonding involves mainly p-system while the stiffness is largely a result of in-plane ct-system. For ”material” property assessments, the values of bulk moduli (based on a graphite-type 0.34-nm spacing of layers) yield 1029, 810, and 979 GPa—all very high. Knowing the elastic shell parameter C immediately leads to accurate calculation of a nanotube beam-bending stiffness K (proportional to the cube of diameter, – d3) as discussed later in ”Van der Waals Interactions” and ”Coalescence of Nanotubes as a Reversed Failure.” It also allowed us to compute vibration frequencies of the tubules, e.g., symmetric breathing mode frequency, f— 1/d,[6] detectable in Raman spectroscopy.
An unexpected feature discovered in the course of that study[6] is the localized strain induced by the attachment of fluorine. This shifts the energy minimum of the C2F shell lattice from an ”unstrained” sheet toward the highly curved polygonal cylinders (for C2F composition of a near square shape, Fig. 2). Equilibrium free angle is — 72°.
Theoretical values agree reasonably well with experimental values of the Young’s modulus. It was first esti-mated[7] by measuring freestanding room-temperature vibrations in a transmission electron microscope (TEM). The motion of a vibrating cantilever is governed by the known fourth-order wave equation, ytttt= — (YI/pA)yxxxx, where A is the cross-sectional area and p is the density of the rod material. For a clamped rod, the boundary conditions are such that the function and its first derivative are zero at the origin and the second and third derivative are zero at the end of the rod. Thermal nanotube vibrations are essentially elastic, relaxed phonons in equilibrium with the environment; therefore the amplitude of vibration changes stochastically with time. The amplitude of those oscillations was defined by means of careful TEM observations of a number of CNTs and yields the values of moduli within a range near 1 TPa.
Fig. 2 Geometries of the polygonal fluorinated carbon tubes: (a) square F4-(10,10) and (b) pentagonal F5-(10,10).
Another way to probe the mechanical properties of nanotubes is to use the tip of an atomic force microscope (AFM) to bend an anchored CNT while simultaneously recording the force exerted by the tube as a function of the displacement from its equilibrium position.[8] Obtained values also vary from sample to sample but generally are close to Y= 1 TPa. Similar values have been obtained in Ref. [9] with yet another accurate technique based on a resonant electrostatic deflection of a multiwall carbon nanotube under an external a.c. field. The detected decrease in stiffness must be related to the emergence of a different bending mode for the nanotube. In fact, this corresponds to a wavelike distortion buckling of the inner side of the CNT. Nonlinear behavior is discussed in more detail in the next section. Although experimental data on elastic modulus are not very uniform, it corresponds to the values of in-plane rigidity C =340-440 N/m to the values Y =1.0-1.3 GPa for multiwall tubules and to Y =4C/ d =(1.36-1.76) TPa nm/d for SWNTs of diameter d.
VAN DER WAALS INTERACTIONS
Supramolecular interactions between the SWNTs are mainly because of van der Waals forces (VdW), except special situations when local charge or covalently bonded functional group introduce additional electrostatic fields. Van der Waals forces play also an important role in the interaction of the nanotubes with the substrata. The different shells of a MWNT (multiwall nanotube) interact primarily by van der Waals forces; single-wall tubes form ropes for the same reason.
An interesting manifestation of van der Waals interactions involves the self-interaction between two segments of the same single-wall CNT to produce a closed ring (loop).[10] Single-walled nanotube rings were first observed in trace amounts in the products of laser ablation of graphite and assigned a toroidal structure. More recently, rings of SWNTs were synthesized with large yields (— 50%) from straight nanotube segments. These rings were shown to be loops and not tori.[10] The synthesis involves the irradiation of raw SWNTs in a sulfuric acid-hydrogen peroxide solution by ultrasound. This treatment both etches the CNTs, shortening their length to about 3-4 mm, and induces ring formation.
Fundamentally, van der Waals attraction between the CNT is a result of dispersion forces, i.e., electrostatic dipole-to-dipole interaction (which gives V~ 1/r3 dependence of potential energy), and because the dipoles are mutually induced excited states, this actually yields nonzero effect only in the second-order perturbation theory, an always negative shift in potential energy f/2)–V2–1/r6.
For nanotubes and other carbon-cage structures, the van der Waals energy can be obtained from a universal graphitic potential[11] and for (10,10) tubes is
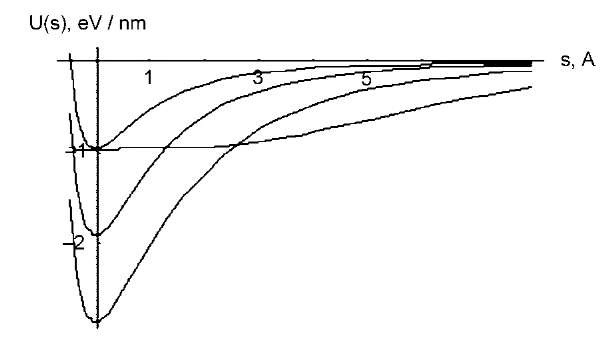
Equilibrium point s=0 corresponds to intercenter distance 1.67 nm that is wall-to-wall distance 0.315 nm, with the potential well depth about 0.95 eV/nm. This value is equivalent to energy of 0.04 eV per each pair of C-atoms facing across the van der Waals spacing, or near 0.9 kcal/ mol (e.g., of inserted spacer group that would push the nanotubes off the energy-minimum position). Although significant, this attraction energy decays fast with the nanotube separation: to the half of the value at only 1 A from equilibrium and almost vanishes at 3-5 A, as Fig. 3 shows.
The formation of coils by CNTs is particularly intriguing. While coils of biomolecules and polymers are well-known structures, they are stabilized by a number of interactions that include hydrogen bonds and ionic interactions. On the other hand, the formation of nanotube coils is surprising given the high flexural rigidity (K = Young’s modulus times areal moment of inertia) of CNTs and the fact that CNT coils can only be stabilized by van der Waals forces. However, estimates based on continuum mechanics show that, in fact, it is easy to compensate for the strain energy induced by the coiling process through the strong adhesion between tube segments in the coil. Details of this analysis can be found in the original reports[10] or in our recent review.[5] Here we will outline briefly a different and more common situation where the competition of elastic energy and the intertubular linkage is important. Following our recent work,[12] we will discuss the connection between the nanomechanics of CNTs and their random curling in a suspension or a raw synthesized material of bucky paper.
Fig. 3 Van der Waals energy per unit length is shown as function of displacement from equilibrium. From top down, three lines correspond to the tube deflecting from a contact with one, a pair, or a triplet of others; shallow plot corresponds to deflection in tangential direction.
Single-walled nanotubes are often compared with polymer chains as having very high rigidity and therefore large persistence length. To quantify this argument, we note that a defectless CNT has almost no static flexing, although 5/7 defects, for example, introduce small kink angle 5-15° and could cause some static curvature, but their energies are high and concentration is usually negligible. Only dynamic elastic flexibility should be considered. If u(s) is a unit direction vector tangent to the CNT at contour length point s, and the bending stiffness is K, then statistical probability of certain shape u(s) is
Here persistence length is L =(K/kbT). For a (10,10) SWNT of radius R=0.7 nm and the effective wall thickness h=0.09 nm (see ”Linear Elastic Properties” and ”Van Der Waals Interactions”), the bending stiffness is very close to K= pCR3 (C =345 N/m is the in-plane stiffness, based on ab initio calculations). Persistence length at room temperature therefore is Lj[(10,10), 293 K]~0.1 mm, in the macroscopic range much greater than for most polymer molecules. The result can be generalized for a single SWNT of radius R,
or N times more for a bundle of N tubes (assuming additive stiffness for the case of weak lateral cohesion of the constituent SWNTs). For example, for a smallest close packed bundle of seven (one surrounded by six neighbors), this yields L7=1 mm. Such incoherent bundle and a solid-coherent bundle with perfect lateral adhesion provide the lower and upper limits for the persistence length, NLj<Ln<N2Lj. Remarkably, these calculations show that the true thermodynamic persistence length of small CNT bundles or even an individual SWNT is in the macroscopic range from a fraction of a millimeter and greater. This means that highly curved structures often observed in bucky-paper mats (Fig. 4) are attributed not to thermo-dynamic fluctuations, but rather to residual mechanical forces preventing these coils from unfolding. Elastic energy of a typical micron size (r — 1 mm) curl-arc is much greater than thermal, Ucurl — kbT(L/r)2»kbT.[12] At the same time, a force required to maintain this shape Fcurl—K/r2=N pN, several piconewtons, where N is the number of SWNTs in each bundle. This is much less than a force per single chemical bond (— 1 nN), and therefore any occasional lateral bonding between the tubules can be sufficient to prevent them from disentanglement.
Fig. 4 Raw-produced SWNTs often form ropes-bundles entangled bent into a rubbery structure called ”bucky paper.” The length scale of bends is much smaller than the persistence length for the constituent filaments. Shown here is such material produced by HiPco (high pressure CO) synthesis method.
SUPRAMOLECULAR MORPHOLOGY CHANGES WITHIN ELASTIC SHELL MODEL
Almost any molecular structure can sustain very large deformations, compared with the range common in macroscopic mechanics. A less obvious property of CNTs is that the specific features of large nonlinear strain can be understood and predicted in terms of continuum theories. One of the outstanding features of nanotubes is their hollow structure, built of atoms densely packed along a closed surface that defines the overall shape. This also manifests itself in dynamic properties of molecules, resembling so much the macroscopic objects of continuum elasticity known as shells. Macroscopic shells and rods have long been of interest: the first study dates back to Euler, who discovered the elastic instability. A rod subject to longitudinal compression remains straight but shortens by some fraction e, proportional to the force, until a critical value (the Euler force) is reached. It then becomes unstable and buckles sideways at e > ecr, while the force almost does not vary. For hollow tubules, there is also a possibility of local buckling in addition to buckling as a whole. Therefore more than one bifurcation can be observed, thus causing an overall nonlinear response to the large deforming forces (note that local mechanics of the constituent shells may well still remain within the elastic domain).
In nanomechanics, the theory of shells was first applied in our early analysis of buckling and since then serves a useful guide.[13-16] Its relevance for a covalent-bonded system of only a few atoms in diameter was far from being obvious. Molecular dynamics simulations seem better suited for objects that are small.
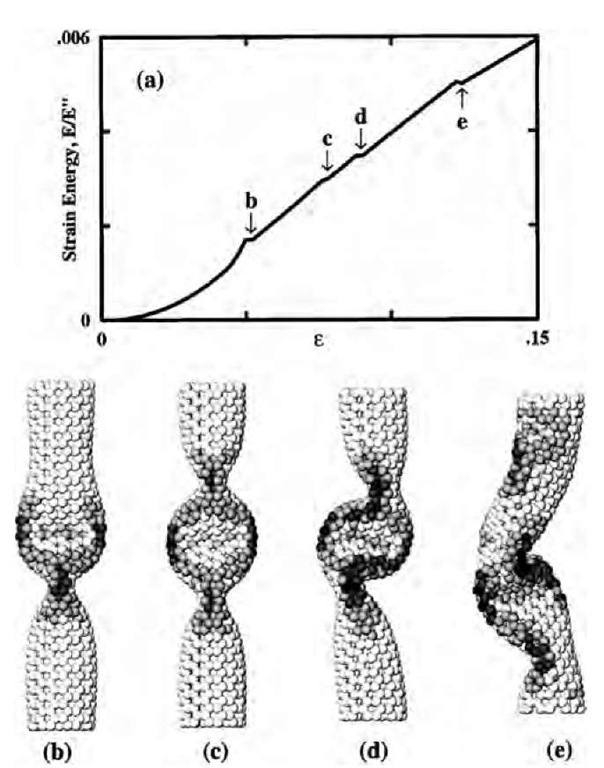
Fig. 5 Simulation of a (7,7) nanotube exposed to axial compression, L = 6 nm. The strain energy (a) displays four singularities corresponding to shape changes. At ec=0.05, the cylinder buckles into the pattern (b), displaying two identical flattenings—”fins” perpendicular to each other. Further increase of e enhances this pattern gradually until at e2=0.076, the tube switches to a three-fin pattern (c), which still possesses a straight axis. In a buckling sideways at e3=0.09, the flattenings serve as hinges, and only a plane of symmetry is preserved (d). At e4 = 0.13, an entirely squashed asymmetric configuration forms (e).
Fig. 5 shows a simulated nanotube exposed to axial compression. The atomic interaction was modeled by the Tersoff-Brenner potential, which reproduces the lattice constants and binding energies of graphite and diamond. The end atoms were shifted along the axis by small steps and the whole tube was relaxed by conjugate-gradient method while keeping the ends constrained. At small strains, the total energy (Fig. 5a) grows as E(e) = (1/2)E"e2. The presence of four singularities at higher strains was quite a striking feature and the patterns (b)-(e) illustrate the corresponding morphological changes. The shading indicates strain energy per atom, equally spaced from below 0.5 eV (brightest) to above 1.5 eV (darkest). The sequence of singularities in E(e) corresponds to a loss of molecular symmetry from DMh to S4, D2h, C2h, and Ci. This evolution of the molecular structure can be put in the framework of continuum elasticity.
The intrinsic symmetry of a graphite sheet is hexagonal, and the elastic properties of 2-D hexagonal structure are isotropic. A curved sheet can also be approximated by a uniform shell with only two elastic parameters: flexural rigidity D and its in-plane stiffness C. The energy of a shell is given by a surface integral of the quadratic form of local deformation,
where k is the curvature variation, e is the in-plane strain, and x and y are local coordinates. To adapt this formalism to a graphitic tubule, the values of D and C can be identified by comparison with the detailed ab initio and semiempirical studies of nanotube energetics at small strains. Indeed, the second derivative of total energy with respect to axial strain corresponds to the in-plane rigidity C (cf. ”Linear Elastic Properties”). Similarly, the strain energy as a function of tube diameter d corresponds to 2D/d2 in Eq. 4. Using recent ab initio calculations/ ] one obtains C =56 eV/atom=340 J/m2 and D =1.46 eV. The Poisson ratio v = 0.15 was extracted from a reduction of the diameter of a tube stretched in simulations. A similar value is obtained from experimental elastic constants of single crystal graphite. One can make a further step toward a more tangible picture of a tube as having wall thickness h and Young modulus Ys. Using the standard relations D=Yh3/12(1 – v2) and C = Ysh, one finds Ys=3.9 TPa and h=0.089 nm. With these parameters, linear stability analysis allows one to assess the nanotube behavior under strain.
Fig. 6 The critical strain levels for a continuous, 1-nm-wide shell tube as a function of its scaled length L/N. A buckling pattern (M,N) is defined by the number of halfwaves 2M and N in y and x directions, respectively, e.g., a (4,4)-pattern is shown in the inset. The effective moduli and thickness are fit to graph-ene.
To illustrate the efficiency of the shell model, consider briefly the case of imposed axial compression. A trial perturbation of a cylinder has a form of Fourier harmonics, with M azimuthal lobes and N halfwaves along the tube (Fig. 6 inset), i.e., sines and cosines of arguments 2My/d and Nnx/L. At a critical level of the imposed strain, ec(M,N), the energy variation (4.1) vanishes for this shape disturbance. The cylinder becomes unstable and lowers its energy by assuming an (M,N) pattern. For tubes of d =1 nm with the shell parameters identified above, the critical strain is shown in Fig. 6. According to these plots, for a tube with L>10 nm, the bifurcation is first attained for M =1, N =1. The tube preserves its circular cross section and buckles sideways as a whole; the critical strain is close to that for a simple rod,
or four times less for a tube with hinged (unclamped) ends. For a shorter tube, the situation is different. The lowest critical strain occurs for M=2 (and N> 1, see Fig. 6), with a few separated flattenings in directions perpendicular to each other, while the axis remains straight. For such a local buckling, in contrast to (4.2), the critical strain depends little on length and estimates to ec = 4^D/Cd-1 = (2/P3)(1 – v2)-1/2hd-1 in the so-called Lorenz limit. For a nanotube, one finds
Specifically, for the 1-nm-wide tube of length L=6 nm, the lowest critical strains occur for M =2 and N =2 or 3 (Fig. 6). This is in accord with the two- and three-fin patterns seen in Fig. 5b and c. Higher singularities cannot be quantified by the linear analysis, but they look like a sideways beam buckling, which at this stage becomes a nonuniform object.
Axially compressed tubes of greater length and/or tubes simulated with hinged ends (equivalent to a doubled length) first buckle sideways as a whole at a strain consistent with (5). After that, the compression at the ends results in bending and a local buckling inward. This illustrates the importance of the ”beam-bending” mode, the softest for a long molecule and most likely to attain significant amplitudes because of either thermal vibrations or environmental forces. In simulations of bending, a torque rather than force is applied at the ends and the bending angle 0 increases stepwise. While a notch in the energy plot can be mistaken for numerical noise, its derivative dE/d0 drops significantly. This unambiguously shows an increase in tube compliance—a signature of a buckling event. In bending, only one side of a tube is compressed and thus can buckle. Assuming that it buckles when its local strain, e=kd/2, where k is the local curvature, is close to that in axial compression, Eq. 6, we estimate the critical curvature as
In simulation of torsion, the increase of azimuthal angle f between the tube ends results in abrupt changes of energy and morphology.[13,14,17] In continuum model, the analysis based on Eq. 4 is similar to that outlined above, except that it involves skew harmonics of arguments such as Nnx/L±2My/d. For overall beam buckling (M =1),
and for the cylinder-helix flattening (M =2),
The latter should occur first for L < 140d5/2 nm, which is true for all tubes we simulated. However, in simulations, it occurs later than predicted by Eq. 9. The ends, kept circular in simulation, which is physically justifiable, by a presence of rigid caps on normally closed ends of a molecule, deter the thorough flattening necessary for the helix to form (unlike the local flattening in the case of an axial load).
Experimental evidence provides sufficient support to the notion of high resilience of SWNT. An early observation of noticeable flattening of the walls in a close contact of two MWNT has been attributed to van der Waals forces pressing the cylinders to each other.[18]
Collapsed forms of the nanotube (”nanoribbons”), also caused by van der Waals attraction, have been observed in experiment, and their stability can be explained by the competition between the van der Waals and elastic ener-gies.[19] Any additional torsional strain imposed on a tube in experimental environment also favors flattening[13,14] and facilitates the collapse. Graphically more striking evidence of resilience is provided by bent structures,[20] as well as the more detailed observations that actually stimulated our research in nanomechanics.[21] An accurate measurement with the atomic force microscope (AFM) tip detects the ”failure” of a multiwall tubule in bending,[8] which essentially represents nonlinear buckling on the compressive side of the bent tube. The estimated measured local stress is 15-28 GPa, very close to the calculated value.[22,23] Buckling and ripple of the outmost layers in a dynamic resonant bending has been directly observed and is responsible for the apparent softening of MWNT of larger diameters.[5,24]