INTRODUCTION
Graphite exhibits a three-dimensional (3-D) stacking ordering of large graphene layers (where an individual carbon layer in the honeycomb graphite lattice is called a graphene layer) of planar hexagonal networks of carbon atoms based on sp2 bonding. In contrast, carbons consist of randomly stacked defective and relatively small graphene sheets, which are termed turbostratic carbons (T-carbons). Furthermore, carbon nanotubes are seamless cylindrical forms of such graphene layers of nanometer-size diameter, consisting of single- or concentric mul-tilayers.[1-3] The diameter of the central hollow core is basically of fullerene size (around 1 nm), and the minimum size diameter that has been observed is 0.4 nm.[4] These carbon nanotubes are strongly related to 3-D-graphite or T-carbon when considering their large curvature (see Fig. 1). The nanotube curvature introduces some sp3 bonding into the sp2 planar bonding of the graphene sheet. Numerous unusual properties of carbon nanotubes arise from the sp2 graphene layers by imposing additional quantum confinement and topological constraints in the circumferential direction of the nanotubes. In this topic, carbon nanotubes are first reviewed in terms of their relevance to typical carbon and graphite materials and then are connected with other fibrous forms of carbon and graphite.
BASIC CONCEPTS FROM FIBERS TO NANOTUBES
As carbon nanotubes might be the ultimate 1D form of carbon, their structure and properties are closely related to those of other forms of carbon, especially to crystalline 3-D-graphite, T-carbons, and to their constituent 2D layers. Therefore several forms of conventional carbon materials should be mentioned in terms of their similarities and differences relative to a carbon nano-tube. Especially, a direct comparison should be made between typical 1D materials of carbon and graphite (carbon fibers), because the carbon fiber acts as a bridge between carbon nanotubes and conventional bulky carbon materials.
Carbon fibers were developed in the early 1960s and have given many breakthroughs to carbon science because of their unique fibrous morphology.[5,6] Therefore it is necessary to compare the structure and properties of carbon nanotubes with conventional carbon fibers exhibiting diameters around 10 ^m. Furthermore, there are also very important materials that can be related to both carbon nanotubes and carbon fibers. These are called the vapor-grown carbon fibers (VGCFs) synthesized directly by the catalytically assisted pyrolysis of hydro-carbons.[7-10] Vapor-grown carbon fibers have diameters ranging from 1 nm to 10 ^m, the thinner ones corresponding to carbon nanotubes and the thicker ones are similar to carbon fibers. It has been reported that the central core of a VGCF consists of a carbon nanotube.[11] Through precise control of the synthesis conditions, it is possible to produce carbon nanotubes and carbon fibers on a large scale. Both materials have been industrialized for different practical applications.1-12-1 Therefore the structures of carbon nanotubes and carbon fibers as well as VGCFs, in which the latter connects both typical materials, are strongly emphasized in this account. We will also show the similarities and differences of these 1D carbon materials.
BONDING NATURE OF CARBON ATOMS
Carbon is the sixth element in the periodic table and has the lowest atomic number of any of the elements in column IV. Each carbon atom has six electrons which occupy 1s2, 2s2, and 2p2 atomic orbitals. The 1s2 orbital contains two strongly bound core electrons. Four more weakly bound electrons occupy the 2s22p2 valence orbitals. In the crystalline phase, the valence electrons give rise to 2s, 2px, 2py, and 2pz orbitals, which are important in forming covalent bonds within carbon materials. Because the energy difference between the upper 2p energy levels and the lower 2s level in carbon is small compared to the binding energy of the chemical bonds, the electronic wave functions for these four electrons can readily mix with each other, thereby changing the occupation of the 2s and three 2p atomic orbitals, so as to enhance the binding energy of a C atom with its neighboring atoms. The general mixing of 2s and 2p atomic orbitals is called hybridization, whereas the mixing of a single 2s electron with one, two, or three 2p electrons is called spn hybridization with n =1, 2, 3.[13,14]
Fig. 1 Schematic diagram of an individual carbon layer in the honeycomb graphite lattice called a graphene layer, and how it can be rolled to form a carbon nanotube.
Thus three possible hybridizations occur in carbon: sp, sp2, and sp3, while other group IV elements, such as Si and Ge, exhibit primarily sp3 hybridization. Carbon differs from Si and Ge because carbon has no inner atomic orbitals, except for the spherical 1s orbitals, and the absence of nearby inner orbitals facilitates hybridizations involving only valence s and p orbitals for carbon. The various bonding states are connected with certain structural arrangements, so that sp bonding gives rise to a chain structure such as carbynes, sp2 bonding to planar structures such as graphene, and sp3 bonding to a tetrahedral structure such as diamond.
The carbon phase diagram (see Fig. 2) guided the historical synthesis of diamond in 1960 and has continued to inspire interest in novel forms of carbon, as they are discovered.[15,16] While sp2 bonded graphite is the ground-state phase of carbon under ambient conditions, at higher temperatures and pressures, sp3 bonded cubic diamond is stable. Other regions of the phase diagram show stability ranges for hexagonal diamond, hexagonal carbynes,[17,18] and liquid carbon.[19] The triple point of the graphite-diamond-liquid phase is located at 123 kbar and 4100 K. It is expected that a variety of novel p-electron carbon bulk phases still remain to be discovered and explored.
A carbon nanotube is a graphene sheet appropriately rolled into a cylinder of nanometer-size diameter.[2,3,20-23] The curvature of the nanotubes admixes a small amount of sp3 bonding so that the force constant (bonding) in the circumferential direction is slightly weaker than along the nanotube axis. Because the single-wall carbon nanotube (SWNT) is only one atom thick and has a small number of atoms around its circumference, only a few wave vectors are needed to describe the periodicity of the nanotubes. These constraints lead to quantum confinement of the wavefunctions in the radial and circumferential directions, with plane wave motion occurring only along the nanotube axis, corresponding to a large number or closely spaced allowed wave vectors. Thus although carbon nanotubes are related to a 2D graphene sheet, the tube curvature and the quantum confinement in the circumferential direction lead to a host of 1D properties that are different from those of a graphene sheet. As nanotubes can be rolled from a graphene sheet in many ways, there are numerous possible orientations of the hexagons on the nanotubes, although the basic shape of the carbon nanotube wall is a cylinder, where the two indices (n, m) that fully identify each carbon nanotube are [2 3 23] specified.[2,3,23] The rolling of a single graphene layer, which is a honeycomb network of carbon atoms, to form a carbon nanotube is well reviewed in many review papers and books." ] Carbon nanotubes (n, m) can be either metallic (n_m= 3q, q=0, 1, 2,…) or semiconducting (n_ m=3q±1, q=0, 1, 2,…), and likewise the individual constituents of multiwall nanotubes or single-wall nano-tube bundles can be metallic or semiconducting.[2,3,21]
These remarkable electronic properties follow from the electronic structure of 2D graphite under the constraints of quantum confinement in the circumferential direction.[2]
GRAPHITES AND DISORDERED CARBONS
The ideal crystal structure of graphite (Fig. 3a) consists of layers in which the carbon atoms are arranged in an open honeycomb network, such that the A and B atoms on consecutive layers are on top of one another, but the A’ atoms in one plane are over the hexagon centers of the adjacent layers, and similarly for the B’ atoms.[24] This give rise to an ABAB planar stacking arrangement (called Bernal stacking) shown in Fig. 3a, with an in-plane nearest neighbor distance aC-C of 1.421 A, an in-plane lattice constant ao of 2.456 A, a c-axis lattice constant co of 6.708 A, and an interplanar distance of 3.354 A. This structure is consistent with the D6h4 (P63/mmc) space group and has four atoms per unit cell.
Fig. 2 The phase diagram of carbon.[15] The diamond (Di) and graphite (Gr) phases are emphasized in this figure. Other phases shown in the diagram include hexagonal diamond and a high-temperature-high-pressure phase, denoted in the diagram by du Pont, meteorites, and shock-quench, which has not been studied in much detail and may be related to carbynes. Liquid carbon, which has been studied at low pressures and high temperatures, and an unexplored high-pressure phase, which may be metallic, are also indicated on the figure.
Another ordered graphite phase is rhombohedral graphite with ABC stacking of the graphene sheets; it has ao = 2.456 A (same as for Bernal-stacked hexagonal graphite), co=3(3.438)= 10.044 A, and space group D37 (R32).[24] When describing the ABC stacking of graphene sheets in the hexagonal structure, it is necessary to consider six atoms per unit cell, but if the rhombohedral description is used, only two atoms per unit cell are needed. Because the total energy for rhombohedral graphite differs only slightly from that of the more stable Bernal ABAB stacking (Table 1), graphite crystals tend to have stacking faults where ABC rhombohedral stacking is found admixed with the AB Bernal stacking for the ideal graphite crystal. Most of graphite crystals and natural graphite follow the hexagonal system, but, sometimes, natural graphite and artificial graphite heat-treated at high temperatures have been observed to include several percent of the rhombohe-dral system. Also, mechanical grinding and ball milling increase the rhombohedral component.
Stacking disorder tends to have little effect on the in-plane lattice constant largely because the in-plane C-C bond is very strong and the nearest-neighbor C-C spacing is very small. As has already been mentioned elsewhere, the C-C spacing in fullerenes and carbon nanotubes is very close to aC-C. Disorder does, however, have a significant effect on the interplanar spacing, because of the weak interplanar bonding based on the van der Waals force. One consequence of the small value of aC-C and the large value of the interplanar c-axis separation is that impurity species are unlikely to enter the in-plane lattice sites substitutionally, but rather impurities tend to occupy some interstitial positions between the layer planes as to form intercalation compounds.
Weak disorder results in stacking faults (meaning departure from the ABAB stacking order) and gives rise to a small increase in the interlayer distance. This increase is modest when ABC stacking faults are occasionally introduced. Greater disorder is introduced when the stacking become random or uncorrelated and departs from AB or ABC stacking. The greater the stacking disorder the greater the interlayer distance, until random stacking occurs. When the interlayer spacing reaches a value of about 3.44 A, the stacking of the individual graphene layers becomes uncorrelated. The resulting 2D honeycomb structure of uncorrelated graphene layers is called turbostratic carbon (see Fig. 3b).[24]
Fig. 3 Schematic diagrams exhibiting (a) a 3-D graphite lattice (b) a turbostratic structure,[24] and (c) a schematic structural model of the outer two layers for a multiwall carbon nanotube.[33] The inset in (a) depicts the A and B carbon sites denoted by open circles and the A’ and B’ sites by black circles. The in-plane lattice constant is denoted by a0, and the vectors of the unit cell in the direction a1, a2, and c are indicated. The nearest-neighbor carbon distance aC_C in graphite is 1.421 A.
Table 1 Cohesive energy per carbon atom for various carbon-related structures
|
Structure |
Cohesive energy (meV/atom) |
Ref. |
|
3-D graphite |
20.0 |
[25-27] |
|
Rhombohedral graphite |
19.9 |
[27] |
|
2D graphene sheet |
10.3 |
[25-27] |
|
Carbon nanotube |
9.76 |
[25] |
|
(based on C60) |
In both structures, the bonding force between adjacent carbon hexagonal networks is the van der Waals force. The degree of 3-D ordering or the stacking fidelity is defined in terms of the degree of graphitization (g) as a function of the interlayer spacing (d002), by the following equation,[28] where g is the probability to preserve 3-D stacking.
For interlayer spacings larger than 3.44 A, the probability of 3-D stacking is 0, and d002 = 3.354 A gives perfect 3-D graphite ordering with g =1. Between g=0^1, various forms of carbon materials exist as a function of heat treatment temperatures. For carbonaceous materials exhibiting a g value in the range between 0.5 and 1 when heat-treated up to 3000°C, these pristine carbons are called graphitizing or soft carbons.[29,30] In contrast, carbonaceous materials with lower g values, exhibiting a high resistance for graphitization, are so-called nongraphitizing or hard carbons.[29,30] These graphitization behaviors are strongly dependent on the microstructure of carbonaceous materials, where highly oriented small carbon networks (the smallest called a basic structural unit) generally determine the graphitizability. The chemical and physical properties, such as the electrical resistivity and mechanical strength, are largely affected by the graphitizing nature of a carbon. Therefore structural control of the pristine material, namely, the starting organic material, is very important for designing the desired performance of carbons and graphite.[31,32]
Fig. 4 Comparative study of transverse magnetoresistance at low temperature (as indicated in parenthesis) for highly oriented pyrolytic graphite (the dot-dashed curve),[34] typical mesophase-pitch-based carbon fibers heat treated at different temperatures (the solid curves),[13] vapor-grown carbon fibers (the dashed curve),[35] and multiwall carbon nanotubes (the dotted curve).[36] Vapor-grown carbon fibers exhibit a similar magnetoresistance behavior to that of multiwall carbon nanotubes.
The electronic structure of turbostratic graphite, a zero-gap semiconductor, is qualitatively different from that of ideal graphite, a semimetal with a small band overlap (0.04 eV). As the crystalline disorder is further increased and the in-plane ordering in the graphene sheets is reduced, the interlayer spacing also continues to increase. Such disorder further modifies the electronic properties of the ideal 2D graphite and introduces an effective energy gap.
Multiwall carbon nanotubes (MWNTs) relate closely to the layer stacking of graphite, insofar as the interlayer spacing is found to vary from 3.4 to 3.6 A between adjacent cylinders, possibly due to glide defects (see Fig. 3c).[33] Magnetoresistance measurements provide a highly sensitive measure of the degree of 3-D crystalline order using the following equation.
where p(B) and r(0) are the electrical resistivity with and without a magnetic field B, respectively. As shown in Fig. 4,[12,34-36] highly oriented pyrolytic graphite with the highest degree of structural perfection shows large positive transverse magnetoresistance, with smaller values of positive Ap/p0 [mesophase-pitch-based carbon fibers (MPCFs) at 3000°C] corresponding to more disordered graphite. As more disorder is introduced, the 3-D ordering disappears and the fibers assume 2D or turbostratic ordering, where there is no interlayer site correlation between adjacent graphene planes. The magnetoresistance for the turbostratic carbon is characteristically negative, with the magnitude of the negative magnetoresistance decreasing as the disorder increases. For the case of VGCFs heat treated at 2000°C[35] and multiwall carbon nanotubes,[36] the negative magnetoresistance strongly suggests that the stacking infidelity of the shells is quite similar to that of turbostratic graphite regarding their electronic properties along the tube axis (see the dotted curve in Fig. 4). The curvature of the coaxial layers, however, excludes the possibility of the AB or ABC stacking of the graphene layers, and in this sense, the stacking of layers in a MWNT is equivalent to turbostratic stacking (see Fig. 3c). As some interlayer site correlation between carbon atoms exists in nanotubes, especially regarding the direction of the nanotube axis, the interlayer stacking is not completely turbostratic. Also, for small-diameter carbon nanotubes, there is a limited number of possible nanotube diameters, and these depend also on the nanotube chirality, so that it is not in general possible to find a nested set of nanotubes which all have the same chirality and also show a close packing of cylindrical shells. Thus the electronic properties of multiwall carbon nanotubes have some differences and some similarities when compared with T-carbons.
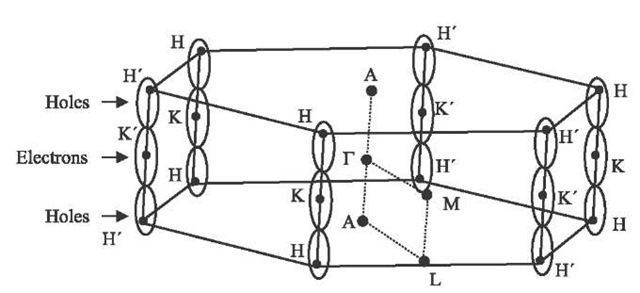
In order to describe the electronic and phonon dispersion relations of 3-D graphite, the Brillouin zone (see Fig. 5) is used.[3,13] As the in-plane nearest-neighbor distance in real space is much smaller than the interplanar separation, the Brillouin zone for graphite has a small length in reciprocal space along kz. As the interplanar correlation becomes less and less important, as in the case of turbostratic 2D graphene layers, the Brillouin zone is reduced to a sheet. The special point K at the Brillouin zone corner in 2D graphite is the location of the Fermi level, and of the symmetry-imposed degeneracy of the conduction and valence bands,[37] making 2D graphite a zero band gap semiconductor. The band structure model for graphite near the Fermi energy (EF) focuses on the electronic dispersion relations in the vicinity of the HKH and H’K'H’ edges of the Brillouin zone.
Fig. 5 Graphite Brillouin zone showing several high-symmetry points and a schematic version of the graphite electron and hole Fermi surfaces located along the HKH and H’K'H’ axes.
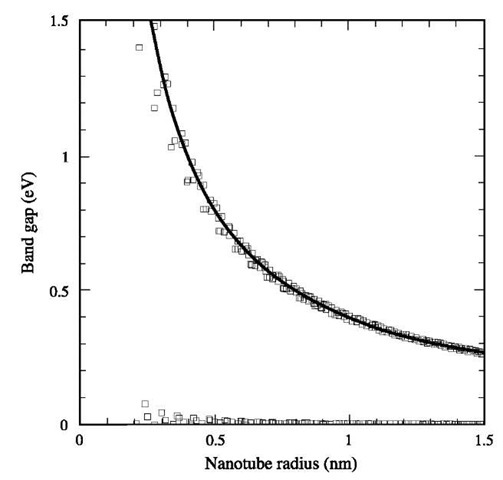
Fig. 6 Band gap as a function of nanotube radius calculated using an empirical tight-binding Hamiltonian.
MULTI- AND SINGLE-WALL CARBON NANOTUBES
Carbon nanotubes can be visualized as rolled sheets of graphene that are sometimes capped (by a fullerene-like hemisphere) on each end. They can be single-walled with diameters as small as about 0.4 nm, or multiwalled (2 to 30 concentric tubes positioned within one another) with outer diameters ranging from 5 to 100 nm. The constituent shells of MWNTs can possess many different helical structures, and variations in the radii and helical structures have been predicted to affect the nanotube’s electronic transport, which can vary from metallic to semiconduct-ing.[2,3] As shown in Fig. 6, the band gap estimated by an empirical tight-binding method as a function of nanotube radius suggests that as the nanotube’s diameter gets larger, thus decreasing the pronounced curvature of a graphene layer, the value of the band gap corresponds to that of graphene sheet.[38] Three typical structures of SWNT have been proposed (Fig. 7), and their structures have been confirmed by scanning tunneling microscopy (STM) and electron diffraction studies.[3,39,40] If the C60 molecule is bisected normal to a fivefold axis, the cap for an ”armchair” nanotube is formed, and if the C60 molecule is bisected normal to a threefold axis, the cap for a ”zigzag” nanotube is formed. In addition to the armchair and zigzag nanotubes, a large number of chiral carbon nanotubes can be formed with a screw axis along the axis of the nano-tube, which is terminated by a variety of ”hemispheri-cal”-like caps.
Fig. 7 Three typical structural models for SWNTs, where the nanotubes are related to rolling a graphene sheet into a cylinder.[2'3] Fullerene caps for the armchair and zigzag tubes are also indicated.
On the other hand, in MWNTs, no graphitic 3-D stacking is established, although an individual shell of the multilayers consists of perfect graphene sheets. Also, each tube has different and independent chirality, which might contribute to a larger inter-shell spacing than is found in graphite. These characteristic structures of SWNTs and MWNTs indicate that they are unique 1D materials with fascinating electronic and mechanical properties.
FIBROUS FORMS OF CARBON AND GRAPHITE
Carbon fibers represent an important class of graphite-related materials that are closely related to carbon nanotubes, with regard to structure and properties. Carbon fibers have been studied scientifically since the late 1950s and fabricated industrially since 1963. They are now becoming a technologically and commercially important material in the aerospace, construction, sports, electronic device, and automobile industries. The global carbon fiber market has now grown to about 12,500 tons/year of product, after 40 years of continuous R&D work.[41] Carbon fibers are defined as a filamentary form of carbon with an aspect ratio (length/diameter) greater than 100. Probably, the earliest documented carbon fibers are the bamboo-char filaments made by Edison for use in the first incandescent light bulb in 1880. With time, carbon fibers were replaced by the more robust tungsten filaments in light bulb applications, and, consequently, carbon fiber R&D vanished at that early time. But in the late 1950s, carbon fibers once again became important because of the aggressive demand from aerospace technology for the fabrication of lightweight, strong composite materials, in which carbon fibers are used as a reinforcement agent in conjunction with plastics, metals, ceramics, and bulk carbons. The specific strength (strength/weight) and specific modulus (stiffness/weight) of carbon fiber-reinforced composites demonstrate their importance as engineering materials, because of the high performance of their carbon fiber constituents.
Because the temperature and pressure necessary to prepare a carbon fiber from the liquid phase is at the triple point (T=4100 K, p =123 kbar, see Fig. 2), it would be almost impossible to prepare carbon fibers from the melt under industrial processing conditions. Carbon fibers are therefore prepared from organic precursors. This preparation is generally done in three steps, including stabilization of a precursor fiber in air (at ~ 300°C), carbonization at ~ 1100°C, and subsequent graphitization (above 2500°C). Fibers undergoing only the first two steps are commonly called ”carbon fibers,” while fibers undergoing all three steps are called ”graphite fibers.” Carbon fibers are generally used for their high strength, while graphite fibers are used for their high modulus.
Fig. 8 Model for graphite whiskers grown by the DC arc-discharge of graphite electrodes.[42] Whiskers were reported to have the carpet-rolling structure of graphite sheets and to have high mechanical strength and modulus along the fiber axis, similar to the ideal values of a graphene sheet.
Historically, Bacon’s graphite whisker (see Fig. 8) has demonstrated the highest mechanical properties of a carbon fiber (with regard to both strength and modulus), comparable to the ideal value for a graphite network.[42] Graphitic whiskers were grown under conditions near the triple point of graphite. Then, the structural model was proposed, in which the layers consisting of graphene sheets are wound around the axis as in rolling up a carpet. These whiskers were used as the performance target in the early stages of carbon fiber technology, although they have never been produced on a large scale.

![The phase diagram of carbon.[15] The diamond (Di) and graphite (Gr) phases are emphasized in this figure. Other phases shown in the diagram include hexagonal diamond and a high-temperature-high-pressure phase, denoted in the diagram by du Pont, meteorites, and shock-quench, which has not been studied in much detail and may be related to carbynes. Liquid carbon, which has been studied at low pressures and high temperatures, and an unexplored high-pressure phase, which may be metallic, are also indicated on the figure. The phase diagram of carbon.[15] The diamond (Di) and graphite (Gr) phases are emphasized in this figure. Other phases shown in the diagram include hexagonal diamond and a high-temperature-high-pressure phase, denoted in the diagram by du Pont, meteorites, and shock-quench, which has not been studied in much detail and may be related to carbynes. Liquid carbon, which has been studied at low pressures and high temperatures, and an unexplored high-pressure phase, which may be metallic, are also indicated on the figure.](http://what-when-how.com/wp-content/uploads/2011/03/tmp124118_thumb_thumb.jpg)
![Schematic diagrams exhibiting (a) a 3-D graphite lattice (b) a turbostratic structure,[24] and (c) a schematic structural model of the outer two layers for a multiwall carbon nanotube.[33] The inset in (a) depicts the A and B carbon sites denoted by open circles and the A' and B' sites by black circles. The in-plane lattice constant is denoted by a0, and the vectors of the unit cell in the direction a1, a2, and c are indicated. The nearest-neighbor carbon distance aC_C in graphite is 1.421 A. Schematic diagrams exhibiting (a) a 3-D graphite lattice (b) a turbostratic structure,[24] and (c) a schematic structural model of the outer two layers for a multiwall carbon nanotube.[33] The inset in (a) depicts the A and B carbon sites denoted by open circles and the A' and B' sites by black circles. The in-plane lattice constant is denoted by a0, and the vectors of the unit cell in the direction a1, a2, and c are indicated. The nearest-neighbor carbon distance aC_C in graphite is 1.421 A.](http://what-when-how.com/wp-content/uploads/2011/03/tmp124119_thumb_thumb.jpg)
![Comparative study of transverse magnetoresistance at low temperature (as indicated in parenthesis) for highly oriented pyrolytic graphite (the dot-dashed curve),[34] typical mesophase-pitch-based carbon fibers heat treated at different temperatures (the solid curves),[13] vapor-grown carbon fibers (the dashed curve),[35] and multiwall carbon nanotubes (the dotted curve).[36] Vapor-grown carbon fibers exhibit a similar magnetoresistance behavior to that of multiwall carbon nanotubes. Comparative study of transverse magnetoresistance at low temperature (as indicated in parenthesis) for highly oriented pyrolytic graphite (the dot-dashed curve),[34] typical mesophase-pitch-based carbon fibers heat treated at different temperatures (the solid curves),[13] vapor-grown carbon fibers (the dashed curve),[35] and multiwall carbon nanotubes (the dotted curve).[36] Vapor-grown carbon fibers exhibit a similar magnetoresistance behavior to that of multiwall carbon nanotubes.](http://what-when-how.com/wp-content/uploads/2011/03/tmp124121_thumb_thumb.jpg)
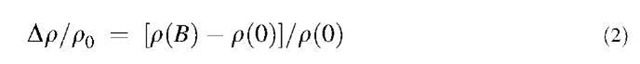
![Three typical structural models for SWNTs, where the nanotubes are related to rolling a graphene sheet into a cylinder.[2'3] Fullerene caps for the armchair and zigzag tubes are also indicated. Three typical structural models for SWNTs, where the nanotubes are related to rolling a graphene sheet into a cylinder.[2'3] Fullerene caps for the armchair and zigzag tubes are also indicated.](http://what-when-how.com/wp-content/uploads/2011/03/tmp124125_thumb_thumb.jpg)
![Model for graphite whiskers grown by the DC arc-discharge of graphite electrodes.[42] Whiskers were reported to have the carpet-rolling structure of graphite sheets and to have high mechanical strength and modulus along the fiber axis, similar to the ideal values of a graphene sheet. Model for graphite whiskers grown by the DC arc-discharge of graphite electrodes.[42] Whiskers were reported to have the carpet-rolling structure of graphite sheets and to have high mechanical strength and modulus along the fiber axis, similar to the ideal values of a graphene sheet.](http://what-when-how.com/wp-content/uploads/2011/03/tmp124126_thumb_thumb.jpg)
