INTRODUCTION
Many important physical properties of natural or man-made aerosol particles such as light scattering, electrostatic charges, and toxicity, as well as their behavior involving physical processes such as diffusion, condensation, and thermophoresis, depend strongly on their size distribution. An important aerosol behavior mechanism affecting the size distribution of aerosol particles is coagulation. Aerosol particles suspended in a fluid may come into contact because of their Brownian motion, or as a result of their relative motion produced by external forces (e.g., gravity, hydrodynamic forces, electrical forces, etc.). The result is a continuous decrease in number concentration and an increase in particle size. The theory of coagulation was originally devised for particles in liquids and was later extended to aerosols. In the case of solid particles, the process is sometimes called agglomeration, and the resulting particle clusters are known as agglomerates. Therefore in many basic and applied fields (e.g., synthesis of nanostructured material via gas-phase synthesis), the evolution of the particle size distribution because of coagulation is of fundamental importance and interest.
Aerosol coagulation is caused by relative motion among particles. When the relative motion is because of Brownian motion, the process is called Brownian coagulation. Brownian coagulation is a spontaneous and ever-present phenomenon for aerosols. When the relative motion arises from external forces such as gravity or electrical forces, or from aerodynamic effects, the process is called kinematic coagulation. Kinematic coagulation includes gravitational coagulation, turbulent coagulation, electrostatic coagulation, etc.
The objective of this chapter is to review the theories of coagulation describing how particle number concentration and particle size change as a function of time. To do that, first, an overview of some important coagulation mechanisms is presented. Next, various solution techniques for the coagulation equation are comparatively reviewed.
COAGULATION OF MONODISPERSE AEROSOLS
When an aerosol contains particles of the same size, it is called monodisperse, whereas if particles are present in a variety of sizes, the aerosol is polydisperse. Coagulation of a monodisperse aerosol was developed for Brownian coagulation by Smoluchowski.[1] Smoluchowski derived the monodisperse coagulation equation by solving the diffusion equation around a single particle, and by obtaining the flux of other particles toward it. He assumed that particles adhere at every collision and that particle size changes slowly. The change in particle number concentration is represented by the following equation:
where N is the number concentration of the particles, t is the time, Kco (=2ndpD) is the Brownian coagulation coefficient in the continuum regime, dp is the diameter of the particles, and D is the diffusion coefficient of the particles. The diffusion coefficient D is given by the following Stokes-Einstein equation:
where kB is the Boltzmann constant, T is the absolute temperature, and m is the gas viscosity. Using Eq. 2, Kco in Eq. 1 can be expressed as follows:
By integrating Eq. 1, the number concentration is determined as a function of time as follows:
where No is the initial value for N.
Fig. 1 Coagulation of monodisperse aerosol particles.
Because the rate of coagulation is proportional to N2, it is rapid at high concentrations but decreases as coagulation reduces the concentration of particles. This relationship is shown in Fig. 1, which presents a plot of the number concentration of a monodisperse aerosol as a function of time. When the data are replotted as 1/N vs. t, a straight line is obtained. The quantity 1/N is in units of cubic centimeters and represents the average gas volume per particle. The slope of the line is the coagulation coefficient Kco.
GENERAL COAGULATION EQUATION
In ”Coagulation of Monodisperse Aerosols,” the equations describing coagulation were introduced for a monodisperse aerosol. We now consider the more complicated situation of polydisperse aerosols where a range of particle sizes is present. Because the rate of coagulation depends on the range of sizes present, the mathematics become much more complicated and no explicit solution exists.
The change in the particle size distribution of a poly-disperse aerosol by coagulation is represented by the following population balance equation:
where n(v,t) is the particle size distribution function at time t, and b(v,v) is the collision kernel for two particles of volume v and v. The first term in the right-hand side of Eq. 5 represents the increase in particles with volumes between v and (v+dv) from the combination of particles of volume v — v and v. The second term in the right-hand side of this equation represents the loss of particles with volumes between v and (v+dv) resulting from the coagulation of particles of volume v and v. Thus this equation gives an expression for the net rate of change of particles whose volumes lie between v and (v+dv). The collision kernel b(v,v) is dependent on the collision mechanism as well as on the particle size of two colliding particles.
COLLISION KERNELS
Brownian Coagulation
The Brownian collision kernel can be derived by either the kinetic theory of gases, or by the continuum diffusion theory according to particle size. Particles much smaller than the mean free path length of the gas molecules behave like molecules, and the kinetic theory of gases must be used to derive the collision kernel. In the meanwhile, for the particles much larger than the mean free path of the gas molecules, the continuum diffusion theory should be used. Generally, the Knudsen number Kn (=1/r), with l as the mean free path length of the surrounding gas molecules and r as the particle radius, is used to define the particle size regime.
In the free molecule regime, where the Knudsen number is larger than about 50, bfm(v,v) results from the kinetic theory of gases and is given as:[3]
lation coefficient for the free molecule regime and p is the particle density.
In the continuum regime, where the Knudsen number is smaller than about 1, bco(v,v) is derived by the continuum diffusion theory as follows:
where C = 1+Kn{1.142+0.558 exp(-0.999/Kn)} is the gas slip correction factor.[4]
The entire transition regime is characterized by Knudsen numbers in the range of ~ 1<Kn < ~ 50. In the transition regime, the coagulation rate is described neither by the continuum diffusion theory nor by the simple kinetic theory. Fuchs[5] found a semiempirical solution of the collision kernel by assuming that outside of a certain distance, namely, an average mean free path of an aerosol particle, the transport of particles is described by the continuum diffusion theory including the slip correction, and that inside the distance, the particles behave like in a vacuum and the transport is described by the kinetic theory. The two theories were brought together by matching the fluxes at the absorbing sphere radius.
This so-called flux matching was the basis for most of the following theories because of its phenomenological approach and the guarantee that the collision kernel is valid over the entire size regime. All theories dealing with an absorbing sphere use a correction function first calculated by Fuchs. This function is mainly expressed as an enhancement of the collision kernel for the continuum regime including the slip correction:
where KnD = and the subscripts ”co” and ”fm” designate the continuum regime including the slip correction and the free molecule regime, respectively. Dahneke[6] described the diffusion process as a mean free path phenomenon. To obtain the coagulation coefficient, Dahneke also matched the two fluxes but at a distance which is the mean free path of the particles. To compare the different theories, the following general enhancement function f(KnD) is used:
Table 1 Coefficients for enhancement function f (KnD)
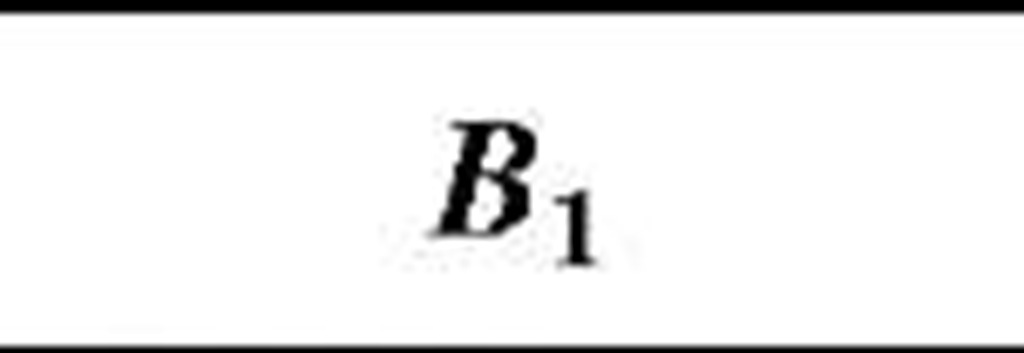 |
B2 |
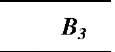 |
|
|
Fuchs[5] |
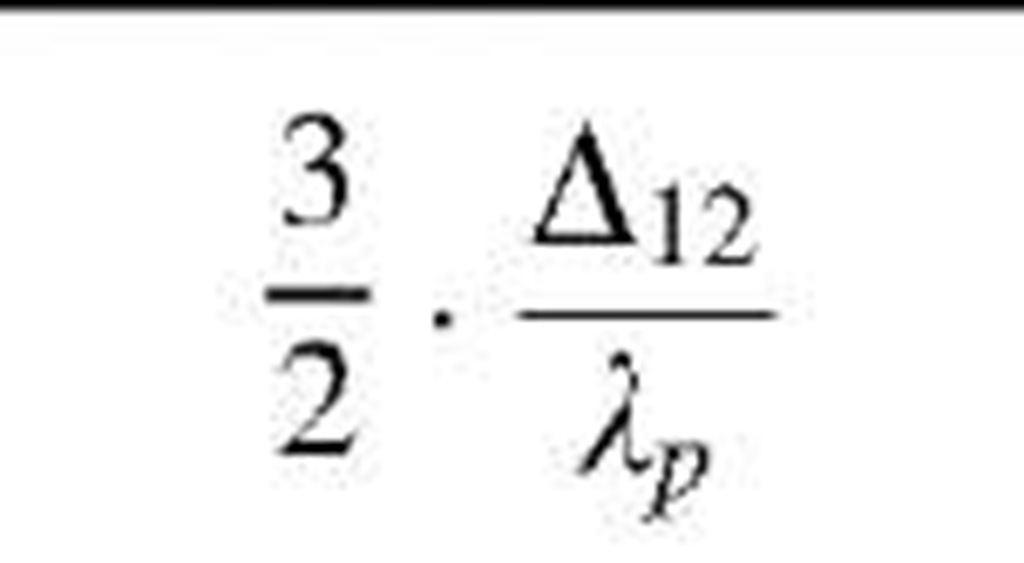 |
2 |
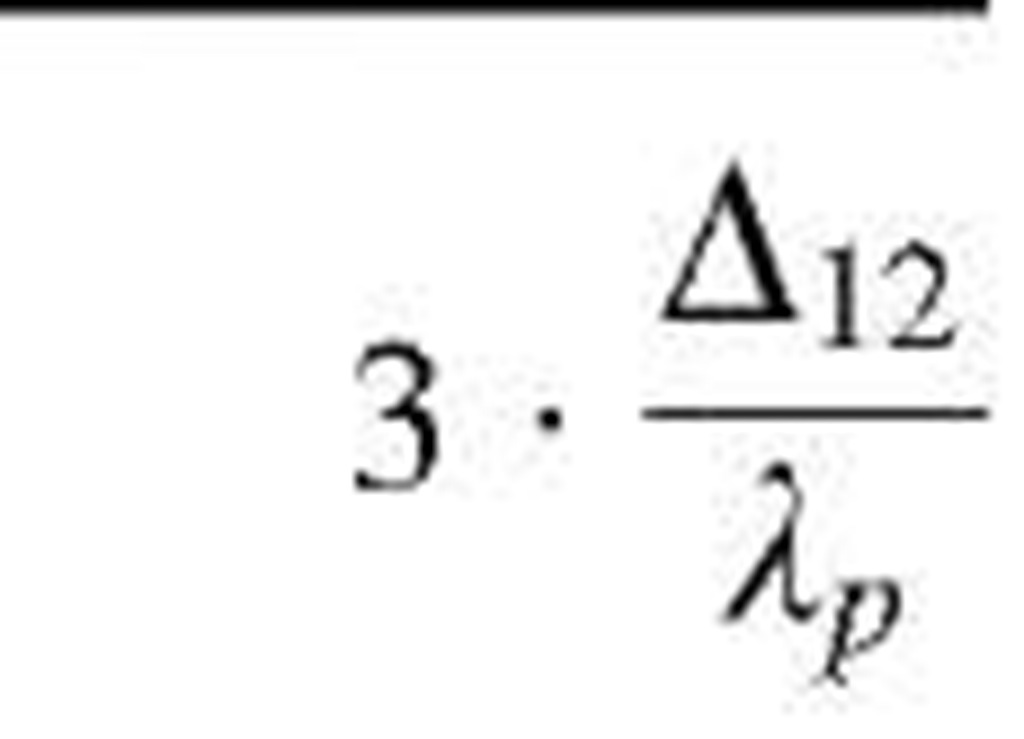 |
|
Fuchs and Sutugin[7] |
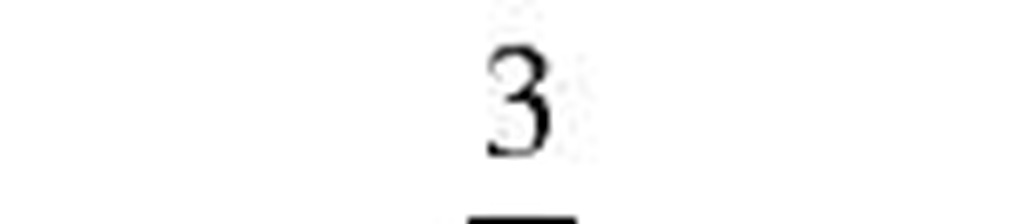 |
2.566 |
|
 |
|||
|
Dahneke[6] |
2 |
||
|
Harmonic mean |
2 |
The coefficients Bj, B2, and B3 are given for some theories in Table 1. By comparing various theories on the collision kernel in the transition regime, Otto et al.[8] recommended Dahneke’s theory to be used partially for its simplicity and partially for its accuracy.
Gravitational Coagulation
Kinematic coagulation is coagulation that occurs as a result of relative particle motion caused by mechanisms other than Brownian motion. From this section through ”Electrostatic Coagulation,” various kinematic coagulations are introduced.
Particles of different sizes will settle at different rates under the influence of gravity and thereby create relative motion between them, which leads to collision and coagulation. This mechanism is called gravitational coagulation. The collision kernel by gravitational coagulation is expressed as the following equation when the slip correction factor is neglected:[9]
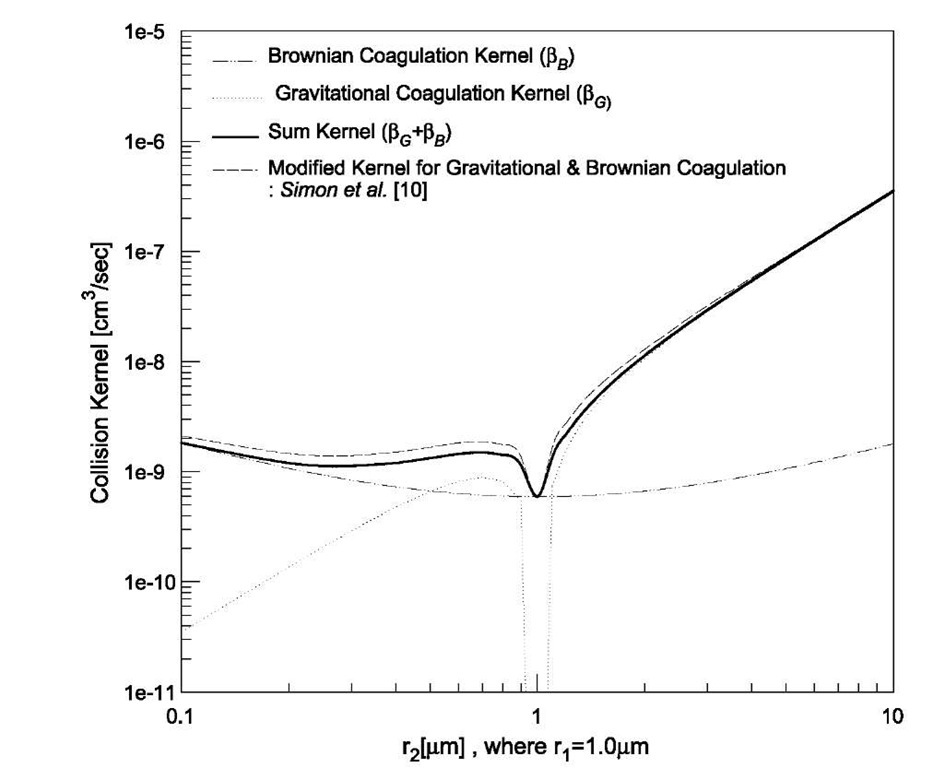
When both the Brownian and gravitational coagulations are significant, the two collision kernels bB and bG are commonly added to predict the behavior of aerosols. This simple addition would appear to be based on a physical picture of each of the mechanisms acting independently with neither affecting the other, but it would seem that this is not the case. Thus the combined kernel was suggested by Simon et al.,[10] and their kernel is plotted in Fig. 2 with the sum kernel and each kernel of the Brownian and gravitational coagulations. Their kernel describing the combined effect of Brownian and gravitational coagulations increases the rate of coagulation compared with the sum kernel in the size range of 0.1-1 mm. On the contrary, Qiao et al.[12] reported that weak Brownian diffusion, the effect of which is nonlinearly coupled with gravity, can act to decrease the coagulation rate.
Fig. 2 Comparison of Brownian and gravitational coagulation kernels.
Turbulent Coagulation
In many physical situations, the flow field in a fluid is turbulent. There are two ways in which turbulence causes collisions between neighboring particles. First, there are spatial variations of the turbulent motion. Because of this process, collision mechanism is conventionally called ”shear mechanism.” Second, each particle moves relative to the air surrounding it, owing to the fact that the inertia of a particle is different from that of an equal volume of air. Because the inertia of a particle depends on its size, neighboring particles of unequal size will have different velocities and this will also lead to collisions. This mechanism is called ”accelerative mechanism.” Saffman and Turner[13] derived the following collision kernel by combining the shear mechanism and the acce-lerative mechanism:
where r; [=(3v;74p)1/3] is the particle radius, pf is the fluid density, pp is the particle density, e is the turbulent energy dissipation rate, and v is the kinematic viscosity of the fluid. The particle relaxation time t including the Cunningham slip correction factor Cc,; is defined as:
where m is the dynamic viscosity of the fluid. The average acceleration of eddies in the dissipation range
The first and second terms in the square root term on the right-hand side of Eq. 12a represent the accelerative mechanism and shear mechanism, respectively. However, under more vigorous turbulence or with larger particles, the approaching particles may no longer be entrained completely by the smallest eddies, so they will have less correlated velocities.
Recently, Kruis and Kusters[15] analyzed this problem using a turbulence spectrum, which describes both the viscous subrange and the inertial subrange. In their work, the relative particle velocity w is represented by the following equations:
The root mean square (rms) fluid velocity vf is expressed as:
where g is the spectrum constant, which usually has a value between 10 and 100. The turbulent energy k (k =3/ 2vf2) and the dissipation rate e are obtained mostly from fluid dynamic simulations. The added mass coefficient b is defined as:
The dimensionless particle relaxation time 0, is defined as:
where TL is the Lagrangian time scale:
The rms particle velocity v,, valid in both the viscous and the inertial subranges of turbulence, is represented as:
whereas the velocity correlation is (see equation below): Electrostatic Coagulation
Charged particles may experience either enhanced or retarded coagulation rates depending on their charges. For a unipolar aerosol, it is necessary to consider electrostatic dispersion (i.e., the tendency of charged particles of the same sign to move away from each other). This dispersion tends to reduce the concentration of an aerosol, for example, by causing particles to deposit on the walls of any containing vessel or nearby surface. In the presence of particle charging, the collision kernel of particles must be corrected by:
where the subscript ”n” designates neutral particles. The Fuchs stability function W is given by:[16]
where zj and z2 are the numbers of unit charges contained in particles, and e is the electron charge. For k >0 (like charge), W>1 and coagulation is retarded from that for neutral particles. Conversely, for k<0 (unlike charge), W< 1 and coagulation is enhanced.





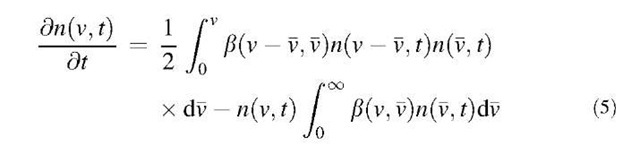
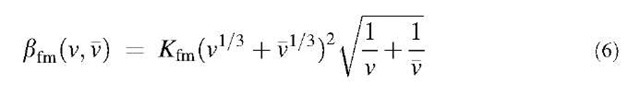
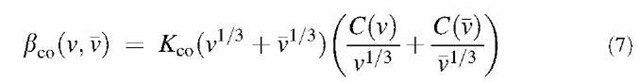

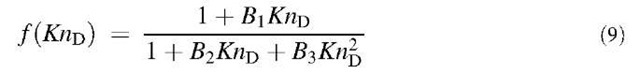

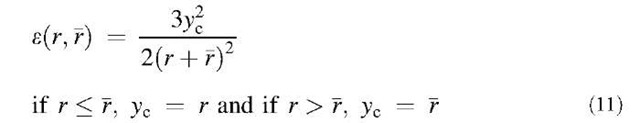
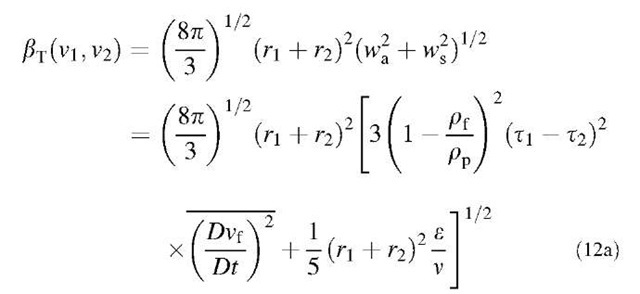







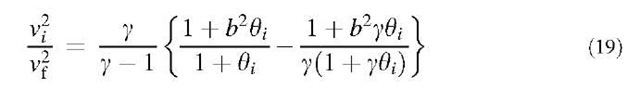

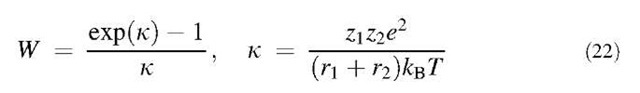
![tmpD5-90_thumb[1] tmpD5-90_thumb[1]](http://what-when-how.com/wp-content/uploads/2011/03/tmpD590_thumb1_thumb.jpg)
