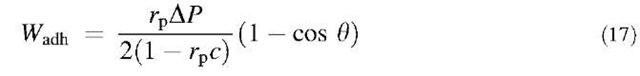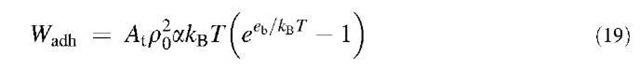EXPERIMENTAL VERIFICATION OF THE MODEL
To test this model, a suitable technique is based on vesicle adhesion measurement by micromanipulation.1-6-1 It consists in holding a slightly deflated 10- to 30-p.m vesicle in a micropipette with a controlled aspiration. At the start of the experiment, the shape of the vesicle is a segment of sphere outside of the pipette and a cylindrical portion inside the pipette (which ends in an hemisphere of radius equal to the inner radius of the pipette, rp). The knowledge of the initial diameter of the vesicle, the length of cylindrical part, and the pipette inner diameter allows one to determine the surface and volume of the vesicle. Facing the vesicle is the substrate with a known geometry. For instance, in Fig. 3 is shown the case of a vesicle facing a bead. The vesicle is then moved and placed in tangential contact with the substrate. If adhesion occurs, e.g., through weak ligand-receptor bonds, the vesicle will stretch following the shape of the substrate in order to increase the contact area. The volume and surface of the vesicle remain essentially constant throughout the whole process. Therefore, adhesion requires the volume and surface of the vesicle outside the pipette to be larger than it originally was. This is achieved by a decrease of the projected length inside the pipette. The adhesion energy can then be deduced through the Young-Dupre equation:
Fig. 3 Micromanipulated vesicle in contact with a bead held by a micropipette. The bar represents 5 mm. The measurement of the contact angle 0 directly gives the adhesion energy through the Young-Dupre equation (Eq. 15).
where 0 is the contact angle, Wadh is the adhesion energy as defined above, and g is the tension of the vesicle, which is obtained by applying the Laplace equation to the outer part of the vesicle and to the hemisphere at the tip of the cylinder inside the pipette:
Here c is the average curvature of the vesicle and DP is the aspiration (i.e., the difference in pressure between the outside and inside of the pipette). Combining Eqs. 15 and 16 gives:
It is possible to obtain an accurate value of Wadh by plotting DP as a function of G:
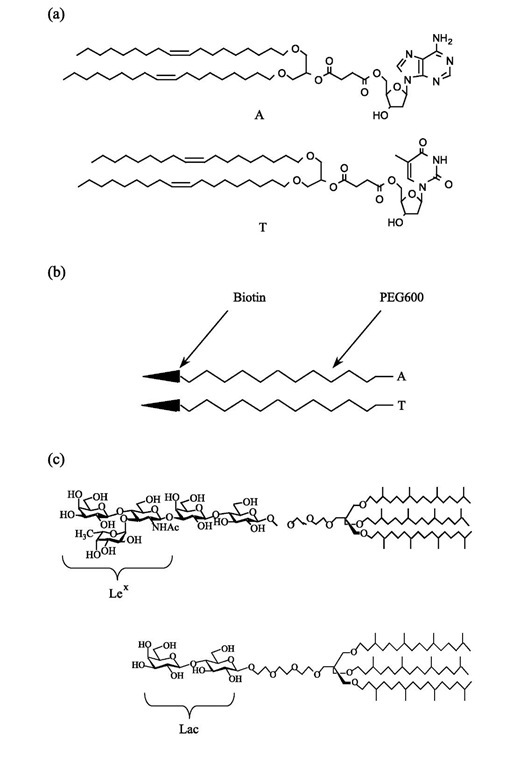
The slope of the graph is then exactly Wadh. To make sure the adhesion process is reversible, it is necessary to make cycles of decreasing-increasing aspiration pressure. It will not work in the case of strong bonds with lifetimes longer than the experimental characteristic time: the membrane is then pinned on the substrate and the receding contact angle will be larger than the advancing one. Therefore, to test the model, it is necessary to use weak bonds with well-known binding energies. Nucleo-sides such as adenosine and thymidine are good examples of such bonds.[7,8] For this purpose, lipids carrying one nucleoside (adenosine, A, or thymidine, T) as a polar headgroup were synthesized (Fig. 4a). Giant vesicles were formed by hydrating a lipid mixture of stearoyl-oleoyl-phosphatidylcholine (SOPC)/nucleoside lipid (9/1) (after evaporation from chloroform solution) in 320 mOsm sucrose solution.[9] The vesicle suspension was added to an aqueous glucose solution chamber of a slightly higher osmolarity (360 mOsm) than that of the vesicle in order to deflate it and make it micromanipulable.
The substrates were superavidin-coated polystyrene beads purchased from Bangs Labs. The average area per attachment site for biotin was of a few hundreds of nanometers squared per effective binding site. To coat them with nucleosides, a polyethylene glycol (PEG) spacer arm was dissymetrically functionalized at one end with biotin, and at the other end with a nucleoside (A or T) (Fig. 4b). The beads were incubated in water (50 mg/ ml) with one of these heterobifunctionalized PEG arms (1 mg/mL) for 1 day. The contact angle was measured for several tension values of the flaccid vesicle membrane by decreasing the aspiration and then increasing it to check for the reversibility of the adhesion. This decreasing/ increasing aspiration process was repeated several times on the same vesicle/bead couple, and, as expected, it was observed that this adhesion was reversible within the experimental error.
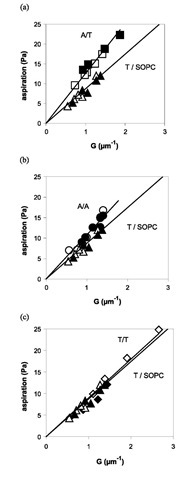
Four adhesion situations were investigated: A bead-A vesicle, T bead-T vesicle, T bead-A vesicle, and A bead-T vesicle. A control experiment was performed in which the vesicle was made of only SOPC and adhered to a T-coated bead. It turns out that the adhesion measured in the control experiment cannot be neglected, meaning that there is a nonspecific adhesion that has to be subtracted from the measurements to obtain the actual value of Wadh due to the bonds. Fig. 5 shows the aspiration pressure as a function of G for the different cases. The resulting values for Wadh, reported in Table 1, are independent of the vesicle size.
Given the experimental error, the A bead-T vesicle and T bead-A vesicle systems have the same adhesion energy, as expected. It may be observed that the specific adhesion energies follow the increasing order: Wadh(T/T)< Wadh (A/A)< Wadh(A/T). This is consistent with the data reported in the literature.[7,8] The short lifetime of the bonds is illustrated by the small fraction of occupied bead sites (5%) that can be estimated from the specific adhesion energy, the known bond energy, and the bead site density.
By using Eq. 13 one directly obtains eb from the measured specific adhesion energy values if poa is known. As the same grafting technique was used for the A and T beads, poa should also be the same in all the cases and is expected to be of the order of 10—4. We can therefore try to find a value that conciliates the four types of adhesion data (A/T, T/A, A/A, T/T). poa=2.4 x 10—4 gives values that are in closest agreement with the known binding energy values.[7,8] This value for poa seems reasonable because the a should be of the order of a fraction of the polar head of the lipid (a few tenths of nanometers squared) and of the po order of 1015 molecules/nm2. The accuracy on poa can be estimated from Table 2 where the binding energy values assuming different values of poa near the best one are given.
Fig. 5 Aspiration pressure as a function of G (cf. Eq. 18) for a specific interaction and comparison with the nonspecific case T/ SOPC (control). According to Eq. 3, the slopes are equal to Wadh. The solid lines are fits forced through zero and they roughly represent the adhesion energy. However, the values reported in Table 1 are averages from fits not forced through zero and in which the increasing pressure is treated separately from the decreasing one. Closed (open) symbols correspond to the increase (decrease) of the aspiration pressure. (a) A bead-T vesicle, (b) A bead-A vesicle, (c) T bead-T vesicle.
Experimentally, the equilibrium seems to be reached in less than a minute for each change of aspiration pressure. This result may seem surprising because it generally takes about 15 min for lipids to diffuse around a giant vesicle. Given Wadh and Eq. 10, the enrichment is around 1% at the true equilibrium obtained within 15 min. This negligible amount is within the experimental error of Wspe. This was fully checked experimentally as the measured contact angle did not vary significantly for 20 min at a given aspiration pressure. In this approximation, equilibrium can be obtained locally because of the excess of sites on the vesicle, and lateral diffusion does not bring significant change. The local equilibrium time is typically the one needed for a lipid to explore an area 1/p0, which is less than a second. This explains the fast equilibrium and why the observed hysteresis is not stronger than for nonfunc-tionalized vesicles.[10] In contrast, if there were more sites on the bead or less sites on the vesicle, the diffusion of the vesicle sites toward the contact region would noticeably change the equilibrium time.
Therefore, the description relating adhesion energy measurements to binding energies through Eq. 13 is satisfactory and can be applied to other systems. The main limitation is the requirement to know poa because it is not easy to obtain, but numerical simulations may provide good estimates in some cases. The vesicle micromanipulation technique is also a good approach to measure binding energies in this way. The precision of the technique is given by the dispersion of the adhesion energy data. In the case of weak bonds like A/T where this dispersion is seen in Table 2, the error is about 0.5kBT.
Table 1 Adhesion energy values (W) averaged, as indicated in Fig. 5, from at least two separate experiments and six cycles
|
A bead-T |
T bead-A |
A bead-A |
T bead-T |
T bead-SOPC |
|
|
|
vesicle |
vesicle |
vesicle |
vesicle |
vesicle |
|
W (mJ/m2) |
12.0 |
12.9 |
9.9 |
9.3 |
8.6 |
|
Wadh (mJ/m2) |
3.4 |
4.3 |
1.3 |
0.7 |
A BIOLOGICALLY RELEVANT APPLICATION OF THE APPROACH
Molecular features governing the selectivity in cell-cell recognition and adhesion are key elements to understand morphogenesis and organogenesis. All living organisms are characterized by the presence of glycoproteins and glycosphingolipids (GSLs) on the cytoplasmic membrane. Carbohydrate chains, being exposed structures at the cell surface, should play an essential role in early events of cell-cell recognition. Indeed, they have firmly been recognized as interaction sites in cell adhesion processes such as leukocyte recruitment or host-pathogen interaction. Such events are commonly attributed to lectin or lectinlike proteins and the corresponding specific carbohydrate ligands. It has been suggested only a decade ago that specific carbohydrate-carbohydrate interactions may also play this important role.[11] Several direct measurements of adhesion between surfaces decorated with glycolipids have been reported in the past.[12-18] These strong adhesions, obtained through various techniques (surface force apparatus, osmotic stress method, and vesicle micromanipulation), were due to van der Waals or other nonspecific forces. However, some carbohydrate-carbohydrate interactions found in biological processes, have been proposed to be specific.[11,19,20] One of them, the Lewisx determinant (Lex) has been identified as pre-sumably playing a biological role by means of intermem-brane interactions. According to current hypothesis, it has a calcium-mediated specific interaction with itself.
Table 2 Binding energy values (eb) as deduced from Eq. 17 for different values of r0a
|
|
|
|
Literature |
|
|
P0 a |
1.9 x 10—4 |
2.4 x 10—4 |
3.1 x 10—4 |
values |
|
A/T |
2.9 |
3.2 |
3.4 |
3.6 |
|
T/A |
3.1 |
3.4 |
3.6 |
3.6 |
|
A/A |
2.0 |
2.3 |
2.5 |
1.9 |
|
T/T |
1.5 |
1.7 |
1.9 |
1.5 |
Lex has been shown to be involved in murine and human embryogenesis. This carbohydrate is present on the cell membrane in the polar headgroup of glycolipids. It is not expressed at the cell surface until the eight-cell stage, shows maximal expression at the morula stage of mouse embryogenesis, and declines after compaction.[21,22] This compaction stage could be inhibited either by anti-Lex antibodies, Lex itself, or by inactivating the calcium with Ethylenediaminetetraacetic Acid (EDTA). As Lex is not charged, the role of the calcium is not of an electrostatic nature. These results[23,24] led the authors to propose a calcium-mediated Lex-Lex specific homotypic interaction as a basis of cell adhesion in preimplantation embryos and in various tumour cells. Other observations also strongly suggest that Lex-Lex interactions exist in the presence of Ca2+.[25-28]
The approach described above made it possible to conduct the first direct quantitative measurements of this putative interaction in a physicochemically well-defined system and in conditions similar to the natural environment of the glycolipid, i.e., lipid bilayers. This was done through the adhesion between two giant vesicles functio-nalized with synthetic glycolipids.
The Lex determinant is a trisaccharide, which, in classical natural sphingolipids, is attached to the ceram-ide through a lactose group. For this study, a lipid[29] with a Lex headgroup attached to hydrophobic chains via a ”spacer” group to ensure its mobility was synthesized (Fig. 4c). In this synthetic glycolipid, a rather low solubility in water together with good bilayer cohesion was obtained by using three hydrophobic chains instead of two as in ceramide. To ensure good accessibility of the Lex groups for interaction, they were provided with trans-lational mobility by branching the chains. This hinders the bidimensional crystallization of the chains and keeps the layers in a fluid state. Orientational mobility was provided by a flexible spacer between the chains and the Lex. This allowed the Lex groups to take the exact orientation and position for which the specific interaction can occur.
For the controls, a glycolipid with the same features but without Lex was synthesized (Fig. 4c) that will be referred to as Lac lipid.
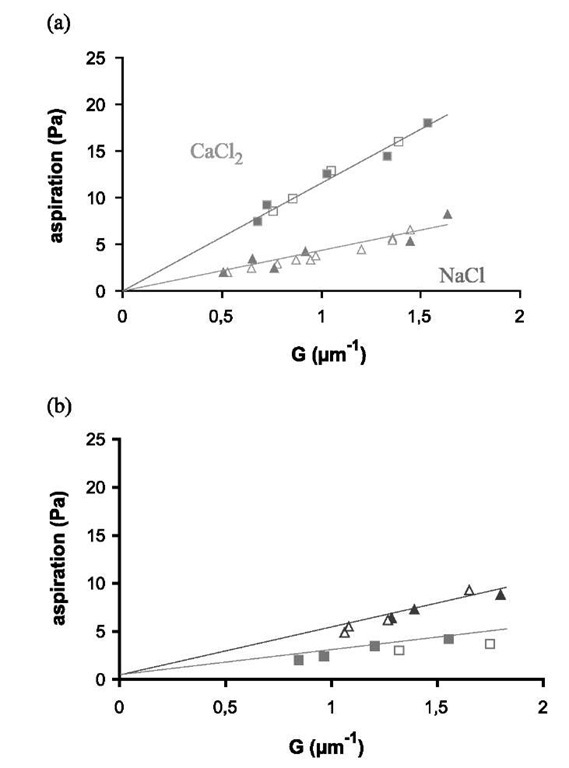
Fig. 6 Aspiration pressure as a function of parameter G given in Eq. 18: (a) Lex/Lex experiment (two vesicles with SOPC/Lex, 90:10); (b) Lex/Lac experiment (one vesicle is SOPC/Lex, 90:10, and the other is SOPC/Lac, 90:10); The closed symbols represent decreasing aspiration, and open ones are for increasing aspiration. Triangles are for NaCl solution and squares for CaCl2. The straight lines are least square fits.
Giant vesicles were formed exactly in the same way as for the A and T vesicles by lipid hydration (after evaporation from chloroform solution) in 320 mOsm sucrose solution. The Lex-functionalized vesicles, hereinafter referred to as Lex vesicles, were made from a mixture of SOPC and the synthetic Lex lipid (90:10 mol ratio). Control vesicles were made of SOPC and Lac lipid (90:10 mol ratio) and will be called Lac vesicles.
Two vesicles were transferred into another chamber filled with salt solution (either NaCl or CaCl2 at 360 mOsm). As in the previous experiment, both vesicles were micromanipulated into tangential contact. One of the vesicles represents the substrate. It is strongly aspirated so that its spherical shape is not modified throughout the whole process. The contact angle was measured for several tension values of the other vesicle membrane by decreasing the aspiration and then increasing it to check the reversibility of the adhesion.
The experiments consisted in comparing the adhesion of two Lex vesicles in NaCl and in CaCl2 (Lex/Lex experiments). As calcium is sometimes known to produce peculiar effects on bilayer interactions,[30] it was necessary to compare Lex/Lex experiments with experiments in which the Lex groups from one of the vesicles were absent (Lex/Lac experiments).
Fig. 6 shows the aspiration pressure as a function of G (cf. Eq. 17) for the controls and Lex/Lex experiments. As before, the slopes are equal to the vesicle adhesion free energies and are independent of the vesicle size. Adhesion energy values for the controls and for the Lex/Lex experiments are given in Table 3. The effect of adding calcium on the Lex vesicles is clearly seen in Table 3 and in Fig. 6. The adhesion energy in CaCl2 is 2.5 times higher than in NaCl whereas the Lex/Lac experiments showed a small decrease of the adhesion energy with calcium (3 x 10— 6 J m ). These results unambiguously show that Lex groups are necessary on both vesicles for the calcium-induced adhesion enhancement to occur. This is in agreement with the specific interaction scheme advocated by Hakomori.[11]
The adhesion, in the case of NaCl and for both types of vesicles, is the result of a balance between van der Waals attractions and short-range repulsions that include entro-pic and structural contributions.1-15,31-1 Therefore, the higher adhesion in NaCl in the Lex/Lac system as compared to Lex/Lex may seem surprising. However, one may note that the sugar groups are bound to the lipid chains by a flexible spacer (Fig. 4c). The thermal fluctuations of this spacer can cause steric repulsions as polymer brushes do.[32] This difference between Lex/Lex and Lex/Lac experiments is not relevant for our purpose because van der Waals forces do not play a significant role in cell membrane interactions. Usually, the adhesions are governed by cell adhesion molecules such as proteins or lipids given that there are many steric repulsions produced by the glycocalix. For this reason, two biomembranes will not adhere in the absence of specific adhesion sites.
Table 3 Adhesion energy of vesicles (10— 6J/m2) in aqueous media between Lex- or Lac-functionalized vesicles in NaCl and in CaCl2
|
Left vesicle/right vesicle |
Adhesion energy (|iJ/m2) In 0.2 M NaCl In 0.11 M CaCl2 |
|
|
Lex/Lex Lex/Lac |
4.5±2 5.4±2 |
11 ±2 2.5±2 |
The specific contribution Wadh of the Lex groups to the adhesion energy of our vesicles is equal to the difference between the effects of calcium on adhesion energy in the Lex/Lex and in the Lex/Lac experiments. Table 3 shows that Wadh=10±5 mJ m— 2. This adhesion is weak for the density of sugar that was used. This indicates that the interactions must be weak and therefore that the lifetime of the bonds is small. Thus, the case of Lex is favorable for the use of the model of a cell adhering to a substrate. This is confirmed by the fact that a single slope for the contact formation and separation of the vesicles are identical, meaning that the adhesion is continuous and reversible. Eq. 9 gives an enrichment smaller than 2%. Therefore, the density can be considered as constant. This has the consequence that the density of sites on the substrate can be taken as the initial density of Lex in the vesicles, which is 1.4 x 1017 molecules/m2. In addition, ap0Ac will be much smaller than At. Therefore, Eq. 13 can be rewritten here:
Because the Lex are in the polar head of the lipids, a should be of the order of the polar head of the lipid. A good estimate seems to take the same value as that measured with two membranes made of A and T lipids:[33] 0.3 x 10—18 m2. With these values, eb ranges between 0.17 and 0.5kBT(i.e., 0.1 and 0.3 kcal/mol). Previous glycolipid studies showed strong van der Waals interactions.1-12-16,18-1 In the present work, the calcium-induced interaction is specific and comes in addition to van der Waals forces. Note that these molecules are neutral and therefore this interaction is not intrinsically electrostatic.
This ultraweak interaction energy validates the assumption that the binding energy is substantially below kBT. A rough estimate of the bond lifetime can be obtained by comparison with the streptavidin/biotin system (30kBT bond energy and lifetime of several days) and assuming an Arrhenius law. It is well below 1 msec. It is most unusual to measure molecular interaction energies well below the thermal energy. This only shows that cell-cell adhesion will require a large number of these molecules as is indeed observed during the morula stage of mouse embryogen-esis. The molecular mechanism of the Lex interaction still remains mysterious. The mediation by Ca2+ could result from the setting up of an appropriate coordination shell around the cation.[34]
These measurements with synthetically tailored Lex containing neoglycolipids could be analyzed with the model of a cell adhering to a substrate presented above. It directly confirms the involvement of neutral cell surface oligosaccharides in cell-cell adhesion and illustrates why, when the Lex sites are blocked, the compaction stage of the embryo does not occur.[23] Lex is capable, in the presence of Ca2+, to substantially enhance the deformation and adhesion of lipid vesicles, i.e., objects with mechanical features akin to those of the cell membranes. The interaction scaled down to one molecule is well below thermal energy. It produces transient and dynamic adhesion that is indeed what cell differentiation requires.
This direct measurement of biologically relevant carbohydrate/carbohydrate interaction shows that it is now possible to quantify such ultraweak bonds with the presented model. It opens up a new promising field in biology.
CONCLUSION
The simple model that describes cell adhesion on a substrate gives quantitatively good results and allows one to relate the adhesion energy to the excess of ligand in the contact zone and to the molecular binding energy. The experimental approach that is presented can be used to describe the properties of adhesion molecules that produce weak bonds. In contrast, for vesicles bearing stronger binding sites, Eq. 9 is not valid anymore. However, some information about the ligand receptor information can still be obtained.[35] The adhesion molecules are expected to diffuse toward the contact zone, which therefore should contain a higher density of adhesion molecules, leaving the noncontacting part of the vesicle depleted, especially for large contact areas.
Also, this model deals only with adhesion at equilibrium. With the same kind of approach, it is possible to try to understand the formation dynamics of the contact zone. More precisely, the nucleation of patches can appear during the spreading of the contact. This has been discussed elsewhere.[36]
Finally, the case of real biological cells is much more complicated to quantify, as there are many more parameters involved such as the glycocalyx, the cytoskeleton, and many adhesion molecules acting at the same time. The role of the glycocalix has been included in another approach by Bell et al.[4] The mechanical properties of a cell are very different from that of a vesicle and, although it has been tried in the past,[37,38] the measurement of the contact angle does not give very satisfactory results.