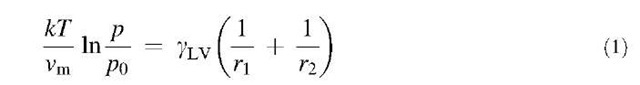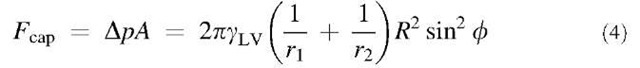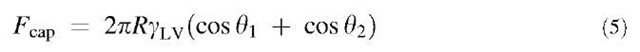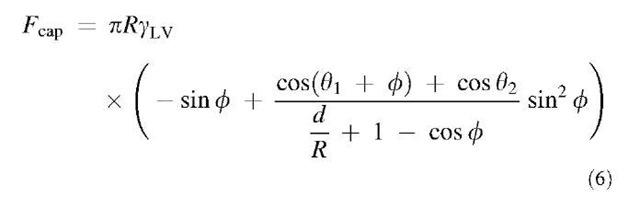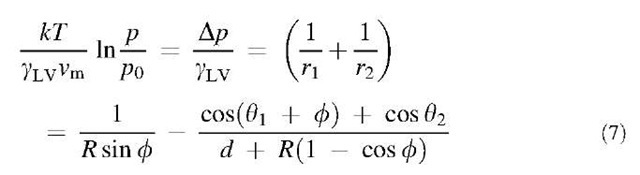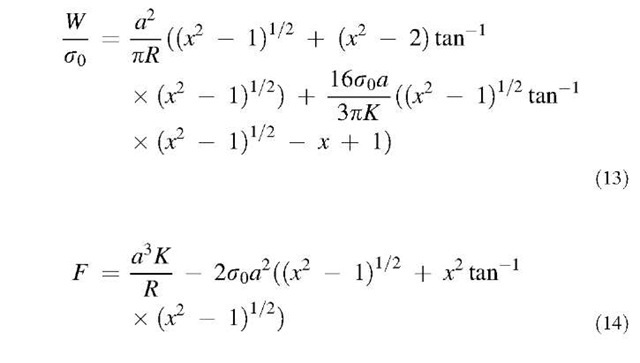INTRODUCTION
Self-assembled monolayers (SAMs) are monomolecular layers that are spontaneously formed on immersing a solid substrate into a solution containing active surfactant molecules. The best studied examples are silanes, which are used to modify, for example, silica and mica surfaces, and alkylthiols, which have an affinity for coinage metals.[1] Organic SAMs can be used to alter and control the chemical nature of surfaces. For instance, SAMs provide a robust base layer for immobilizing biological molecules in biosensors. The bonding of enzymes to alkanethiol SAMs on gold has received attention as a method of constructing enzyme electrodes.[2] Lee et al.[3] are developing a surface plasmon resonance-based mono-saccharide sensor by immobilizing a small thiol-based receptor molecule on gold containing a boronic acid group that is known to covalently bind the 1,2 or 1,3-diol of sugars. The success of SAM-based sensor applications depends on the stability of the underlying SAM as a function of aging and on environmental conditions such as humidity and temperature.
Self-assembly is simple and widely applicable in areas such as coatings, lubrication, templating, optoelectronics, and microelectromechanical systems/nanoelectromechan-ical systems (MEMS/NEMS). MEMS offers great promise for system integration of sensors, actuators, and signal processing. The miniaturization and integration offered by MEMS devices is attractive in applications where smaller size and weight are desirable. However, as devices become smaller, the surface area-to-volume ratio becomes larger and surface forces become more important. Factors determining the performance, reliability, and durability of MEMS devices are not well understood. In many applications, it will be impractical or impossible to protect MEMS devices from the operating environment. For instance, robust MEMS actuators must operate in a variety of conditions, some of which may be extreme (e.g., high temperature, a wide range of climatic conditions, and high vacuum).[4] In MEMS, nanoscale dimensions potentially separate device components where water can capillary condense, giving rise to stiction. Many applications for MEMS/NEMS are not really practical, as many studies have revealed the profound negative influence of stic-tion, friction, and wear on the efficiency, power output, and steady-state speed of microdynamic/nanodynamic devices.[5,6] Komvopoulos and Yan[7] have shown that liquid bridging at intermediate humidity is the dominating short-range attraction mechanism prevailing at MEMS interfaces. It is also known that head/disk stiction occurs at humidities greater than 80%.[8] The ubiquitous presence of water vapor makes the study of the effect of relative humidity (RH) on the performance and reliability of MEMS devices crucial. Depositing a hydrophobic SAM on a hydrophilic surface can reduce surface wettability. Organosilane SAMs are being investigated as boundary lubricants and antiwetting coatings in MEMS devices to reduce the effect of humidity on friction and wear.
In order for SAMs to be useful as boundary lubricants, in biosensors, as MEMS coatings, and in a variety of other applications, it is important to understand the effect of environmental conditions such as humidity and temperature on SAM robustness and stability. In this chapter, we present current research on the effect of humidity on the adhesiveness of alkyl-based SAM coatings on gold, silica, and mica. The wide variety of SAMs designed to be immersed in water (for instance functionalized SAMs for sensor applications) is not specifically discussed here, but this information should be pertinent for those interested in the effect of water on underlying SAM stability and adhesion.
CAPILLARY CONDENSATION AND ADHESION
In studies of physisorbed surfactant monolayers on mica, Chen and Israelachvili[9] found that adhesion increased with RH and was dependent on the hydrophilicity of headgroups and the phase state of hydrocarbon chains. Humidity has also been shown to increase the mobility of surfactant molecules on the surface by penetrating into the headgroup region and by weakening the attraction between the surfactant molecules and the mica.[10,11] Humidity affects adhesion between surfaces because when the surfaces are close enough, water capillary condenses around the contact zone as long as the sum of the water contact angles on the two surfaces is less than 180°.[12] This annulus gives rise to an attractive capillary force in addition to any direct solid-solid adhesion that must be overcome to separate the surfaces. The capillary pressure depends on the relative vapor pressure according to the Kelvin equation:
where r1 and r2 are the meniscus radii of curvature, k is the Boltzmann constant, T is the temperature, gLV is the liquid-vapor surface tension, p/p0 is the vapor pressure, and vm is the molar volume of the condensed liquid. It is assumed that the vapor is ideal, the liquid is incompressible, and the molar volume of the vapor is much larger than the molar volume of the liquid. More complicated expressions can be used to account for these assumptions.[13,14]
The adhesive force because of capillary condensation is simply:
where Dp is the pressure difference across a curved interface acting on an area A. The Young-Laplace equation relates the Laplace pressure to the surface tension and local meniscus curvature as follows:
Considering the general case of a rigid sphere of radius R interacting with a rigid, flat plate (no surface deformations because of adhesive forces), the capillary pressure is given by:
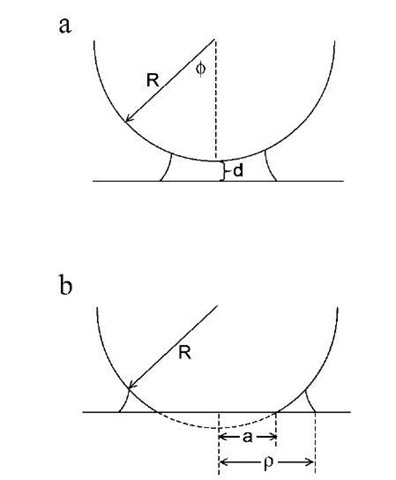
where f is the filling angle, as shown in Fig. 1a.[12] In the limit of vanishing filling angle, the capillary pressure is given by:
where d1 and d2 are the water contact angles on the two surfaces. If the filling angle is large, such as the tip of an atomic force microscope (AFM) in contact with a surface at high humidity, more complicated expressions are required, as detailed by Orr et al.[12] If the meniscus is assumed to be circular, the capillary force can be approximated as:[15]
Fig. 1 Schematic illustration of capillary condensation between a sphere of radius R and a flat plate. In panel (a), both the sphere and the flat are rigid. f is the filling angle and d is the sphere-plate separation. In panel (b), the sphere is deformable. a is the radius of the flattened contact zone and p is the distance from the contact center to the edge of the capillary condensate.
where the filling angle is fixed by the vapor pressure according to the Kelvin equation:
and d is the sphere-flat separation at the point of closest approach. In the case of an AFM tip, the resolved surface tension force may also be important and should be added. It is given as:
If the sphere and flat are elastic and adhesive, the theory of Johnson, Kendall, and Roberts (JKR)[16] is frequently used to explain surface deformation and adhesion in dry conditions. The JKR theory predicts a finite contact diameter even under zero load. The adhesive force is given by:
where W is the Dupre energy of adhesion given by:
where g1 and g2 are the surface energies of the contacting materials, and g12 is the interfacial energy between the two surfaces. If the materials are identical, then g12 = 0 and W = 2g. The JKR theory only takes into account the adhesive interactions inside the contact zone and neglects interactions between the surfaces outside the contact zone. Derjaguin, Muller, and Toporov (DMT)[17] approached the problem from a different point of view by treating the contact as Hertzian but taking into account the interactions outside the contact zone. Their theory predicts an adhesive force of:
Maugis[18] showed that these two theories are actually special cases of a theory derived using linear elastic fracture mechanics with an adhesive ”Dugdale” zone outside the contact area. In the Dugdale model, a constant adhesive stress is assumed to act between the surfaces in a region just outside the contact zone. Outside this region, the adhesive force falls to zero.
Maugis and Gauthier-Manuel[19] pointed out that capillary condensation is the perfect example of a Dugdale zone outside the contact area. The condensate occupies an annulus in which the adhesive stress is constant and is given by the Laplace pressure. Maugis took the stress outside the contact zone to be:
where a is the radius of the contact zone, p is the radius of the area covered by the condensate, and r is the radial coordinate (Fig. 1b). Maugis derived the following equations:
where x = p/a and F is the load on the system. Although it is not possible to simplify these equations further to obtain one equation that gives the load as a function of the contact radius, it is possible to solve these two equations using an iterative procedure. As shown in Maugis,[18] as p/p0! 0, JKR results are recovered and as p/p0! 1, DMT results are recovered.
The effect of humidity on the stability, wettability, and adhesion of SAM-coated surfaces depends on the ability of water to favorably interact with the monolayer. The contact angle of water on a SAM surface gives a good indication of SAM wettability. SAMs with hydrophilic terminal groups have low contact angles and adhesion is strongly affected by humidity because of capillary condensation. On highly hydrophobic SAMs, advancing contact angles are generally very high 110°) with receding angles slightly lower.[20] The hysteresis between advancing and receding angles provides a measure of the degree of surface roughness or heterogeneity.[1] Large contact angle hysteresis or contact angles that decrease with time indicate that water interacts somewhat favorably with the SAM. In the case of alkylsilane SAMs, it is likely that water changes the monolayer by penetrating to the SAM-substrate interface and by hydrolyzing the siloxane bonds. In these cases, humidity will affect adhesion near saturation.
ALKYLTHIOL SAMS ON GOLD
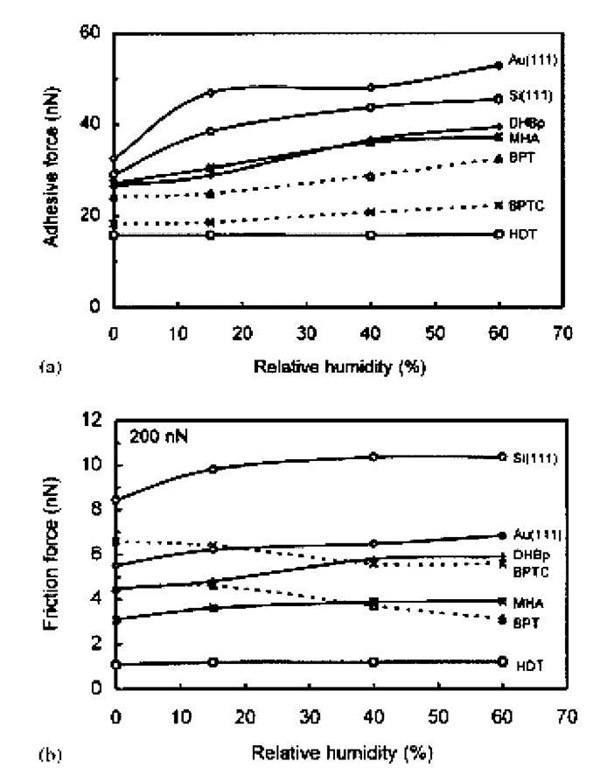
SAMs that are particularly effective in repelling water are alkanethiol SAMs deposited on gold. These SAMs are packed very tightly and are covalently bound to the gold substrate through the metal-sulfur bond. The alkyl chains of the thiols are in the all-trans conformation, tilted at an angle of ~ 20-30° from normal to the metal surface.[21] In general, these SAMs have very high advancing and receding contact angles, indicating that water is unable to disrupt the layer at least on the time scale of the experiment. Liu and Bhushan[5] used the AFM to measure adhesion between a silicon nitride tip and SAMs with different terminal groups deposited on Au(111) and Si(111) as a function of humidity up to 60% RH. Fig. 2 shows the adhesive force as a function of RH for bare gold and silicon, a carboxylic acid-terminated SAM (16-mercapto-hexadecanoic acid) on gold (MHA), a hydrox-yl-terminated biphenyl SAM (4,4′-dihydroxybiphenyl) on silicon (DHBp), a biphenyl SAM (1,1′-biphenyl-4-thiol) on gold (BPT), a cross-linked version of the biphenyl SAM (BPTC), and a hydrophobic SAM (hexadecane thiol) (HDT). Adhesion increases with RH for the uncoated and the hydrophilic SAM-coated surfaces. It increases less dramatically for phenyl-terminated SAM coatings and it is independent of humidity for the hydrophobic coating. This suggests that at least for humidities up to 60%, the methyl-terminated thiol SAM affords protection against capillary-induced adhesion.
Li et al.[22] found that the friction of a silicon nitride AFM tip on an alcohol-terminated SAM (C11OH) on gold is high at 10% RH but decreases with increasing humidity because water acts as a lubricant. Friction on a methyl-terminated SAM (C12) is independent of humidity even for immersion in pure water. However, as pointed out by Yoshizawa et al.,[23] there is no fundamental relationship between friction and adhesion even though they are sometimes highly correlated.
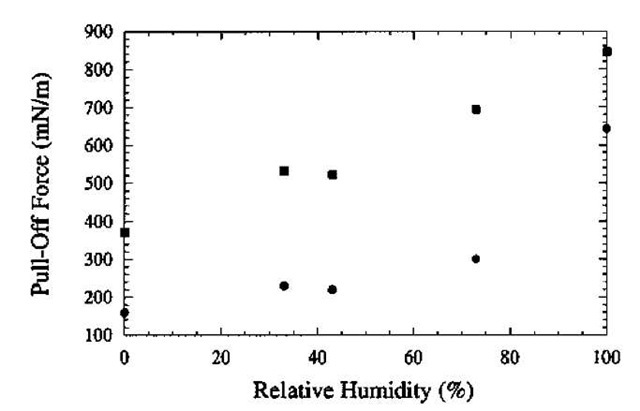
In contrast to AFM studies, Quon et al.[24] measured the effect of humidity on the adhesion between a SAM-coated gold surface [root mean square (rms) roughness 20 A] and a molecularly smooth mica surface using a surface forces apparatus (SFA).[25] In the SFA, the force is measured between cross-cylinders with radii of curvature
of approximately 2 cm. Because water wets mica (0 = 0), according to Eq. 5, it is expected that humidity will affect adhesion through capillary condensation. As shown in Fig. 3, for both alcohol- and methyl-terminated alkylthiol SAMs, adhesion increased with increasing RH. The magnitude of the adhesion at a particular RH was always higher for the alcohol-terminated SAM because the water contact angle is very small. Interestingly, near saturation, the adhesive force for the methyl-terminated SAM is much greater (643 mN/m) than is predicted by Eq. 5 (335 mN/m) if the SAM is assumed to be very hydrophobic (0^ 105°). The reason for this unexpectedly large adhesion is not clear. However, it suggests that water interacts with the hydrophobic surface to a greater extent than expected for an alkanethiol on gold.
Fig. 2 The influence of RH on the adhesive force between a silicon nitride AFM tip and Si(111), Au(111), and five SAMs: a carboxylic acid-terminated SAM (16-mercapto-hexadecanoic acid) on gold (MHA), a hydroxyl-terminated biphenyl SAM (4,4′-dihydroxybiphenyl) on silicon (DHBp), a biphenyl SAM (1,1′-biphenyl-4-thiol) on gold (BPT), a cross-linked 1,1′-biphenyl-4-thiol (BPTC), and a hydrophobic SAM (hexadecane thiol) (HDT).
Fig. 3 Pulloff forces (mN/m) as a function of RH. Separate SAMs were prepared for each data point: square symbols are for the alcohol-terminated SAM; circles are for the methyl-terminated SAM.