Linking Number Of DNA (Molecular Biology)

The linking number, Lk, is the defining property of DNA elementary topological domains. Generally speaking, Lk is a measure of the total number of complete revolutions that either strand makes about the other. As long as the strands remain intact, Lk is a fixed quantity. Two otherwise identical closed duplex DNAs (cdDNA) that differ only in Lk are termed topoisomers. Even though they contain exactly the same nucleotide sequence and covalent connections, the properties of the members of a family of topoisomers depend strongly on Lk. The linking number of DNA can be described formally in several different ways, all of which may be readily generalized to any two closed curves in space.

1. Properties of the Linking Number

The linking number has several simple and highly useful attributes. (1) Lk is an integer for superhelical DNA (but not necessarily for protein-sealed DNA loops)—this follows from the requirement that both strands be closed curves; (2) in general, Lk is constant as long as the topological domain remains intact—a topological domain may be broken by a single- or double-stranded DNA chain scission or, if appropriate, by the disruption of links to the protein sealing the domain; (3) the linking number is a topological quantity, and its value is independent of DNA geometry—that is, Lk does not vary with deformation of the trajectory of either strand or with changes in the characteristic duplex geometric quantities (pitch, roll, twist, tilt, propeller twist, etc); (4) the linking number is independent of the ordering of the two curves; thus, for two DNA strands this independence of ordering clearly distinguishes the linking number from the twist; and (5) finally, the double-helix structure of DNA defines a duplex axis (A) that is considered to be a continuous line along the center of the helix. Since either of the two backbone chains can be continuously deformed into the axis, the linking number of either strand about the axis is the same as the linking number of the strands about one another. Thus, for example,

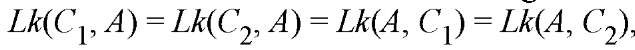and so on. The validity of these equalities requires, of course, that the duplex axis be everywhere defined. If it is not (eg, a cdDNA containing regions of local denaturation or of cruciform extrusion), a more extensive treatment might be required (1).

2. Formal Definition and Calculation of the Linking Number

2.1. The Index Approach

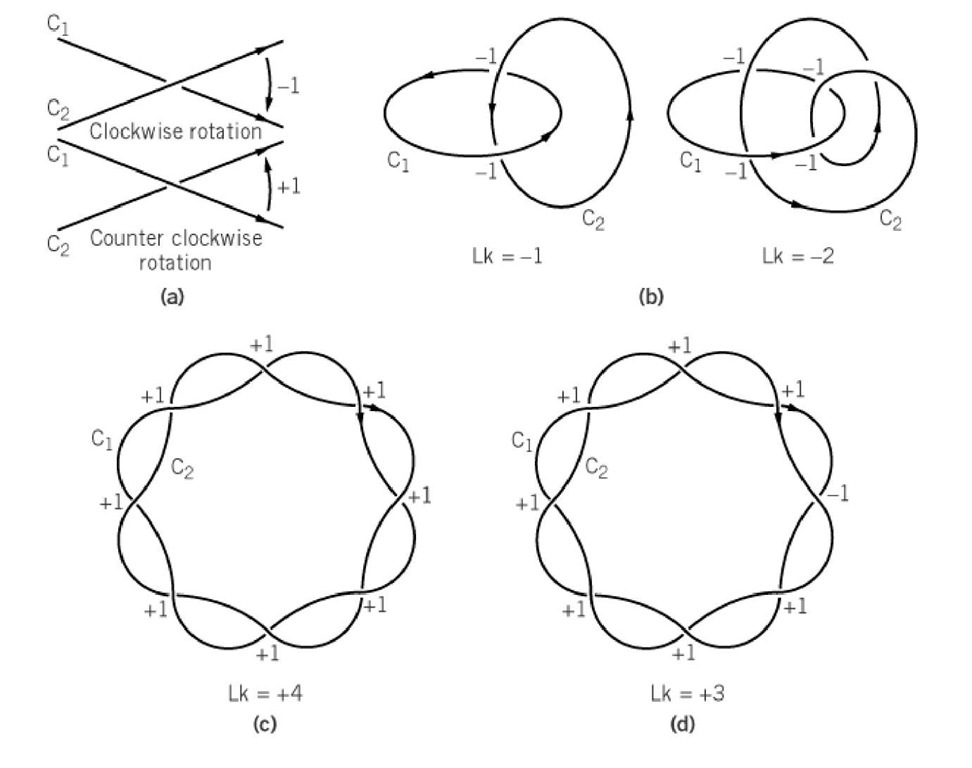
Conceptually, the easiest method of determining Lk is the index approach. This method relies on the criteria that the two strands must wind about each other once for each contribution to Lk, and that the sign of each local contribution depends on the relative orientation of the curves. A description of how to assign index numbers is presented in Figure 1. The linking number does not depend on the perspective of the observer, so the DNA may be viewed in projection onto any convenient plane. The strands are assigned parallel orientations, in order to be consistent with the conventions used in the mathematical literature.

Figure 1. Calculation of the linking number using the index approach. (a) Assignment of strand orientations and index numbers at projection crossings. The curves are oriented in a parallel sense. Clockwise rotation of the tangent of the upper curve to coincide with the tangent of the lower curve at the intersection point contributes -1; counterclockwise rotation of the tangent of the upper curve to coincide with the tangent of the lower curve at the intersection point contributes +1. (b) Two examples of the use of the index approach to calculate Lk. In each case Lk is one-half the sum of the index numbers. (c) Representation two oriented curves that intersect eight times in projection. Each index number is +1, giving Lk = +4. (d) Calculation of Lk for a case in which some of the intersections cancel. This structure, which appears similar to that of (c), has Lk = +3.

The easiest way to construct the backbone chain curves C1 and C2 is to draw a line along one strand with its arrow pointing 5′ ^ 3′, and along the complementary strand with its arrow pointing 3′ ^ 5′. (This parallel orientation should not be confused with the polarities of the strands, which are, of course, antiparallel.) According to this convention, each interstrand crossing in the projection is assigned an index value of+1 if the locally upper strand must be rotated counterclockwise so as to make its tangent vector coincide with that of the locally lower strand. An index value of -1 is assigned for the reverse case. Then Lk is one-half the sum of all these index values, since each local contribution to Lk requires two crossings to advance one turn.

2.2. The Surface Intersection Approach

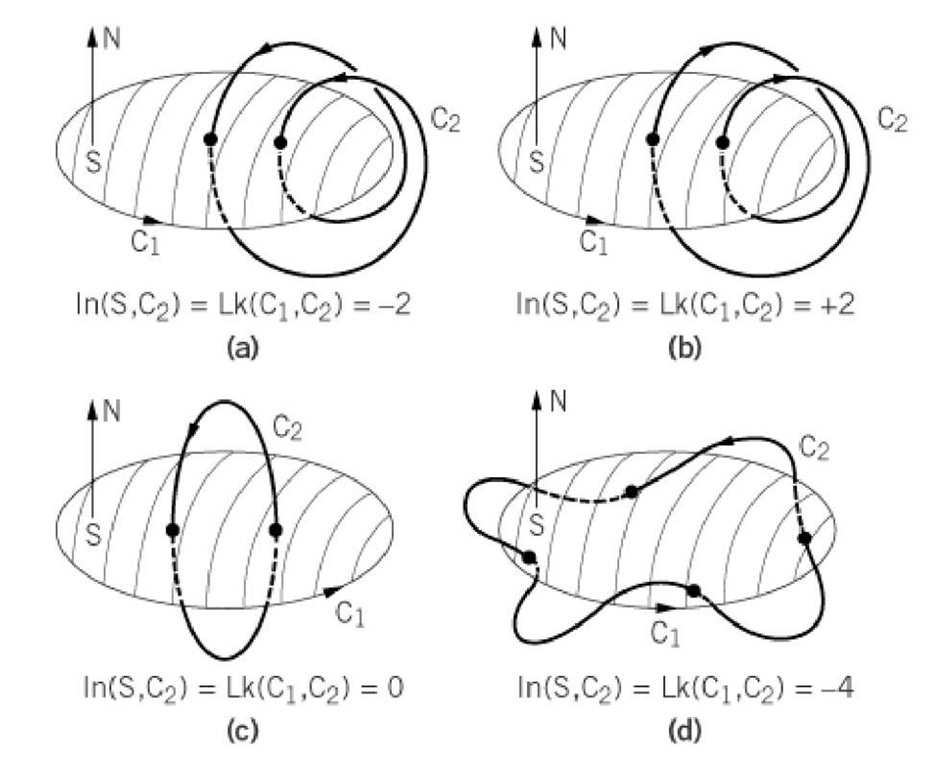
The second method of determining Lk is the surface intersection approach (1). Here either the DNA axis or one of the two strands is considered to form a spanning surface, which the other strand then repeatedly intersects. For an illustration of how to use the spanning surface to calculate Lk, refer to Figure 2. The surface is assigned an orientation; as shown in the figure, the surface normal is taken to be upward-pointing with the curve oriented counterclockwise, equivalent to following a right-hand rule. To each intersection is assigned an index of+1 or -1, depending on the direction of the intersection with respect to the surface orientation. By convention, the index number is positive if the tangent vector of the intersecting curve points along the direction of the surface normal and is negative for the opposite case. Lk is then the sum of these index numbers. An easily constructed spanning surface, as depicted in the figure, is that whose perimeter is formed by the axis of the closed circular DNA. For relaxed circular DNA, for example, this surface is approximately bounded by a circle. The surface intersection approach may also be employed with the other strand used to form the spanning surface. This choice of spanning surface more readily lends itself to calculation of Lk for complex cases in which the DNA axis is poorly defined locally. This occurs, for example, in the extrusion of a cruciform. As noted above, the linking number is the same for interstrand winding as for strand-axis winding.

Figure 2. Construction and use of the spanning surface in calculation of the linking number. The mathematical convention is followed in choosing the orientation of the curves; the arrows are pointed in the 5′ ^ 3′ direction for one strand and in the 3′ ^ 5′ direction for the other. The arrows are therefore oriented parallel to one another. One of the two strands is chosen to form the spanning surface, and direction of the normal to the surface is taken in the sense of the classic Stokes theorem; specifically, the right-hand rule is followed. Then the local contribution to the intersection number is +1 if the tangent to C at the intersection point is parallel to the surface normal. The contribution is -1 if the tangent to C at the intersection point is antiparallel to the surface normal. (a) Here the spanning surface is intersected twice in the antiparallel sense, and Lk = -2. (b) Here both intersections are in the parallel sense, and Lk = +2. (c) Here the two intersections are in the opposite sense and Lk = +1 – 1 = 0. (d) Here the surface is intersected four times in the antiparallel sense and Lk = 4.

2.3. The Gauss Integral Approach

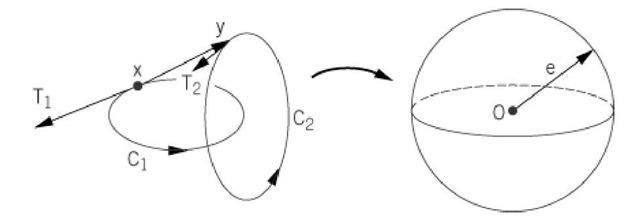
The third and most formal method of calculating Lk employs the Gauss integral. The integral is taken over all pairs of points on the two strands, which are again labeled C1 and C 2. A graphical description of the geometric quantities involved is given in Figure 3. The linking number is calculated from the integral (2).

where x is an arbitrary location on strand C1, y is an arbitrary point on strand C2; T1 is the unit tangent vector to C1 at x; and T2 is the unit tangent vector to C2 at y. The two curves are connected between any pair of these points by the vector y-x,whose scalar length is r = vbm0;y-xvbm0;. Then e; is the unit vector along r, and $\hatThe quantities s1 and s2 are the arc lengths on C1 at x and on C 2 at y. Because of its complexity, and because of the need for knowledge of the exact chain trajectory, the Gauss integral is impractical for the calculation of Lk for DNA. It is, however, useful for theoretical modeling purposes.

Figure 3. The Gauss map for calculation of the linking number. Here x is an arbitrary point on strand Cl andy is an arbitrary point on strand C 2. T1 is the unit tangent vector to strand C l at x, and T2 is the unit tangent vector to strand C2 aty. The unit vector aaceacacd4;aca = (y-x)/r, where r = vbm0;y-xvbm0;. If the unit vector e; is translated parallel to the origin, its terminus becomes a point on a sphere of unit radius, centered at the origin. Each pair of (x, y) points therefore maps to a unique point on this unit sphere. The Gauss integral for Lk measures how many times the e; vector sweeps across the surface of this sphere in a positive or negative sense. The factor 1 / 4p is the surface area of a unit sphere and normalizes the result to give the number of turns.

3. Linking Difference and Superhelix Density

3.1. Linking Difference

The linking difference applies to an elementary topological domain (see DNA Topology) and is a measure of the deviation in the winding of a cdDNA from that of its nonclosed circular counterpart. Consequently it is DLk, rather than just the linking number, Lk, that determines the chemically and biologically interesting properties of a topological domain. The linking difference is defined by the difference between Lk and the value of the pseudo-linking number for the corresponding nicked circular or linear DNA, LkQ. These latter species are termed, collectively, open duplex DNA:

In contrast to Lk, Lk0 is seldom an integer, even for completely purified cdDNA. Lk0 is related to the number of base pairs, N, and to the DNA helical repeat, ^ base pairs per turn, by

The local value of the B-DNA helical repeat is dependent on the base composition (3) and is different for noncanonical DNA structures, such as Z-DNA, H, and locally denatured DNAs. For the linear axis B form of DNA in dilute NaCl at 37°C, the average ^ = 10.5 base pairs/turn (4, 5).

3.2. Relaxed Duplex DNA

A nicked circular duplex DNA contains at least one backbone chain interruption. Such a DNA loses its topological domain, and free rotation about the chain scission takes place. In contrast to a nicked circular DNA, a relaxed duplex DNA (rdDNA) is that topoisomer whose linking number is the nearest integer to Lk 0. Since L^ itself is generally not an integer, the rdDNA species usually has a value of DM that is small and fractional. This fractional displacement * is simply the difference between the exact value of Lk{) from Equation (3) and the nearest integer, and -0.5 < * < 0.5. For example, pBR322 DNA has N= 4363,1,k{) = 415.52, and consequently * = -0.48. The rdDNA topoisomer is therefore the one with Lk = 416. Physically, e represents the minimum fractional rotation that is required in a nicked circular DNA, whose axis initially lies in a plane, to bring the 5′ and 3′ ends together in order to allow covalent joining by a DNA Ligase. The sign and magnitude of e can be determined experimentally from the Boltzmann distribution of topoisomers that forms on thermal equilibration in the presence of a topoisomerase. This distribution is well fit by a Gaussian curve in topoisomer frequency versus DLk, and e is the separation between the center of this distribution and the location of the nearest, most prominent topoisomer (6, 7) (see Superhelical DNA Energetics). A closed DNA is underwound if DLk < 6, which is the case for all naturally occurring closed circular DNAs. The linking difference is consequently sometimes called the linking deficiency, although linking excess would be the appropriate term for cases in which the DNA is overwound, or DLk > E. The DNA is said to be relaxed if DLk = 6, even though it might still contain a small linking difference.

Both the sign and the magnitude of DLk can be altered by changing either Lk or Lk^. The former can be changed by treatment with DNA topoisomerase, DNA gyrase, or reverse DNA gyrase; the latter can be changed by altering the salt type or concentration (8), the temperature (6, 9), or by the addition of an intercalating drug (10). Thus, a relaxed duplex DNA can be made to supercoil by a change in its environment alone. For comparison purposes, it is therefore necessary to specify the conditions under which L^ is measured. The usual standard state is 37°C, 0.2 MNaCl, and no added reagents that change the DNA twist (11). If necessary, the value of Lk 0 under standard conditions can be specified as Lk^^.

3.3. Superhelix Density

All other things being equal, Lk, Lk^, and DLk are proportional to the DNA length. In order to compare two DNA molecules of different lengths, it is convenient to define the associated normalized quantity, the superhelix density or specific linking difference, s. The superhelix density is defined by

Although the term "superhelix" is traditionally used here, it should not be taken to imply any specific tertiary structure (see DNA Topology). Most naturally occurring cdDNAs have values of s between 0 and -0.1 under standard conditions, but DNAs having s as great as -0.17 have been prepared in vitro (12). cdDNA of relatively large positive s values have been prepared with the DNA reverse gyrase (13). Since both s and Lk 0 are readily accessible experimental quantities, the practical way to calculate Lk is by combining Lk0 with the measured value of either DLk or s. To continue the example of pBR322 DNA, with N = 4363 and ^ = 10.5 base pairs/turn, the DNA occurs naturally with an average value of s = -0.06. Taking this number to be exact for purposes of illustration, the average linking number for this native DNA is then 390.58. The linking number of the nearest (most prevalent) topoisomer is 391.

As with DLk, s can be varied by changes in environmental conditions alone, even with no change in Lk. For example, the temperature coefficient of s is Ds/DT = 3.1*10-4deg-1. If the temperature is changed from 5 to 37°C, the change in s is +0.01. For pBR322 DNA, this changes DLk by +4.16 turns. An increase in temperature thus causes a relaxed DNA to supercoil in the positive sense (a left-handed, interwound superhelix) and reduces the supercoiling of a naturally occurring (underwound) superhelical DNA. Similar effects result from changing the cation species and concentration (8). Over the ionic strength range 0.05-0.3 M, Ds/DpX = 4.47*10 for the ions Na , K+, Li+, and NH+4 and Ds/DpX+ = 6.70*10-3 for Rb+, Cs+, and Mg2+, where pX+ is the negative logarithm of the cation concentration. For example, if the sodium ion concentration is decreased from 1.0 to 0.01 M, the change in s is +0.013 and is comparable to a temperature increase of 42°C. Both these effects are clearly evident in gel electrophoreses experiments under the appropriate different conditions.

4. Relationship of DNA Topology to DNA Geometry

In spite of its being topological (nonmetric), the linking number is equal to the sum of two very important DNA geometric properties (14): the twist, Tw, and the writhe, Wr:

This equation is fundamental to understanding any topological domain in DNA. An immediate consequence of this relationship is that, for any process in which Lk is unchanged, any changes in the twist are matched exactly by changes in the writhe (but of opposite sign):

The linking difference also appears in a modified version of the fundamental relationship for a topological domain, Equation (5). A nicked circular DNA has no writhe, so Tw0 = Lk^. Combining this condition with Equation (5) gives

Here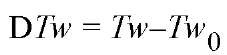represents the deviation of the twist from the open circular (B-DNA solution) value. Equation (7) points to two differences between a relaxed duplex DNA and a nicked circular duplex DNA. The first difference is relatively minor. The nicked circular duplex DNA has Wr = DTw = 0, but for the relaxed duplex DNA Wr+DTw = r. That is, a relaxed duplex DNA may be slightly distorted by some combination of changes in Tw and Wr. Theoretical calculations indicate that all the distortion goes into twist for a perfect elastic rod (15, 16) but that it all goes to writhe for any actual case involving DNA (J. H. White, submitted). The second difference is major. In a rdDNA the twist and writhe remain coupled, such that dDTw = -dWr. For a nicked circular DNA, however, D Lk is not defined and Equation (7) does not apply. In this case, DTw and Wr are uncoupled and may fluctuate independently. These differences explain why nicked circular DNA often migrates more slowly than relaxed circular DNA in both gel electrophoresis and sedimentation experiments, even under identical solution conditions.