2.2
The computer is often used to compute numerical data, as the name implies, or to keep topics or control machinery. These operations need arithmetic instructions, which we now study. However, you must recall that computers are designed and programs are written to enhance static or dynamic efficiency. Rather than have the four basic arithmetic instructions that you learned in grade school —add, subtract, multiply, and divide—computers have the instructions that occur most often in programs. Rather than having the sophisticated square root as an instruction, for instance, we will see the often-used increment instruction in a computer. Let us look at them. See Table 2.4.
We have already discussed the add instructions: ADCA, ADCB, ADDA, ADDB, and ADDD. The corresponding subtraction instructions, SBC A, SBCB, SUBA, SUBB, and SUBD, are the obvious counterparts of add instructions, where the carry condition code bit holds the borrow. However, 16-bit add and subtract instructions with carry. ADCD and SBCD. are missing; multiple-byte arithmetic must be done one byte at a time rather than two bytes at a time. Comparisons are normally made by subtracting two numbers and checking if the result is zero, negative, positive, or a combination of these. But using the subtract instruction to compare a fixed number against many numbers requires that the fixed number has to be reloaded in the register each time the subtraction is performed. To streamline this process, compare instructions are included that do not change the contents of the register used. These compare instructions are used to compare the contents of registers A, B, D, X. Y, and SP with the contents of memory locations in order to give values to the condition code bits C, V, N, and Z. Finally, note that DEC. INC. and NEG are provided for often-used special cases of add and subtract instructions, to improve efficiency.
Table 2.4. Add Instructions Using an Effective Address
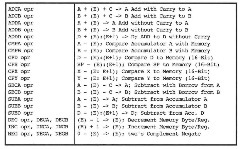

Figure 2.5. Program Segment for 32-Bit Addition
Figure 2.5 illustrates a simple example of an arithmetic operation: adding a 4-byte number at $850 to a 4-byte number at $854. ADDD can be used to add the two low-order bytes, but ADCB and ADCA are needed to add the high-order bytes.
Arithmetic instructions are really very simple and intuitively obvious, except for the condition code bits. Addition or subtraction uses the same instruction for unsigned as for two’s-complement numbers, but the test for overflow is different (see Appendix 1). The programmer has to use the correct condition code test after instruction completion; for example, SUBA $876 sets C = 1 if, and only if, there has been an unsigned overflow; that is, A – ($876) produces a borrow or, when each number is treated as an unsigned number, A < ($876). (Here A and ($876) denote the contents of A and the contents of location $876.) Similarly, V = 1 if, and only if, a two’s-complement (signed) overflow occurs, when A and ($876) are treated as two’s-complement numbers; i.e., A – ($876) is not in the 8-bit two’s-complement range. Note again that subtraction is performed with the same instruction, such as SUBA f regardless of whether the numbers are two’s-complement or unsigned numbers.
Table 2.5 shows special instructions used to improve efficiency for commonly used operations. ABX, ABY, ABA, CBA, and SBA use accumulator B, and DBS, DEX, DEY, INS , INX, and I NY increment or decrement index registers and the stack pointer.
Multiply instructions MUL and EMUL multiply unsigned numbers in specific registers. EMULS similarly multiplies signed numbers. One may also multiply a signed or unsigned number by two with the arithmetic shift-left instructions discussed with the edit class, such as ASLA, ASLB, ASLD, and ASL 527. Divide instructions IDIV, FDIV, and EDIV divide unsigned numbers in specific registers. IDIVS similarly divides signed numbers. One may divide a two’s-complement number by two with corresponding arithmetic shift-right instructions, e.g., ASRA, ASRB, and ASR 327.
![]()
Figure 2.6. Multiplication
Table 2.5. Arithmetic Instructions That Do Not Use an Effective Address

Multiplication can be done by addition and shifting almost as multiplication is done by hand, but to save hardware, the product is shifted rather than shifting the multiplier to be added to it. Figure 2.6 multiplies a 4-bit unsigned number 0110 by another 4-bit number 1010, to get an 8-bit product. First, because the most significant bit of the multiplier 1010 is one, add the number 0110 into the initial product 0. then shift the product one bit left, twice, and then add the number 0110 into the product, and shift the product one bit left. The answer is 00111100.
Actually, modern microcontrollers execute several shift-and-add operations in one clock cycle. Thus, EMUL, which multiplies a 16-bit by a 16-bit unsigned number, takes only three clock cycles. Signed multiplication sign extends its multiplier rather than filling with zero, and it treats the sign bit differently. Therefore use the EMULS instruction for signed numbers. These remarks apply analogously to the division instructions EDIV and EDIVS. The other instructions: EDIV, EDIVS, EMULS, FDIV, IDIV, IDIVS, and MUL, are similarly used. Note that after division, the remainder is in

Figure 2.7. Program Segment for 16-Bit Unsigned Multiplication

Figure 2.8. Program Segment for BCD Addition
accumulator D, and the quotient is in an index register. As an example of a multiplication of two 16-bit unsigned numbers at $852 and $854 to get a 16-bit product into $856, see Figure 2.7.
The special instruction, DAA (decimal adjust accumulator A), adds binary-coded decimal numbers. Briefly, two decimal digits per byte are represented with binary-coded decimal, the most significant four bits for the most significant decimal digit and the least significant four bits for the least significant decimal digit. Each decimal digit is represented by its usual 4-bit binary code, so the 4-bit sequences representing 10 through 15 are not used. To see how the decimal adjust works, consider adding a four-digit binary coded decimal number in the two bytes at $873 to a similar number at $862, as shown in Figure 2.8. DAA “corrects” ADDA’s result. The DAA instruction may be used after ADDA or ADCA but can’t be used with any other instructions such as ADDB, DECA, or SUBA.
Our next example illustrates the use of arithmetic instructions, with a move instruction to put the desired intermediate result in the correct register for the next operation. This example involves conversion of temperature from Celsius to Fahrenheit. If temperature T is measured in degrees Celsius, then the temperature in Fahrenheit is ((T * 9) / 5) + 32. Suppose T, a signed 16-bit number representing degrees Celsius, is in accumulator D. The program in Figure 2.9 evaluates the formula and leaves the temperature, in Fahrenheit, in accumulator D.

Figure 2.9. Program Segment for Conversion from Celsius to Fahrenheit
Arithmetic Instructions (Microcontrollers)
Next post: Logic Instructions (Microcontrollers)
Previous post: Move Instructions (Microcontrollers)
