19.21.
Sampling inspection techniques are used to estimate the lot quality for lot acceptance purposes. As already pointed out, 100% inspection (or screening) is not at all economical and in some cases it is impossible ; whereas the sampling inspection is generally more practical, quick, economical, and provides incentive to the producer to improve his quality as the rejection of a sample means rejection of the whole lot.
Table 19.9. Summation of Terms of Poisson’s Exponential Bionomial Limit 1,000 x probability of c or less occurrences of event that has average number of occurrences equal to e’ or np’
| c -» c or np’ I | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.02 | 980 | 1000 | ||||||||
| 0.04 | 961 | 999 | 1000 | |||||||
| 0.06 | 942 | 998 | 1000 | |||||||
| 0.08 | 923 | 997 | 1000 | |||||||
| 0.10 | 905 | 995 | 1000 | |||||||
| 0.15 | 861 | 990 | 999 | 1000 | ||||||
| 0.20 | 819 | 982 | 999 | 1000 | ||||||
| 0.25 | 779 | 974 | 998 | 1000 | ||||||
| 0.30 | 741 | 963 | 996 | 1000 | ||||||
| 0.35 | 705 | 951 | 994 | 1000 | ||||||
| 0.40 | 670 | 938 | 992 | 999 | 1000 | |||||
| 0.45 | 638 | 925 | 989 | 999 | 1000 | |||||
| 0.50 | 607 | 910 | 986 | 998 | 1000 | |||||
| 0.55 | 577 | 894 | 982 | 998 | 1000 | |||||
| 0.60 | 549 | 878 | 977 | 997 | 1000 | |||||
| 0.65 | 522 | 861 | 972 | 996 | 999 | 1000 | ||||
| 0.70 | 497 | 844 | 966 | 994 | 999 | 1000 | ||||
| 0.75 | 472 | 827 | 959 | 993 | 999 | 1000 | ||||
| 0.80 | 449 | 809 | 953 | 991 | 999 | 1000 | ||||
| 0.85 | 424 | 791 | 945 | 989 | 998 | 1000 | ||||
| 0.90 | 407 | 772 | 937 | 987 | 998 | 1000 | ||||
| 0.95 | 387 | 754 | 929 | 984 | 997 | 1000 | ||||
| 1.00 | 368 | 736 | 920 | 981 | 996 | 999 | 1000 |
![]()
Since the value is less than 2.583.
The pieces manufactured by first machine are not bigger than those manufactured by 2nd machine.
19.31.2.
Paired t-Test.
This test is applied to determine whether or not there is a significant difference between the means of two related lots. Such a situation arises when two samples are so given that the observations of one sample correspond to the observations of the other.
For this test, the differences between observations in each pair are found out; (the null hypothesis for such a case is that the mean of the difference is zero); and the t-test applied on these differences as if testing of the mean of these against zero.
Thus in case of two machines set to produce cylindrical plugs at a specified diameter, if the observations of two lots are quite close to each other, then this test is applied as under :

If this value is less than the critical value of t found from Table 19.18 for critical values of ^-distribution for 5% significance level from two-sided or one-sided as the case may be with n – 1 degrees of freedom, then it is presumed that the means of the two lots are same or in other words, the nuLUiypothesis that the average of the two lots does not differ with each other is not questioned.
Note.
It may be noted that the £-test is applied when the sample size is small and the information about the standard deviation is not available and, therefore, inferences are made
| c -» c or np’ I |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.1 | 333 | 699 | 900 | 974 | 995 | 999 | 1000 | |||
| 1.2 | 301 | 663 | 879 | 966 | 992 | 998 | 1000 | |||
| 1.3 | 273 | 627 | 857 | 957 | 989 | 998 | 1,000 | |||
| 1.4 | 247 | 592 | 833 | 946 | 986 | 997 | 999 | 1,000 | ||
| 1.5 | 223 | 558 | 809 | 934 | 981 | 996 | 999 | 1,000 | ||
| 1.6 | 203 | 525 | 783 | 921 | 976 | 994 | 999 | 1,000 | - | |
| 1.7 | 183 | 493 | 757 | 907 | 970 | 992 | 998 | 1,000 | ||
| 1.8 | 165 | 463 | 731 | 891 | 964 | 990 | 997 | 999 | 1,000 | |
| 1.9 | 150 | 434 | 704 | 875 | 956, | 987 | 997 | 999 | 1,000 | |
| 2.0 | 135 | 406 | 677 | 857 | 947 | 983 | 995 | 999 | 1,000 | |
| 2.2 | 111 | 335 | 623 | 819 | 928 | 975 | 993 | 998 | 1,000 | |
| 2.4 | 091 | 308 | 570 | 779 | 904 | 964 | 988 | 997 | 999 | 1,000 |
| 2.6 | 074 | 267 | 518 | 736 | 877 | 951 | 983 | 995 | 999 | 1,000 |
| 2.8 | 061 | 231 | 469 | 692 | 948 | 935 | 976 | 992 | 998 | 999 |
| 3.0 | 050 | 199 | 423 | 647 | 815 | 916 | 966 | 988 | 996 | 999 |
| 3.2 | 041 | 171 | 380 | 603 | 781 | 895 | 955 | 983 | 994 | 998 |
| 3.4 | 033 | 147 | 340 | 558 | 744 | 871 | 944 | 977 | 992 | 997 |
| 3.6 | 027 | 126 | 303 | 515 | 706 | 844 | 927 | 969 | 988 | 996 |
| 3.8 | 022 | 107 | 269 | 473. | 668 | 816 | 909 | 960 | 984 | 994 |
| 4.0 | 018 | 092 | 238 | 433 | 629 | 785 | 889 | 949 | 979 | 992 |
| 4.2 | 015 | 078 | 210 | 395 | 590 | 753 | 867 | 936 | 972 | 989 |
| 4.4 | 012 | 066 | 185 | 359 | 551 | 720 | 844 | 921 | 964 | 985 |
| 4.6 | 010 | 056 | 163 | 326 | 513 | 686 | 818 | 905 | 955 | 980 |
| 4.8 | 008 | 048 | 143 | 294 | 476 | 651 | 791 | 887 | 944 | 975 |
| 5.0 | 007 | 040 | 125 | 265 | 440 | 616 | 762 | 867 | 932 | 968 |
| 5.2 | 006 | 034 | 109 | 238 | 406 | 581 | 732 | 845 | 918 | 960 |
| 5.4 | 005 | 029 | 095 | 213 | 373 | 546 | 702 | 822 | 903 | 951 |
| 5.6 | 004 | 024 | 082 | 191 | 342 | 512 | 670 | 797 | 886 | 941 |
| 5.8 | 003 | 021 | 072 | 170 | 313 | 478 | 638 | 771 | 867 | 929 |
| 6.0 | 002 | 017 | 062 | 151 | 285 | 446 | 606 | 744 | 847 | 916 |
| C-» | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |||
| 2.8 | 1,000 | |||||||||
| 3.0 | 1,000 | |||||||||
| 3.2 | 1,000 | |||||||||
| 3.4 | 999 | 1,000 | ||||||||
| 3.6 | 999 | 1,000 | ||||||||
| 3.8 | 998 | 999 | 1,000 | |||||||
| 4.0 | 997 | 999 | 1,000 | |||||||
| 4.2 | 996 | 999 | 1,000 |
| c -» c or rap’ 1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||||
| 4.4 | 994 | 998 | 999 | 1,000 | |||||||||||||||||
| 4.6 | 992 | 997 | 999 | 1,000 | |||||||||||||||||
| 4.8 | 990 | 996 | 999 | 1,000 | |||||||||||||||||
| 5.0 | 986 | 995 | 998 | 999 | 1,000 | ||||||||||||||||
| 5.2 | 982 | 993 | 997 | 999 | 1,000 | ||||||||||||||||
| 5.4 | 977 | 990 | 996 | 999 | 1,000 | ||||||||||||||||
| 5.6 | 972 | 988 | 995 | 998 | 999 | 1,000 | |||||||||||||||
| 5.8 | 965 | 984 | 993 | 997 | 999 | 1,000 | |||||||||||||||
| 6.0 | 957 | 980 | 991 | 996 | 999 | 999 | 1,000 | ||||||||||||||
| 6.2 | 002 | 015 | 054 | 134 | 259 | 414 | 574 | 756 | 826 | 902 | |||||||||||
| 6.4 | 002 | 012 | 046 | 119 | 235 | 384 | 542 | 687 | 803 | 886 | |||||||||||
| 6.6 | 001 | 010 | 040 | 105 | 213 | 355 | 511 | 658 | 780 | 869 | |||||||||||
| 6.8 | 001 | 009 | 034 | 093 | 192 | 327 | 480 | 623 | 755 | 850 | |||||||||||
| 7.0 | 001 | 007 | 030 | 082 | 173 | 103 | 450 | 599 | 729 | 830 | |||||||||||
| 7.2 | 001 | O06 | 025 | 072 | 156 | 276 | 420 | 569 | 703 | 810 | |||||||||||
| 7.4 | 001 | 005 | 022 | 063 | 140 | 253 | 392 | 539 | 679 | 788 | |||||||||||
| 7.6 | 001 | 004 | 019 | 055 | 125 | 231 | 365 | 510 | 648 | 765 | |||||||||||
| 7.8 | 000 | 004 | 016 | 048 | 112 | 210 | 338 | 481 | 620 | 741 | |||||||||||
| 8.0 | 000 | 003 | 014 | 042 | 100 | 191 | 313 | 453 | 593 | 717 | |||||||||||
| 8.5 | 000 | 002 | 009 | 030 | 074 | 150 | 256 | 386 | 523 | 653 | |||||||||||
| 9.0 | 000 | 001 | 006 | 021 | 055 | 116 | 207 | 324 | 456 | 587 | |||||||||||
| 9.5 | 000 | 001 | 004 | 015 | 040 | 089 | 165 | 269 | 392 | 522 | |||||||||||
| 10.0 | 000 | 000 | 003 | 010 | 029 | 067 | 130 | 220 | 333 | 458 | |||||||||||
| c -> | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | ||||||||
| 6.2 | 949 | 975 | 989 | 995 | 998 | 999 | 1,000 | ||||||||||||||
| 6.4 | 939 | 969 | 986 | 994 | 997 | 999 | 1,000 | ||||||||||||||
| 6.6 | 927 | 963 | 982 | 992 | 997 | 999 | 999 | 1,000 | |||||||||||||
| 6.8 | 915 | 955 | 978 | 990 | 996 | 998 | 999 | 1,000 | |||||||||||||
| 7.0 | 901 | 947 | 974 | 987 | 994 | 998 | 999 | 1,000 | |||||||||||||
| 7.2 | 887 | 937 | 967 | 984 | 993 | 997 | 999 | 999 | 1,000 | ||||||||||||
| 7.4 | 871 | 926 | 961 | 980 | 991 | 996 | 998 | 999 | 1,000 | ||||||||||||
| 7.6 | 854 | 915 | 954 | 976 | 989 | 995 | 998 | 999 | 1,000 | ||||||||||||
| 7.8 | 835 | 902 | 945 | 971 | 986 | 993 | 997 | 999 | 1,000 | ||||||||||||
| 8.0 | 816 | 888 | 936 | 966 | 983 | 992 | 996 | 998 | 999 | 1,000 | |||||||||||
| 8.5 | 763 | 849 | 909 | 949 | 973 | 989 | 993 | 997 | 999 | 999 | 1,000 | ||||||||||
| 9.0 | 706 | 803 | 876 | 926 | 959 | 978 | 989 | 995 | 998 | 999 | 1,000 | ||||||||||
| 9.5 | 645 | 752 | 836 | 838 | 940 | 967 | 982 | 991 | 996 | 999 | 999 | 1,000 | |||||||||
| 10.0 | 583 | 697 | 792 | 864 | 917 | 951 | 973 | 986 | 993 | 997 | 998 | 999 | 1,000 | ||||||||
| C -¥ c or np’ I |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10.5 | 000 | 000 | 002 | 007 | 021 | 050 | 102 | 179 | 279 | 397 |
| 11.0 | 000 | 000 | 001 | 005 | 015 | 038 | 079 | 143 | 232 | 341 |
| 11.5 | 000 | 000 | 001 | 003 | Oil | 028 | 060 | 114 | 191 | 289 |
| 12.0 | 000 | 000 | 001 | 002 | 008 | 020 | 046 | 090 | 155 | 242 |
| 12.5 | 000 | 000 | 000 | 002 | 005 | 015 | 035 | 070 | 125 | 201 |
| 13.0 | 000 | 000 | 000 | 001 | 004 | Oil | 026 | 054 | 100 | 166 |
| 13.5 | 000 | 000 | 000 | 001 | 003 | 006 | 019 | 041 | 079 | 135 |
| 14.0 | 000 | 000 | 000 | 000 | 002 | 006 | 014 | 032 | 062 | 109 |
| 14.5 | 000 | 000 | 000 | 000 | 001 | 004 | 010 | 024 | 048 | 088 |
| 15.0 | 000 | 000 | 000 | 000 | 001 | 003 | 008 | 018 | 037 | 070 |
| c -* ci |
10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 10.5 | 521 | 639 | 742 | 825 | 888 | 932 | 960 | 978 | 988 | 994 |
| 11.0 | 460 | 579 | 689 | 781 | 854 | 907 | 944 | 968 | 982 | 991 |
| 11.5 | 402 | 520 | 633 | 733 | 815 | 878 | 924 | 954 | 974 | 986 |
| 12.0 | 347 | 462 | 576 | 682 | 772 | 844 | 899 | 937 | 963 | 979 |
| 12.5 | 296 | 406 | 519 | 628 | 725 | 806 | 869 | 916 | 948 | 969 |
| 13.0 | 252 | 353 | 463 | 573 | 675 | 764 | 835 | 890 | 930 | 957 |
| 13.5 | 211 | 304 | 409 | 518 | 623 | 718 | 798 | 861 | 908 | 942 |
| 14.0 | 176 | 260 | 358 | 464 | 570 | 669 | 756 | 827 | 883 | 923 |
| 14.5 | 145 | 220 | 311 | 413 | 518 | 619 | 711 | 790 | 853 | 901 |
| 15.0 | 118 | 185 | 268 | 363 | 466 | 568 | 664 | 749 | 819 | 875 |
| c -> cl | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 10.5 | 997 | 999 | 999 | 1,000 | ||||||
| 11.0 | 995 | 998 | 999 | 1,000 | ||||||
| 11.5 | 992 | 996 | 998 | 999 | 1,000 | |||||
| 12.0 | 988 | 994 | 997 | 999 | 999 | 1,000 | ||||
| 12.5 | 983 | 991 | 995 | 998 | 999 | 999 | 1,000 | |||
| 13.0 | 975 | 986 | 992 | 996 | 999 | 999 | 1,000 | 1,000 | ||
| 13.5 | 965 | 980 | 989 | 994 | 997 | 998 | 999 | 1,000 | ||
| 14.0 | 952 | 971 | 983 | 991 | 995 | 997 | 999 | 999 | 1,000 | |
| 14.5 | 936 | 960 | 976 | 986 | 992 | 996 | 999 | 998 | 999 | 1,000 |
| 15.0 | 916 | 947 | 967 | 981 | 989 | 994 | 997 | 997 | 999 | 1,000 |
| c -> c or np’ I | 0 | 1 | 2 | 3 | 4 | 5 | CO | 7 | 8 | 9 |
| 16 | 000 | 000 | 004 | 010 | 022 | 043 | 077 | 127 | 193 | 275 |
| 17 | 000 | 000 | 002 | 005 | 013 | 026 | 049 | 085 | 135 | 201 |
| 18 | 000 | 000 | 001 | 003 | 007 | 015 | 030 | 055 | 092 | 143 |
| 19 | 000 | 000 | 001 | 002 | 004 | 009 | 018 | 035 | 061 | 098 |
| 20 | 000 | 000 | 000 | 001 | 002 | 005 | 001 | 021 | 039 | 066 |
| 21 | 000 | 000 | 000 | 000 | 001 | 003 | 006 | 013 | 025 | 043 |
| 22 | 000 | 000 | 000 | 000 | 000 | 002 | 004 | 008 | 015 | 028 |
| 23 | 000 | 000 | 000 | 000 | 000 | 000 | 002 | 004 | 009 | 017 |
| 24 | 000 | 000 | 000 | 000 | 000 | 000 | 001 | 003 | 005 | Oil |
| 25 | 000 | 000 | 000 | 000 | 000 | 000 | 001 | 001 | 003 | 006 |
| c -» ci | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 16 | 368 | 467 | 566 | 659 | 742 | 812 | 868 | 911 | 942 | 963 |
| 17 | 281 | 371 | 468 | 664 | 655 | 736 | 805 | 861 | 905 | 937 |
| 18 | 208 | 287 | 375 | 469 | 562 | 651 | 731 | 799 | 855 | 899 |
| 19 | 150 | 215 | 292 | 378 | 469 | 561 | 647 | 725 | 793 | 849 |
| 20 | 105 | 157 | 221 | 297 | 381 | 470 | 559 | 644 | 721 | 787 |
| 21 | 072 | Oil | 163 | 227 | 302 | 384 | 471 | 558 | 640 | 716 |
| 22 | 048 | 077 | 117 | 169 | 232 | 306 | 387 | 472 | 556 | 637 |
| 23 | 031 | 052 | 082 | 123 | 175 | 238 | 310 | 389 | 472 | 555 |
| 24 | 020 | 034 | 056 | 087 | 128 | 180 | 243 | 314 | 392 | 473 |
| 25 | 012 | 022 | 038 | 060 | 092 | 134 | 185 | 247 | 318 | 394 |
| c -> c4- | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| 16 | 978 | 987 | 993 | 996 | 998 | 999 | 999 | 1,000 | ||
| 17 | 959 | 975 | 985 | 991 | 995 | 997 | 999 | 999 | 1,000 | |
| 18 | 932 | 955 | 972 | 983 | 990 | 994 | 997 | 998 | 999 | 1,000 |
| 19 | 895 | 927 | 951 | 969 | 980 | 988 | 993 | 996 | 998 | 999 |
| 20 | 843 | 888 | 922 | 948 | 966 | 978 | 987 | 992 | 995 | 997 |
| 21 | 782 | 838 | 883 | 917 | 944 | 963 | 976 | 985 | 991 | 994 |
| 22 | 712 | 777′ | 832 | 877 | 913 | 940 | 959 | 973 | 983 | 989 |
| 23 | 635 | 708 | 772 | 827 | 873 | 908 | 936 | 956 | 971 | 981 |
| 24 | 554 | 632 | 704 | 768 | 823 | 868 | 904 | 932 | 953 | 969 |
| 25 | 472 | 553 | 629 | 700 | 763 | 818 | 863 | 900 | 929 | 950 |
| c -> ci | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
| 19 | 999 | 1,000 | ||||||||
| 20 | 999 | 999 | 1,000 | |||||||
| 21 | 997 | 998 | 999 | 999 | 1,000 | |||||
| 22 | 994 | 995 | 998 | 999 | 999 | 1,000 | ||||
| 23 | 988 | 993 | 996 | 997 | 999 | 999 | 1,000 | |||
| 24 | 979 | 987 | 992 | 995 | 997 | 998 | 999 | 999 | 1,000 | |
| 25 | 966 | 977 | 985 | 991 | 994 | 997 | 998 | 999 | 999 | 1,000 |
According to the method of inspection, the quality (i.e., the characteristic of interest) of a product or material can be broadly classified as (i) attributes, (ii) count of defects, (Hi) variables. In the method of classification by attributes, each item inspected is classified as satisfying one particular characteristic or not, e.g., ininspection by gauges-either a component is satisfactory or not. In inspection by attributes, the object is to limit the number of items having one or more defects. In second method (count of defects), and number of defects on each inspected item are counted and it is carried out when the object is to limit the average number of defects in the items. In the method of classification by variables, the characteristic is measured on a continuous scale. For these three methods of quality classification, the lot quality is described respectively in terms of (i) percentage defective, (ii) number of defects per item or for 100 items, (Hi) arithmetic mean or standard deviation or both, or coefficient of variation which is the ratio of the standard deviation to the average.
19.21.1.
Whether to go for attributes inspection, or inspection by variables.
Whenever there is a choice to decide which of the two methods of inspection should be followed, the following considerations may be looked for :
| Consideration | Attributes Inspection | Inspection by variables | |
| (i) | Cost of inspection | Since it involves use of GO or NO GO gauges, inspection cost is low. | Measurement of any characteristic by measuring instruments involves more time and labour and thus cost. It also involves more record keeping and calculations for computation of mean, standard deviation etc. |
| (ii) | Items to be inspected for the same degree of efficiency in drawing inference about the lot. | More | Less. This method is, therefore, suited in case were destructive or costly testing is involved. |
| (iii) | Method of estimating the sample quality from the item quality. | Less complicated | More complicated. |
| (iv) | Information furnished | It does not give much information | It gives much more information about the quality of item lot. |
| (v) | Assumptions | No. Therefore, more applications | Characteristics, under consideration should have normal distribution. |
| (vi) | Limitations | No. Many characteristics can be considered at a time to classify an item as defective or non-defective. | Only one characteristics can be considered at a time. |
| (vii) | General | Inspection is slightly subjective, i.e. items of border-line quality may be classified as defective or non-defective depending on the sense of the operator. | Inspection is more objective. As it involves taking actual measurements, it minimises the possibilities of inspection bias and error. |
19.21.2.
Principles of Sample Selection.
It has been realised in most of the industrial and trade applications that 100% inspection (checking) and testing of components is not feasible and the sampling procedures have become indispensable tools because of their economy, reliability and practicability. However, the reliability of the conclusions drawn (e.g.,
estimating the quality of a lot or ascertaining its conformity to the requirements of a specification) on the basis of the sample depends on its representativeness and the method of its selection. The method of sampling adopted should be such that it ensures a truly random and representative sample leading to sound and satisfactory estimation of lot quality. Bureau of Indian Standards has prepared a specification (IS : 4905-1968 Methods for Random Sampling) to achieve this objective.
It may be understood that in the lot sampling, the inference about the lot is drawn on the basis of information given by a sample, and there is every possibility that the sample may not be true representative of the lot because out of any lot many samples can be made and all the samples cannot be identical. Thus there are chances that a bad lot may be accepted or good lot may be rejected ; the error on this account is known as the sampling error. Similarly when lot sampling is being carried out to estimate the lot quality then due to sampling error the sample estimate may be different from the actual value of the lot quality.
The sampling error depends upon :
(i) the degree of homogeneity of the lot, (ii) the size of the sample, (iii) method of sample selection.
It may be stressed here that the method of sampling adopted should be such that it avoids bias of any form (i.e., giving preference to certain positions in the lot, intentionally choosing either defectives or non-defectives only, unplanned sampling). Method of random sampling (in which the chance for inclusion of any items in the sample is predetermined and is independent of the quality of the item and is also independent of the quality of other items selected for the sample) avoids all types of biases.
For random selection, if possible, the lot should be thoroughly mixed, sample units selected blindly from all parts of the lot, the various parts so arranged that sampler has access to all, the position of selection of sample unit in each part being changed.
The method of simple random sampling can be followed if the lot consists of a number of items such that each item is easily identifiable and, apart from the lot size, all other information about the composition of the lot is available. According to this method, once an item has been drawn, it will not be put back into the lot till complete sampling is over. IS : 4950-1968 gives a table of random numbers containing 3000 digits (from 0 to 9), arranged randomly in 15 pages. For convenience of reading, the digits have been grouped into sets of 5 and arranged in 40 rows and 50 columns at each page. All the items in a lot are numbered at random and then the item numbers to be selected from the lot to form a random sample are found out from this table. The random numbers are selected by choosing any page and starting at random from any place vertically downwards. The digits greater than the lot size may be ignored.
19.21.3.
Methods of Random Sampling. Other methods of sampling include :
(i) Systematic sampling.
(ii) Stratified sampling. (iii) Cluster sampling. (iv) Sampling in stages.
Method of systematic sampling is applicable to cases where the items are presented in an orderly manner and the sample units are chosen at regular intervals. Here it is assumed that there is no deliberate attempt to manipulate the sequence of the items in the lot in any desired manner while the lot is presented for inspection.
In the method of systematic sampling, first a single sample item is selected from the lot of N items at random and then the items are selected at regular predetermined intervals (of N/n) to make up the desired sample of size n.
The method of stratified sampling is possible where the lot can be sub-divided into a certain number or more homogeneous groups or strata and then each stratum sampled separately. As this method draws items from each stratum of the lot, the sample drawn by this method is considered to be more representative of the lot.
The division of a lot into the strata may be on the basis of the homogeneity of the items within a lot, or convenience of sampling, or such other considerations which would make the item within each stratum as much alike as possible. The number of items selected from each stratum are proportional to the size of the stratum, ensuring that at least two items are drawn from each stratum.
When the lot submitted for inspection consists of certain groups of clusters of items, {e.g., when a lot consists of items packed in cartons and it is either impracticable or costly to repack the cartons opened for selecting sample items) it is advisable to go in for cluster sampling method. In this method, first a few clusters are selected and then all the items are inspected in the selected clusters. The results of this method will be satisfactory only if the items within a cluster are quite heterogeneous.
In cases where the lot is in the form of packages and it is impossible to take sample from each package after opening it, then first some packages are selected at random and then from each package a random sample of items proportional to the size of the package is chosen. This method is known as sampling in stages. In this method, in the first stage, a desired number of primary units are selected at random and in the second stage, the required number of items are chosen at random from the selected primary units.
19.21.4.
Planning sample selection.
Proper planning of the sample selection is very important to satisfy the assumptions made in sample theory and to achieve the maximum possible sampling efficiency. For this purpose it is desirable that the maximum possible information be gathered about the lot, the nature of items and the quality characteristics etc. Some of the important points requiring due considerations are discussed below :
(i) We should be clear about the purpose for which the sample has to be selected, i.e. whether for assessing the quality of the lot, or for lot acceptance. It may be noted that though the method of sampling will be same for both the purposes, the size of the sample will be different in two cases.
(ii) The next important step is the formation of lots, for which due consideration has to be given to the nature of the lot, i.e. stationary lot or moving lot, item lot or bulk lot, homogeneity of lot, formation of sub-lots etc.
It may be emphasised that for inspection purposes, a lot is viewed as an aggregate of items which may be in the form of a batch, a group, a continuous stream or a bulk of products of raw materials.
A stationary lot is one in which all the items are simultaneously available for inspection. Its advantages are that the planning is easier, the various items can be easily identified and it is possible to have re-sampling and sequential sampling. However, to arrange all the items of the lot such that each item is accessible to the inspector to avoid bias is a difficult problem. In the case of moving lot, the various items flow past the point of inspection and as designed,
a few items are selected at a time from the moving batch. Sampling from moving lot is very convenient in the case of bulk materials like coal, grains, etc.
An item-lot consists of an aggregate of discrete items, or an aggregate of items of continuous or bulk materials which have been rendered discrete in the form of specimens or increments. A bulk lot is presented in the form of continuous or bulk material. As stated above if the continuous or bulk material is presented in the form of increments, (e.g., continuous length of cloth presented in the form of pieces of 1 metre, or oil tinned into containers of 1 kg capacity) then it will be treated as item lot.
A homogeneous lot is one which comes out from a process under statistical control. In order to have high efficiency of sampling it is desirable to maintain high degree of homogeneity of a lot, and for this purpose the lot should be confined to the items or products originating from essentially similar conditions. Under the conditions where a lot is formed by combining various sub-lots coming from different sources then, as far possible, the identity of the sub-lots should be preserved so that efficient stratification can be achieved.
When the lot size is very big, then for considerations of economy in inspection or efficiency of sampling, it may be considered desirable to divide the lot into sub-lots. Even if the sub-lot is very bulky then the division into sub-lots may be carried on two or more stages as well. An example of such a case will be to find the quality of coal coming from a mine. Say the coal is coming in the truck-load by the rails. First it may be decided to sample the rails, i.e. sampling be done once in a week. After a particular train is selected, then a small number of wagons are selected and further from each wagon equal quality samples are taken and inference drawn. It may be stressed here that inference will finally be made about the lot as a whole and not about each sub-lot. Such a method of sampling is also known as sampling in stages.
(iii) In the formation of lot, the decision about the size of the lot is also very important item. As a general rule the lot size should be as large as possible keeping two things in view, viz.,
(a) a reasonable degree of homogeneity should be maintained, i.e., the items in the lot should not differ widely in quality, and
(b) we should be able to arrange the various items of the lot such that the inspector will have easy access to all the items for selection of a sample. This calls for proper storage and handling facilities.
The advantage in having a bigger lot size is that, for any given degree of efficiency of sampling and for the same degree of homogeneity in the lot, the sample size will not increase as rapidly as the lot size and will not increase after a certain size for a lot. In other words, having a bigger lot size means the inspection cost is low.
On the other hand, if a large lot is rejected, then 100% inspection means cost of inspection will increase enormously and therefore a suitable compromise is essential in deciding the lot size.
As it is very important condition in the formation of a lot that the items must be of a single type, grade, class, size etc., produced under relatively uniform conditions of a manufacture ; it is proposed that the items for a lot be taken from a single batch of raw material or from component parts obtained from a single source, or manufactured by a single production method, or obtained from a single production line with the same dies and fixtures, or manufactured during single production shift, or produced from one setting of the machine and so on.
(iv) Determination of sample size : It may be again stressed that the method of determining the sample size for the purpose of assessing the lot quality is different than the method of
determining the sample size for the purpose of lot acceptance. Both these methods are discussed in details later.
Here we are broadly outlining the factors which require due consideration in deciding the size of the sample :
(a) We should be clear about the extent of error (risk element) that we can tolerate due to sampling.
(6) Degree of homogeneity in the lot.
(c) Lot size: As already stated a smaller lot size means that the sample size will be bigger in percentage (relatively), whereas the percentage of items in a sample for a bigger lot will be comparatively very less.
(d) The inspection cost should be minimum.
(v) Determination of item size or sample-unit size : This problem arises in case of bulk or continuous materials. (It is obvious that items in the sample can be either in the discrete form, i.e. single integral unit of product which can’t be further sub-divided, or in the continuous or bulk materials form). Under such situation, item is defined as a specimen of specified length, or as a specimen of a specified area, or as a relatively small portion of specified weight or volume of the bulk or the increment.
The determination of size of the item in such cases is very important factor in sampling techniques.
In the case of bulk-lots, usually larger the size (area, volume or weight) of the item, greater would be sampling efficiency, but beyond a certain size for the item the rate of gain in the sampling efficiency may be negligible. Besides from practical considerations, the large size of the increment for bulk products like iron ore, coal etc., may also pose problems like limitations of manual sampling, introduction or errors due to crushing, etc.
However, if sampling efficiency is the only criterion for determining the item size, then that size, beyond which the rate of gain in efficiency would be very small, may be taken as the appropriate item size.
For determining the item size following this principle, statistically designed experiments should be conducted covering different sizes for the item with respect to the item quality characteristics of interest. Corresponding to each size considered, from the values of the item quality, a measure of variability in item quality should be calculated. These values plotted against different sizes for the item would give a curve. In general, this curve would slope downwards in the direction of increase in the item size and would be more or less flat after a certain point. The size corresponding to this point would be an appropriate item size.
In an investigation conducted on coal of sizes 38 to 60 mm, seven series of 35 increments (to be considered as items) each were collected. The increments in each series were of approximately equal size which were analysed for ash content, individually. The average size of the increments in each series and the corresponding measure of variability (co-efficient of variation, v) of ash content were as follows :
| Series | Average size of increments (weight) | Co-efficient of variation v of ash content |
| 1 | 94 g | 61.1 |
| 2 | 345 g | 50.7 |
| CO | 978 g | 41 |
| 4 | 1.7 kg | 33.5 |
| 5 | 2.4 kg | 29 |
| 6 | 3.6 kg | 23.4 |
| 7 | 3.9 kg | 22 |
The co-efficient of variation of ash content between the increments has been plotted against the average size of the increments in Fig. 19.27.
On the basis of this investigation about 3.5 kg could be taken as a suitable size of the increment as increments of larger size do not decrease the co-efficient of variation appreciably.
(vi) General conditions for gross sample, i.e. mixture of all items (increments) selected from single bulk-lot or a sub-lot.
In order to gather maximum information regarding item quality in
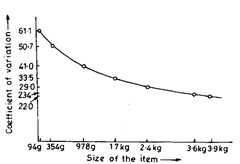
Fig. 19.27. Determination of Item Size.
case of bulk material, it is advisable to keep each increment in a separate container so that its identity is maintained. However, in cases, where the inspection cost of bulk material is high ; the increments selected in accordance with the principles of the sample selection may be mixed up thoroughly to form a gross sample (it may be noted that the samples being of smaller size, compared to the whole bulk, can be easily mixed up thoroughly so that a small sample taken out of the gross sample will be representative of the full sample ; this process is sometimes known as reduction) and inspection done on it. This method provides an estimate of the average quality as efficiently as the one based on inspection of each individual increment within the gross sample. However, it may be appreciated that a single gross sample is not sufficient to give any information about the variability in the lot, or to provide a measure of the sampling error involved and of the reliability of the assessment made of the average quality level.
