ABSTRACT
Substrate influence is a common problem when using instrumented indentation (also known as nano-indentation) to evaluate the elastic modulus of thin films. Many have proposed models in order to be able to extract the film modulus (Ef) from the measured substrate-affected modulus, assuming that the film thickness (t) and substrate modulus (Es) are known. Existing analytic models work well if the film is more compliant than the substrate. However, no analytic model accurately predicts response when the modulus of the film is more than double the modulus of the substrate. In this work, a new analytic model is reviewed. Using finite-element analysis, this new model is shown to be able to accurately determine film modulus (Ef) over the domain 0.1 < E/Es < 10. Finally, the new model is employed to determine the Young’s modulus of low-k and silicon carbide films on silicon.
Introduction
The problem of determining intrinsic film properties from indentation data that are influenced by both film and substrate is an old one. If the film is thick enough to be treated as a bulk material, then the analysis of Oliver and Pharr (1992) is typically used [3]. When the film is so thin that indentation results at all practical depths are substantially affected by the substrate, the influence of the substrate must be accurately modeled in order to extract the properties of the film alone. Since 1986, many such models have been proposed [2, 4-13].
In 1992, Gao, Chiu, and Lee proposed a simple approximate model for substrate influence. They derived two functions, I0 and Ii, to govern the transition in elastic properties from film to substrate[2]. Beginning in 1999, Song and his colleagues took an alternate solution path which was originally suggested by Gao et al. but not followed [8-10]. This alternate path yielded a simpler model which is called the "Song-Pharr model" in the literature. The Song-Pharr model predicts substrate effect reasonably well when the film is more compliant than the substrate. In 2011, Hay and Crawford developed a modified version of the Song-Pharr model which better handles the case of stiff films on compliant substrates[1]. In this article, the Hay-Crawford model will be explained and applied to material systems of broad interest: low-k and silicon-carbide films on silicon.
The Hay-Crawford model is a development of the Song-Pharr model, which in turn, draws from the Gao model. The Hay-Crawford model requires these inputs:
• ja, the apparent (or substrate-affected) shear modulus of the film,
• Vf, the Poisson’s ratio of the film,
• t, the film thickness,
• js, the shear modulus of the substrate, and
• Vs, the Poisson’s ratio of the substrate.
The output of the model is U, which is the substrate-independent shear modulus of the film. (Throughout this work, the subscript "f" means "of the film," the subscript "a" means "apparent," and the subscript "s" means "substrate".)
All of the inputs to the Hay-Crawford model are readily available from a regular indentation test. The apparent shear modulus, U, is simply that which is calculated by the Oliver-Pharr method [3, 14, 15]. It should be noted that most commercial indentation systems output Young’s modulus, E.
Although the model requires Poisson’s ratio for both film and substrate, the results are actually very insensitive to these parameters, so educated guesses are fine if definitive measurements are unavailable. (For glasses and ceramics, use v= 0.2; for metals, use v= 0.3; for polymers, use v= 0.4.)
Theory
The Hay-Crawford model is based on the supposition that, subject to an indentation force, the film has the potential to act both in series and in parallel with the substrate as illustrated schematically in Figure 1. It is rather intuitive that the film may act in series with the substrate. However, as the film becomes more and more stiff relative to the substrate, it begins to act more and more like a spring in parallel with the substrate. There are several ways to consider the sense of this configuration. First, as the film becomes stiff, it dominates the response, and this is what happens with parallel springs—the stiffer spring dominates. Second, as the film becomes thin and stiff, the deformation in the top layer of the substrate approaches that of the film. If two springs of different stiffness experience the same deformation subject to the same force, then they should be modeled as parallel. Finally, if the film provides significant lateral support, then it effectively acts on the indenter like the leaf springs which support the indenter column, and these leaf springs are well modeled by a parallel spring.
Fig. 1 Schematic of the proposed model allowing the film to act in series and in parallel with the substrate; the constant![]() relates bulk modulus to stiffness; it cancels out of the expression derived from this model (Eq. 2)[1].
relates bulk modulus to stiffness; it cancels out of the expression derived from this model (Eq. 2)[1].
Springs in parallel are treated together by adding their stiffnesses. Thus, the Hay-Crawford model relates the apparent shear modulus to that of the film and the substrate through:
Eq. 2 contains two factors for moderating the film influence: an empirical constant F and a weighting function I0. A constant value of F = 0.0626 has been determined by finite-element analysis [1]. This single value for F holds for any film-substrate system. The weighting function, I0 is that of Gao et al [2]. The function I0 is plotted in Figure 2 and given by
Eq. 2 gives us the right behavior in the limits of![]()
![]() When Io is close to 1, as it is at shallow penetration depths, the apparent modulus approaches that of the film. As I0 approaches 0, as it does at large depths, the apparent modulus depends on both the film and the substrate through the first term on the right-hand side of Eq. 2. In the case of a compliant film on a rigid substrate (Uf << us), Eq. 2 reduces to a model for two springs in parallel, which in fact, is the Song-Pharr model [8-10]. Finally, when the film modulus is very large, the apparent compliance goes to zero for all values of I0, as it should.
When Io is close to 1, as it is at shallow penetration depths, the apparent modulus approaches that of the film. As I0 approaches 0, as it does at large depths, the apparent modulus depends on both the film and the substrate through the first term on the right-hand side of Eq. 2. In the case of a compliant film on a rigid substrate (Uf << us), Eq. 2 reduces to a model for two springs in parallel, which in fact, is the Song-Pharr model [8-10]. Finally, when the film modulus is very large, the apparent compliance goes to zero for all values of I0, as it should.
Fig. 2 Gao’s weighting functions I0 and Ii which govern the film-to-substrate transition for shear modulus and Poisson’s ratio, respectively [1, 2]
The shear modulus of the film is calculated from the apparent value by solving Eq. 2 for u:
Finally, the Young’s modulus of the film is calculated from the shear modulus and Poisson’s ratio as
Calculation of U from standard indentation results for use in Eq. 2 requires a value for Poisson’s ratio. The weighting function I0 also utilizes Poisson’s ratio. But what value should be used—that of the film or that of the substrate? To be sure, this problem is of second order, but Gao et al. also provided a weighting function, I1, for handling the transition in Poisson’s ratio. Gao’s function I1 is also plotted in Figure 2 and given by [2]
Using Gao’s weight function, the apparent Poisson’s ratio, va, is calculated as [8-10]
Eq. 7 provides the value for Poisson’s ratio used in the calculation of![]() It should be noted that if film and substrate have the same Poisson’s ratio (that is, if
It should be noted that if film and substrate have the same Poisson’s ratio (that is, if![]() ), then Eq. 7 reduces to
), then Eq. 7 reduces to![]()
Finite-element analysis
Finite-element analysis (FEA) is essential to the development and verification of analytic contact models, because FEA idealizes experiment. In a finite-element model, the film thickness, film properties, and substrate properties are all well known, because they are required inputs. Also, there is little ambiguity about the true contact area under load, because it is determined from the last node(s) in contact. So before turning to experimentation, the worth of an analytic model is first assessed by means of FEA. For example, an elastic finite-element model may be constructed with a film of thickness t on a substrate, with the input properties being the Young’s modulus and Poisson’s ratio of the film (Ef, Vf), and the Young’s modulus and Poisson’s ratio of the substrate (Es, Vs). Then, indentation into the material is simulated, and the simulated force-displacement data are analyzed in order to achieve a value for the Young’s modulus of the film, i.e. Ef-out. What is the difference between this output value and the value that was used as an input to the finite-element model? FEA allows this question to be answered systematically over the domain of situations that might be encountered experimentally: thick films, thin films, stiff films on compliant substrates, compliant films on stiff substrates, etc. If an analytic model applied to simulated data fails to return the input properties with sufficient accuracy, it should not be expected to work well when applied to experimental data.
Some simulation inputs were fixed, and some were systematically varied in order to investigate the domain of interest. Table 1 summarizes the 30 finite-element simulations performed in this work. The film thickness was set to 500nm for all simulations; indentation depth was varied in order to investigate the domain of 4% < h/t < 40%. All indented materials, both film and substrate, were assigned a Poisson’s ratio ( v) of 0.25 and a linear-elastic stress-strain curve. (Thus, neither the effect of plasticity nor of transition in Poisson’s ratio was investigated by FEA.) The Young’s modulus of the film was fixed at 10GPa. To achieve the desired variation in E/Es, the substrate modulus was varied between 100GPa (E/Es = 0.1) and 1GPa (E/Es = 10). The modulus ratios are the same whether expressed in terms of Young’s modulus or shear modulus, i.e. jj/j = Ef/Es.
For all simulations, the indenter was a cone having an included angle of 140.6o and an apical radius of 50nm. This shape is the two-dimensional analogue of the common Berkovich indenter. The indenter was defined to be a linear-elastic material having the properties of diamond: E = 1140GPa and V = 0.07.
Table 1 Summary of finite-element simulations, showing values for inputs that were varied. For all simulations, the indenter was a 2-dimensional version of a Berkovich diamond. For the sample, t = 500nm, Ef = 10GPa, and Vf = Vs = 0.25 [1].
|
Simulation |
Es, GPa |
|
Maximum indenter displacement (h), |
nm |
|||||||
|
1-10 |
100 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
166 |
174 |
|
11-20 |
10 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
21-30 |
1 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
The purpose of simulations 11-20 was to verify the finite-element model. For these ten simulations, the finite-element model had the mesh of a film-substrate system, but with film and substrate having the same modulus (i.e. Ef = Es =10 GPa), and so behaving as a bulk sample. Application of standard analysis to the simulated data from runs 11-20 (for which E/Es = 1) yielded an output modulus that differed from the input value by no more than 1%.
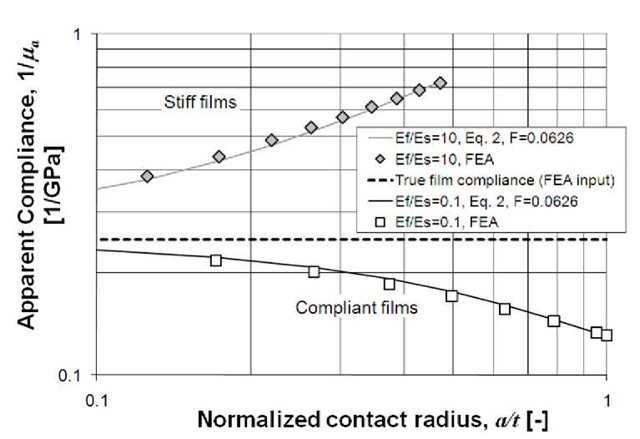
Figure 3 shows the finite-element results for simulations 1-10 and 21-30 in terms of apparent compliance (1/j) versus normalized contact radius (a/t). Indeed, the finite-element results for apparent compliance are well modeled by the Hay-Crawford model (Eq. 2). In this plot, the dashed centerline marks the true modulus for the film—the value that was used as an input to the finite-element simulations.
Fig. 3 Comparison between Hay-Crawford model and finite-element results for the film/substrate systems having the most severe modulus mismatch
FEA results are shown as discrete data points; each data point represents a single simulation of pressing the indenter into the film to a prescribe depth and withdrawing it, then analyzing the simulated force-displacement data by the Oliver-Pharr [3] method to achieve apparent compliance. FEA results for stiff films on compliant substrates (E/Es = 10) fall above true film compliance. For these simulations, the apparent compliance increases with increasing penetration depth due to the increasing influence of the compliant substrate. The FEA results for compliant films on stiff substrates (E/Es = 0.1) fall below the true film compliance. For these simulations, the apparent compliance decreases with increasing penetration depth due to the increasing influence of the stiff substrate. The solid curves in this plot show the apparent compliance as predicted by the Hay-Crawford model (Eq. 2) under the same circumstances. The excellent agreement between Eq. 2 and FEA justifies using Eq. 2 to interpret experimental results.
Experimental Procedure
Samples
Four samples were tested:
• C1: 249nm low-k on Si
• C2: 488nm low- k on Si
• S1: 150nm silicon-carbide (SiC) on Si
• S2: 300nm silicon-carbide (SiC) on Si.
Film materials were typical for their respective applications, but these samples were chosen to illustrate the utility of the Hay-Crawford model. For the "C" samples, the film was expected to be substantially more compliant than the substrate; for the "S" samples, the film was expected to be stiffer than the substrate. Samples within a pair were comprised of the same film material, with the only difference being thickness. For all samples, the elastic properties of the silicon substrate were assumed to be Es=170GPa and vs = 0.2GPa.
Equipment and Procedure
All samples were tested with an Agilent G200 NanoIndenter (Chandler, AZ), utilizing continuous stiffness measurement (CSM) and a DCM II head fitted with a Berkovich indenter. Results were achieved using the NanoSuite test method "G-Series DCM CSM for Thin Films," which includes an implementation of the Hay-Crawford model. At least 8 tests were performed on each sample. Loading was controlled such that the loading rate divided by the load (P ‘/P) remained constant at 0.05/sec. The excitation frequency was 75Hz, and the excitation amplitude was controlled such that the displacement amplitude remained constant at 1nm.
Results and Discussion
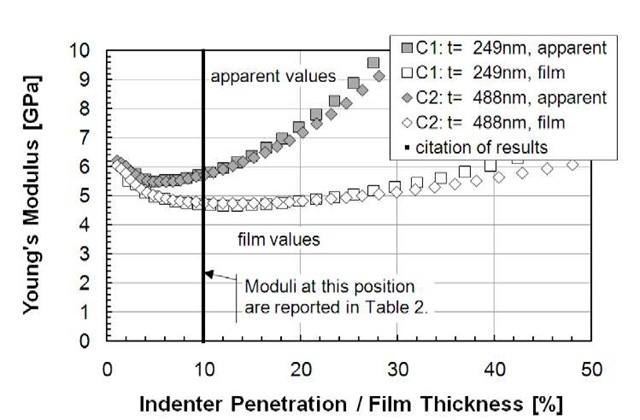
Figure 4 shows Young’s moduli for the two low-k samples as a function of normalized indenter penetration. Each trace represents the average of all tests done on that sample. The gray symbols are the measurements obtained by applying the Oliver-Pharr analysis to continuous-stiffness data [3, 15]. As a function of normalized penetration, the apparent moduli (gray symbols) first decrease, then increase due to the increasing influence of the silicon substrate. It is difficult to know whether the initial decrease is the manifestation of a real variation in properties (stiffer surface layer) or an experimental artifact (high strain rate at contact). Either way, properties measured in this regime are not representative of the bulk of the film. The open symbols in Figure 4 have the same underlying physical measurements as the gray symbols, but the open symbols show the results of applying Eqs. 2-7 to obtain the substrate-independent moduli of the films.
Fig. 4 Apparent modulus and film modulus as a function of normalized indenter penetration for low-K samples
When the indenter penetration exceeds 20% of the film thickness, the open traces also begin to rise. This is "substrate effect" only in an indirect sense: the hard substrate is causing the film material to "pile-up" around the face of the indenter. The analysis for determining contact area does not account for such deformation, and so calculated contact areas are too small, thus making calculated moduli too large. (This effect is also present in the gray traces, but it is overwhelmed by true substrate effect.)
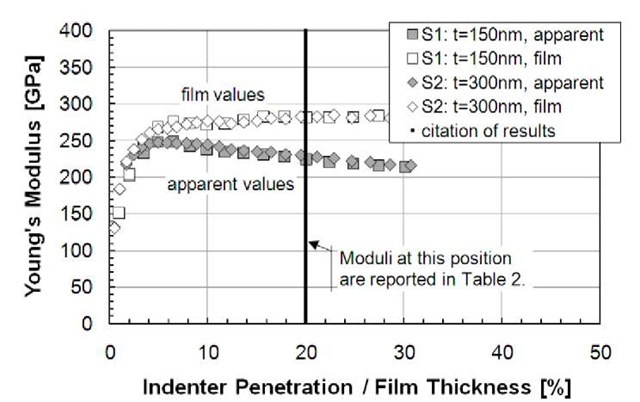
Figure 5 shows Young’s moduli for the two SiC samples as a function of normalized indenter penetration. Again, each trace represents the average of all tests done on that sample. The gray symbols show the results of applying the Oliver-Pharr analysis to continuous stiffness data; the open symbols show the results of additionally using Eqs. 2-7 to calculation the substrate-independent moduli of the films. As a function of penetration depth, the apparent moduli first increase, then decrease due to the increasing influence of the silicon substrate. Again, it is difficult to know whether the observed change in the first few nanometers of contact is due to a real change in properties or experimental artifact. Experimental issues which could cause this gradual increase include surface roughness and errant area function. (The "area function" is a polynomial which relates distance from the apex of the diamond to cross-sectional area; it is used to calculate contact areas.)
Fig. 5 Apparent modulus and film modulus as a function of normalized indenter penetration for SiC samples
After the initial increase, however, the film moduli (open trace) remain constant with increasing penetration depth. Although this doesn’t absolutely prove the validity of the Hay-Crawford model, it is certainly reassuring. For these samples, the degree of modulus mismatch is not as extreme (as compared to the "C" samples). Thus, we choose to report report properties at 20% of film thickness, rather than at 10%.
Young’s moduli for all four films are summarized in Table 2. Use of the Hay-Crawford model substantially changed the reported moduli for the films. For the low-k samples, the film modulus was about 17% lower than the apparent modulus at the same normalized displacement; for the Si-C samples, the film modulus was about 25% higher than the apparent modulus.
Table 2 Summary of experimental results [1]
|
Sample ID |
Description |
t nm |
 |
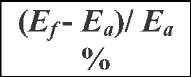 |
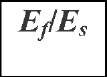 |
|
C1 |
low-k on Si |
249 |
4.69±0.146 |
-18.4 |
0.028 |
|
C2 |
low-k on Si |
488 |
4.77±0.074 |
-16.5 |
0.028 |
|
S1 |
SiC on Si |
150 |
284±9.50 |
26.0 |
1.67 |
|
S2 |
SiC on Si |
300 |
284±15.4 |
23.5 |
1.67 |
Conclusions
The Hay-Crawford thin-film model (Eq. 2) has been shown to accurately relate the apparent modulus obtained from an instrumented indentation experiment to the moduli of film and substrate, thus allowing the extraction of film modulus if substrate modulus and film thickness are known. The model works well for both compliant films on stiff substrates and vice versa. Application of this model to low-k and SiC films revealed substantial differences between apparent and film moduli.
![Schematic of the proposed model allowing the film to act in series and in parallel with the substrate; the constantrelates bulk modulus to stiffness; it cancels out of the expression derived from this model (Eq. 2)[1]. Schematic of the proposed model allowing the film to act in series and in parallel with the substrate; the constantrelates bulk modulus to stiffness; it cancels out of the expression derived from this model (Eq. 2)[1].](http://what-when-how.com/wp-content/uploads/2011/07/tmp1660_thumb_thumb.jpg)
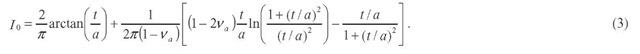
![Gao's weighting functions I0 and Ii which govern the film-to-substrate transition for shear modulus and Poisson's ratio, respectively [1, 2] Gao's weighting functions I0 and Ii which govern the film-to-substrate transition for shear modulus and Poisson's ratio, respectively [1, 2]](http://what-when-how.com/wp-content/uploads/2011/07/tmp1670_thumb_thumb.jpg)