Basic Principles of Two-Dimensional Graphics (Introduction to Computer Graphics Using Java 2D and 3D) Part 5

Movements via Transformations in Java 2D

This section explains how to implement the simple example of the moving clock of the previous section in Java 2D. Within the topic, only the most essential parts of the source code are shown. The full source code for this example can be found in the class NonSynchronizedClock.java.

In order to specify the location of the objects and the transformations in standard coordinates with the y-axis pointing upwards, the transformation yUp introduced on page 31 is applied to the Graphics2D object.

Initially, the frame of the clock will be centred in the origin of the coordinate system. It is represented by the object clockFrame of the class Rectangle2D. The single hand of the clock named clockHand is also generated as an object from the class Rectangle2D. Its initial position is chosen in such a way that it starts in the origin of the coordinate system and points upwards with the y-axis as its centre axis.

The transformations TcloCk,step, Thand,step, Tclock,accTrans, hand, accRotation and Thand,acc as described above are represented by the objects singleTranslation, singleRotation, accumulatedTranslation, accumulatedRotation and handTransform, respectively, all belonging to the class AffineTransform.

The transformation singleTranslation is defined as a translation by the vector (2, 1)T, whereas singleRotation is a clockwise rotation by an angle of 6°. Both transformations remain unchanged, while the program is running.

The transformation accumulatedRotation is initialised as the identity. The transformation accumulatedTranslation could also be initialised as the identity. But this would lead to the effect that the clock starts its movement centred in the lower left corner of the window, so that in the beginning only the upper left quarter of the clock would be visible. Therefore, a suitable translation is chosen for the initialisation of accumulatedTranslation ensuring that the clock is fully visible, when the animation is started.

A loop is used to compute the stepwise changing positions of the clock and the hand. In this loop, the transformations accumulatedTranslation, accumulatedRotation and handTransform are updated according to the equations specified on page 33. This is realised by the following lines of code:

The first line corresponds to the first equation, the second line to the second equation and the last two lines implement the last equation.

After the transformations have been updated in this way, the old image must be deleted and afterwards the frame of the clock and its hand have to be drawn again. Before these objects are drawn, the corresponding transformations are applied to them making sure that they are positioned at their updated locations.

The initial objects clockFrame and clockHand for the frame of the clock and for its hand, respectively, are not changed in the loop. Only the transformations applied to them change and the updated transformations are used to generate new objects of the class Shape that are drawn in each step.

The implementation proposed here has various disadvantages. Since all computations for the animation are carried within the paint method, this might lead to flickering and it might also be difficult to stop the animation since the paint method has a high priority in order to avoid showing half-ready images. For MAC computers the animation might not work at all since all computations in the paint method will be carried out completely, before anything is drawn on the screen. The program NonSynchronizedClock.java also uses a very primitive sustain method for the intermediate time between two frames. This method implements active waiting which should be avoided in programming. The double buffering technique introduced in Sect. 4.2 offers a much better solution than the one provided here which was only presented for reasons of simplicity.

Interpolators for Continuous Changes

The previous two sections have demonstrated how moving objects can be modelled on the basis of suitable transformations. Single stepwise transformations describe the changes of the objects from one image frame to the next one. The composition of these stepwise transformations determines the complete movement of an object.

But there are also other ways to model movements or changes of objects in animated graphics. An alternative approach is based on the two descriptions of the initial state of the considered object and of its desired final state. The aim is then to find an animation that shows a continuous transition of the object from the initial to its final state. The movement of an object along a line can either be modelled by small stepwise translations to be carried out between two image frames as in the previous two sections or by simply specifying the initial and the end position of the object and then carrying out interpolations between these two positions.

Fig. 2.21 Changing one ellipse to another by convex combinations of transformations

In the example of the clock from the previous two sections, one would not define the transformation Tclock, step = T (2,1) to be applied repeatedly to the clock in a sequence of, for instance, 100 images. Instead, it would be sufficient to specify the initial and the end position of the object, say p0 = (0, 0)T and p1 = (200,100)T.

The points p on the connecting line between the points p0 and p1 are simply the convex combinations of these two points given by

a = 0 yields the initial point p0, a = 1 leads to the end point p1 and a = 0.5 defines the point in the middle between p0 and p1.

This principle of convex combinations can be applied not only to points or vectors, but also to matrices. Later on, in Sect. 4.7 the principle of convex combinations will also be applied to colours to generate continuous changes from one colour to another.

In order to understand how convex combinations applied to matrices can be used to generate animations, two affine transformations are considered, given by the matrices M0 and M1 in homogeneous coordinates. The convex combination Ma of the two matrices is defined as

Note that Ma is again a matrix describing an affine transformation in homogeneous coordinates. In the simplest case, the two matrices encode translations mapping an object to its initial and its desired final position. The matrices Ma correspond to intermediate translations. Ma places the object on the points on the line connecting the initial and the end position. For α = 0, Ma maps the object to its initial position and for a = 1 to its final position.

However, convex combinations are not restricted to translations. In principle, the matrices M0 and M1 can represent any two affine transformations that do not even have to belong to the same type of transformation. One could be a rotation, the other a scaling combined with a shearing.

In this way, a continuous transformation can be implemented between two objects obtained from the same object by applying two different transformations. Figure 2.21 illustrates this process for two ellipses that were both generated from the same basic object—also an ellipse—by applying different scalings and transformations. The ellipse in the upper left corner is obtained from the basic ellipse by applying the first transformation, whereas the second transformation yields the ellipse in the lower right corner. Applying convex combinations of these two transformations to the basic ellipse leads to the ellipses in between.

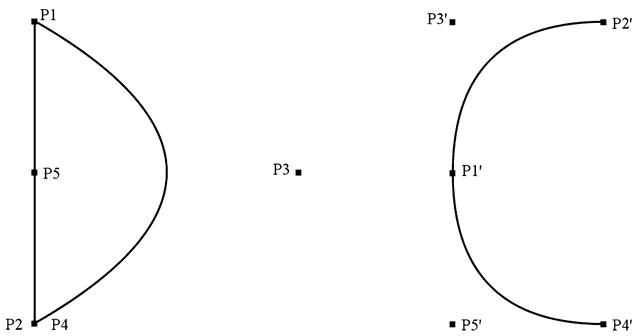
Fig. 2.22 Two letters each defined by five points and two quadratic curves

Another technique for continuous interpolation between two objects S and S’ assumes that both objects are determined by n points Pi = (x\,y\),…,Pn = (xn,yn) and P{ = (xj ,y[),...,P^ = (x'n ,y'n), respectively, and by lines or quadratic and cubic curves defined using these points. It is important that the lines or curves in both objects are determined by the corresponding points. This means, if a quadratic curve defined by the points P1, P3 and P8 is part of object S, then the corresponding quadratic curve defined by the points Pj, P^ and P^ must be part of object S'.

Figure 2.22 shows two simple objects in the form of the two letters D and C. For each of them five control points P 1,...,P5 and P1' ,...,P5', respectively, are specified. Both letters are described by two quadratic curves:

•    One curve uses the corresponding first and second point as endpoints and the third point as control point. In the case of the letter D the three points are P1, P2 and P3, respectively, for the letter C the corresponding points are P1', P2' and P3', respectively.

•    The other quadratic curve of each letter has the corresponding first and fourth point as endpoints and the corresponding fifth point as control point.

In order to continuously transform the two objects—in this case the letters D and C—into each other, convex combinations are applied again. Instead of having convex combinations of transformations as in the previous example of the ellipses, here convex combinations between pairs of corresponding points Pi and P' are considered.

Fig. 2 .23 Stepwise transformation of two letters into each other

For an intermediate image α e[0,1] the corresponding lines or curves are now (α) drawn on the basis of the points P( ). In the example of transforming the letter D into the letter C one would draw two quadratic curves, one defined by the points P^, P^ and P^, the other defined by the points P^, P^ and P^.

Figure 2.23 shows intermediate images obtained for the convex combinations with α = 0, 0.2, 0.4, 0.6, 0.8, 1 based on the points and the corresponding quadratic curves as illustrated in Fig. 2.22.

Further applications of interpolators in connection with colours and raster graphics will be introduced in Sect. 4.7.

Implementation of Interpolators in Java 2D

This sections explains in more detail how the two techniques for interpolators introduced in the previous section can be implemented in Java 2D.

The first example of a continuous transition from one ellipse to another as illustrated in Fig. 2.21 is realised in the class ConvexCombTransforms.java. In the first part of the program the basic ellipse elli and two affine transformations initialTransform and finalTransform are defined. The two transformations transform the basic ellipse into the initial ellipse in the beginning of the animation and the final ellipse at the end of the animation. In order to compute the convex combinations of the two transformations the corresponding matrices are required. They are obtained by applying the method getMatrix to initialTransform and finalTransform.

The coefficients of the two matrices are stored in the one-dimensional arrays initialMatrix and finalMatrix according to the representation of transformation matrices (2.1) on page 26. The intermediate images are generated in a loop where in each step a new convex combination of the two arrays is computed.

The arrays are treated in the same way as vectors5 so that their convex combination yields an array of the same length. The elements of this new array can again be interpreted as the coefficients of a transformation matrix in homogeneous coordinates. This transformation is then applied to the basic ellipse and in each step of the loop the resulting transformed ellipse is drawn.

The transformation of the letter D into the letter C is implemented in the class DToCMorphing.java. Figure 2.22 showing the initial state—the letter D—and the final state—the letter C—was generated by the classes SimpleLetterD.java and SimpleLetterC.java. For the transformation of the two letters into each other, two arrays are defined for each letter, one array for the x-coordinates of the control points and one array for the y-coordinates. Another two arrays are needed for the computation of the convex combinations of the control points. In each step of the loop the new convex combination is computed and the computed control points are used to draw the corresponding quadratic curves to generate the corresponding intermediate image.

Single or Double Precision

For longer animated graphics with moving objects a large number of transformations have to be applied successively. This means that a large number of matrix multiplications must be carried out. Although the roundoff error for a single matrix multiplication might be negligible, roundoff errors can accumulate over time and might lead to undesired effects. In most cases such roundoff errors will be noticeable in the graphics to be drawn since the numerical computations to be carried out in computer graphics are usually not critical from the numerical point of view. Inverting a matrix to reverse a transformation is an example for an exception where roundoff errors might have serious effects on the graphics, when the matrix is badly conditioned. But most of the calculations in computer graphics do not encounter such problems.

For illustration purposes the example of the second hand of a clock is considered. The hand is 100 units or pixels long. The tip of the hand is at the point (100, 0) in the beginning. The hand is rotated clockwise around the origin by 6° per second. This means that the transformation R(—6°) in terms of a rotation matrix is applied each time. After every full minute—after 60 multiplications of the rotations matrix by itself—the hand should return to its original position.

Table 2.2 shows the computed positions of the tip of the hand after various time intervals using double (double) and single (float) precision. In both cases the roundoff errors are negligible, especially when taking into account that drawing in raster graphics will require rounding to integer values in the end anyway. Even after eight hours demanding 28,800 matrix multiplications, single precision will still be sufficient to obtain the exact values in terms of raster graphics. This is only valid if the accumulated rotation is applied to the hand in its initial position or if the new position of the hand is stored in vector graphics, i.e., using floating point arithmetic, and every second a single rotation by 6° is applied to the updated position of the hand. If the coordinates of the hand are stored in raster graphics using only integer values and a single rotation by 6° is applied to the updated hand in pixel coordinates every second, already after one minute a wrong position of (95, —2) instead of (100, 0) is calculated.

Table 2.2 Effects of roundoff errors

Time	x	y
	double
1 minute	99.99999999999973	—4.8572257327350600E-14
2 minutes	99.99999999999939	—9.2981178312356860E-14
3 minutes	99.99999999999906	— 1.3739009929736312E-13
4 minutes	99.99999999999876	— 1.4571677198205180E-13
5 minutes	99.99999999999857	—2.2204460492503130E-13
6 minutes	99.99999999999829	—2.9143354396410360E-13
7 minutes	99.99999999999803	—3.1641356201816960E-13
8 minutes	99.99999999999771	—3.7331249203020890E-13
9 minutes	99.99999999999747	—4.2604808569990380E-13
10 minutes	99.99999999999715	—4.5657921887709560E-13
8 hours	99.99999999986587	—2.9524993561125257E-11

	float
1 minute	100.00008	— 1.1175871E-5
2 minutes	100.00020	—1.4901161E-5
3 minutes	100.00032	—1.8626451E-5
4 minutes	100.00044	— 1.1920929E-5
5 minutes	100.00056	—8.9406970E-6
6 minutes	100.00068	—3.1292439E-5
7 minutes	100.00085	—5.3644180E-5
8 minutes	100.00100	—7.2270630E-5
9 minutes	100.00108	—8.0466270E-5
10 minutes	100.00113	—8.4191560E-5
8 hours	100.00328	—1.9669533E-4

Although computations with double precision values are less error-prone, the accuracy of single precision is sufficient for most applications in computer graphics taking into account that raster graphics will require rounding numbers to integer values in the end, so that numerical errors less than 0.5 are invisible anyway.

Especially for three-dimensional scenes with complex objects a very large number of points is needed to define the objects. In this case the memory requirements very often have a higher priority and single precision is preferred over double precision in order to reduce the amount of memory needed for storing the objects.