Population ecology deals with questions related to the density or number of individuals of a species in a habitat or location. Insect population ecologists try to understand why population densities of some insects fluctuate dramatically, but others show little variation in density. They want to know why some species are rare, whereas others are common. They seek to understand the mixture of factors affecting mortality and fecundity that together determine the characteristic density of a species and whether the density will decline or increase. Applied population ecologists try to understand the conditions that allow densities of pest insects to reach damaging levels, and they seek to modify those conditions to keep the densities below those levels. To isolate the effects of particular variables from the multitude of factors influencing population growth and survival, population ecol-ogists apply a range of tools to understand population systems, including gathering data on density, fecundity, and mortality from natural populations, construction of mathematical models of population interactions, and experimental manipulation of populations in the field.
ESTIMATING INSECT ABUNDANCE
Research on the population ecology of an insect typically begins with the development of sampling techniques to determine the abundance of the insect in the habitat under study. When the habitat has definable boundaries, we can estimate the number of individuals in the population. More frequently, we estimate density or number of individuals per unit of habitat. Sampling methods vary tremendously with habitat type. Specialized sampling techniques have been developed for insects that live in the soil, in the air, on foliage, and on vertebrate hosts. A large scientific literature exists on the methods developed for each of these habitats.
One can make several general distinctions about different methods of sampling insects. One of these is to distinguish between absolute and relative measures of density. Absolute measures quantify numbers per unit area or volume of habitat. Examples are numbers of grasshoppers per square meter in quadrat samples or numbers of Collembola per cubic centimeter of soil. Relative measures express numbers per sample unit, such as numbers of insects captured in a sweep-net sample or numbers of male moths captured in pheromone-baited traps. Relative measures may or may not reflect absolute density. They are frequently much easier to obtain than absolute measures, but they may be influenced by many factors (e.g., air temperature) that affect the activity of the insect and its likelihood of being captured. Consequently, much research is needed to be sure that relative measures give an accurate indication of differences in absolute population density. In addition, there are population indices, which are indirect measures of density, such as measures of defoliation.
Another general characteristic of sample methods is that some, such as sticky traps or pheromone-baited traps, obtain data continuously over an extended interval of time, whereas others obtain an essentially instantaneous “snapshot” of a population at a particular moment. Examples of the latter include sweep-net samples, quadrat samples, and insecticide knockdown samples. Such instantaneous samples are susceptible to the effects of time of day or weather conditions at the time of sampling, which in turn may influence the number captured. Continuous samples may also be influenced by weather conditions but, because capturing occurs over an extended interval, these effects are averaged over a range of such conditions.
Any investigator planning a sampling program must think carefully about how the samples will be selected. Consultations with statisticians with expertise in experimental design prior to collection of data is always wise, as is preliminary sampling or pilot testing to estimate the expected amount of sample variability. Most sampling schemes may be classified as random, systematic, or stratified random designs. In random sampling, the sample units are chosen or placed at randomly selected locations in the sample area. Random selection is typically done by choosing coordinate points from a table or list of random numbers. In a systematic design, sample units are placed at regular intervals across the sample universe (e.g., every 20 m or every 10th plant). Systematic samples are frequently much easier to conduct, and they ensure that the samples are distributed evenly across the sample universe. However, systematic samples violate the requirement that samples be selected independently and at random from the sample universe, imposed by most statistical analyses. Whether violation of this requirement leads to erroneous conclusions in any particular system is usually debatable. A reasonable compromise between the two approaches is a stratified random or randomized block design in which the sample universe is divided into regularly spaced subunits or blocks and samples are selected at random from each block. Differences in density between subunits caused by edge effects or density gradients across the field can be detected with appropriate statistical analysis.
Mark-recapture techniques are sometimes used to estimate insect abundance. Individuals are marked with a permanent mark that does not significantly alter the behavior of the insect or affect its survival. Marked individuals are counted and released into a population. Subsequently, a sample of individuals is collected from the population and the proportion (m/n) of marked individuals in the sample is recorded. Nearly all mark-recapture methods rest on the basic assumption that m/n of the sample is an estimate of the proportion of marked individuals in the larger population M/N. If one assumes that M, the number of marked individuals in the population, is equal to the number released, then the population size N can be calculated directly: N = M(n/m). This calculation is known as the Lincoln index or Peterson estimate. As a rule, it cannot be assumed that M is equal to the number of marked individuals released because some of them will have died or emigrated in the interval between release and recapture. Several fairly elaborate techniques involving multiple rounds of mark and recapture have been developed to estimate M when it is unknown.
Applied ecologists frequently use sequential sampling to classify populations into density categories such as high (requiring treatment) or low (requiring no treatment). The basic idea is to minimize the cost of the sampling effort by collecting only the number of samples needed to make this decision with sufficient statistical reliability. Development of a sequential sampling scheme for a particular insect and crop or habitat requires research to define the population density that forms the dividing line between the high and low categories, a definition of the degree of allowable risk for making an incorrect classification, and an estimate of the degree of clumping or patchiness that typifies the species.
POPULATION GROWTH AND LIMITS TO GROWTH
A fundamental property of the population dynamics of all species is that the number or density of individuals will grow at an ever-increasing rate when conditions are favorable. The simplest example of such growth is illustrated by the replication of single-celled organisms.
If a bacterium divides every hour, a colony that began with one individual would grow to 2, 4, 8, 16, … 2t, where t is the number ofhours or replications. With insects, the rate of replication with each generation is potentially much faster. The house fly, Musca domestica, for example, has generation time of approximately 2 weeks and lays more than 200 eggs. If half those eggs were females and all survived to maturity, the population would increase by more than a hundred fold each generation. By the end of 1 year the population would have increased to more than 1052 individuals (a mass of flies much larger than the earth). Even if mortality were much higher (e.g., only 1 fly in 10 survived to maturity), the end result would be similar but would take longer to achieve. Mathematically, we refer to this process as geometric or exponential growth, and for insects that reproduce continuously, it is typically expressed with the following equation (Fig. 1 ):
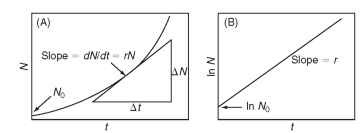
FIGURE 1 (A) Exponential growth of a population yields a straight line when density (N) is plotted vs. time (t), as in (B), on a logarithmic scale.
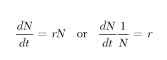
Here N is the population size or density, dN/dt is the growth rate (the change in density per unit time), and the constant r is the instantaneous per capita rate of increase. The parameter r equals instantaneous per capita birthrate minus the instantaneous per capita death rate. When the rates of birth and death are equal, r = 0 and the population ceases to grow. When the death rate exceeds the birthrate, r is negative and the population declines.
The notion of exponential population growth was first expressed in 1798 by T. R. Malthus, who observed that human populations increased exponentially, whereas food production increased in a linear fashion. As a result, Malthus predicted that mankind would be doomed forever to a life close to the edge of starvation. Malthus did not foresee the large increase in agricultural production that accompanied the Industrial Revolution, but he may yet prove to be correct. The ideas of Malthus were fundamental to the development of Darwin’s theory of evolution: all organisms must struggle to survive because all species produce more offspring than can survive.
It is obvious that no population can continue growing forever; sooner or later, it will reach a density above which individuals can no longer obtain the resources they need to survive. This density is known as the carrying capacity of the environment. For different species in different habitats, the carrying capacity will be determined by competition for particular resources. For desert plants, water is typically the limiting resource. For many animals, food supply determines the carrying capacity. As a population expands toward the carrying capacity, the rate of growth slows down. This process is typically represented by the following logistic equation (Fig. 2), which was first
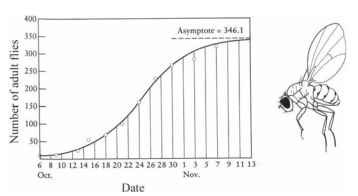
FIGURE 2 Logistic population growth model fit to data from laboratory colony of fruit flies.
applied to population growth by P. F Verhulst in 1838 and independently by R. Pearl and L. J. Reed in 1920:
![]()
Here K is the carrying capacity and r and N retain their earlier definitions. The first term (rN) represents exponential growth. The effect of the second term (rN2/K), often called environmental resistance, increases as N becomes large. As N approaches K, the rate of growth (dN/dt) approaches zero.
There are a number of assumptions inherent in the use of the logistic equation to represent population growth. The first is that unless disturbed, population density will approach the carrying capacity (K) and then remain stable about it. In actuality, most populations fluctuate in density, even populations kept in the laboratory under constant environmental conditions. Another assumption is that the shape of the curve is symmetrical above and below the midpoint. In fact, few population systems, even in the laboratory, follow the trajectory predicted by the logistic equation. Rather, the importance of the equation is its contribution to theoretical ecology. It captures the most basic processes of population dynamics: exponential growth and the effects of factors that limit growth. Variations of the logistic equation have been explored by many individuals; indeed, it is the foundation of a large body of work in theoretical population ecology. A. J. Lotka in 1925 and V Volterra in 1926 extended the logistic to describe both competition between species and predator-prey interactions. More recent applications include models of food webs and interactions between many species in a community.
REGULATION OF POPULATION DENSITY
Although no one doubts that competition for resources confers an upper limit on the growth of all populations, it seems clear that many populations of insects persist at densities far below any obvious carrying capacity. Furthermore, the densities of most species fluctuate within a fairly narrow range of values. For a population to remain at constant density, the birthrate must equal death rate. Each individual must on average replace itself with one surviving offspring. Indeed, for any species to persist over evolutionary time, the average birthrate must equal the average death rate, although these quantities may vary considerably from year to year. Organisms that experience high mortality compensate by producing lots of young. For this fundamental reason, most population ecologists believe that most populations are stabilized by factors that are called density dependent. Such factors influence birthrates or death rates in a way that varies systematically with density, such that populations converge to densities at which rates of birth and death are equal and the density is at equilibrium. Such factors act as a negative feedback system that is analogous to the regulation of room temperature by a thermostat. If densities rise above the equilibrium value, the death rate exceeds the birthrate and the population returns to equilibrium. If densities fall below the equilibrium value, the birthrate exceeds the death rate and the population increases.
Predators, pathogens, and parasitoids usually cause mortality to insects that is density dependent. The proportion or percentage of the population killed by these factors varies systematically with density. An increase in the proportion dying with increasing density is called positive density dependence; a decrease in the proportion dying with increasing density is termed negative or inverse density dependence. A mortality factor is density independent when the proportion killed varies in ways that are unrelated to population density. Many abiotic factors, such as mortality due to subfreezing temperatures, act in ways that are density independent. Although many insect population ecologists focus on sources of mortality, density-dependent changes in fecundity may either lead to changes in density or serve to stabilize densities. Certainly, competition for resources is a density-dependent process that will stabilize a population at the carrying capacity, if other factors do not intervene at lower densities.
For more than 50 years ecologists have debated whether population densities of most species are stabilized by such density-dependent factors. L. O. Howard and W. E. Fiske in 1911 were the first to articulate the idea that populations cannot persist long unless they contain at least one density-dependent factor that causes the average fecundity to balance the average mortality. Other early proponents of this idea in the 1950s were A. J. Nicholson and D. Lack. In contrast, H. G. Andrewartha and L. C. Birch argued in 1954 that most populations are not held at equilibrium density. Rather, densities merely fluctuate. In their view, most species avoid extinction because they comprise what we now call metapopulations, that is, a series of subpopulations that are linked by dispersal but whose densities fluctuate independently of one another. Extinction of subpopulations occurs quite frequently, but these are recolonized by individuals dispersing from other subpopula-tions, thereby allowing the species to persist indefinitely over the entire region. In recent years metapopulation dynamics has been explored by way of computer simulations, and these have revealed that in the absence of density dependence, such systems eventually go extinct.
The debate about the ubiquity of density-dependent processes has persisted despite the efforts of various ecologists to terminate the discussion either because it was bankrupt or because they deemed that prevalence of density dependence was too obvious to deny. Many ecologists have insisted that no conclusion can be made regarding the existence of density dependence in a population system unless its action can be demonstrated statistically in data collected from the populations. This has proved difficult to achieve. Until recently, adequate methods for detecting density dependence in population systems have been lacking, and earlier methods are now known to be statistically flawed. Several new methods were proposed in the decade following 1985, most of which involved a variety of computer-based resampling procedures, such as the bootstrap.
LIFE TABLES
Population ecologists typically summarize their collected mortality data in life tables, which express the proportion of the insects that survive to successive instars or life stages. The proportion dying in each instar or life stage can be partitioned into components caused by different agents of mortality. Techniques for quantifying mortality in this way were pioneered in the 1960s by R. F. Morris, who worked on spruce budworm, Choristoneura fumiferana, in Canada, and by G. C Varley and G. R. Gradwell in England, who studied the winter moth Operophtera brumata, a defoliator of oak trees in Europe. In 1960 Varley and Gradwell reported a 13-year study of winter moth survival to successive life stages at one site. They showed that pre-dation on pupae was density dependent and was responsible for maintaining a low-density equilibrium. Their studies illustrated the benefits of collecting data on density, fecundity, and mortality from the same populations over many generations. They developed a graphical procedure known as key-factor analysis to identify the life stages or causes of mortality most responsible for observed fluctuations in density. In the winter moth system, the key factor was overwintering mortality. Subsequent work offered analytic procedures for key-factor analysis, but others, such as E. Kuno and T. Royama, noted statistical shortcomings; as a result this procedure is rarely used.
Mortality from parasitoids and disease is typically measured by collecting a sample of hosts and dissecting them, or rearing them to determine the proportion that is parasitized or infected. This proportion, however, may or may not accurately reflect the total proportion of hosts attacked over a life stage or generation, since attack rates vary over time with the number of hosts available to attack and the number of adult parasitoids searching. In 1992 T. S. Bellows and colleagues reviewed the techniques that have been developed to convert proportion infected in samples to the summary values appropriate for life tables or for comparisons of parasitism between populations or treatments in a study.
PREDATORS, PATHOGENS, AND PARASITOIDS
Nearly all insect species are attacked by a suite of natural enemies and, as indicated earlier, these frequently act in a density-dependent manner that serves to maintain populations at densities well below the carrying capacity determined by resource limitation. Different natural enemies will attack different life stages. Predators are mobile organisms that feed on many prey. Predators of insects include many vertebrate and invertebrate species. Parasitoids are insects whose immature stages develop on or within a single host individual, usually killing it in the process. The majority of parasitoids belong to the order Hymenoptera or Diptera. Pathogens are microorganisms including viruses, bacteria, microsporidia, or fungi that infect a host and cause disease. Biological control focuses on the use of natural enemies to maintain the densities of pest insects at levels below that at which they cause damage.
Density-dependent predation or parasitism may arise from two different sources: the numerical response and the functional response. The numerical response is an increase in the density or number of predators or parasitoids in response to increasing prey density. The numerical response can arise from increased reproduction or survival of predator or parasitoid offspring induced by increases in prey availability, or it can arise from an aggregative response whereby predators and parasitoids are attracted to sites with high densities of prey.
The functional response is an increase in the number of prey taken per predator or parasitoid at increasing prey density. Important contributions to the understanding of the functional response were made by C. S. Holling beginning in 1959. In laboratory experiments, Holling presented individual predators with different numbers of prey. He showed that the number of prey consumed over a specified time interval increased with number of prey available, but at a decreasing rate toward an upper maximum (Fig. 3A). This effect is caused by an upper

FIGURE 3 Number of prey consumed per predator and the corresponding proportion consumed for type II (A, B) and type III (C, D) functional responses.
limit in the predator’s capacity for consumption and by the increasing proportion of time devoted to handling the large number of prey at the expense of time spent searching for prey. Above this limit, further increases in prey density will not cause higher consumption. The proportion of prey consumed plotted vs. prey density steadily declines (Fig. 3B), illustrating that the functional response is inherently inverse density dependent. Without a numerical response, predators and parasitoids are unlikely to stabilize a host population. Further work by Holling showed that under some important conditions, the functional response can lead to positive density-dependent predation. Whenever increases in prey density result in some change in the foraging behavior of the predator or parasitoid, such that foraging becomes more efficient or efforts are concentrated on the particular prey species, the number taken will accelerate with increasing host density (Fig. 3C) , and the proportion taken will increase (Fig. 3D) over the lowest range of prey densities. Holling termed this a type III functional response in contrast to type II, which is the continuous decline in proportion taken evident whenever there is no change in foraging behavior in response to changes in prey density (Fig. 3A and 3B). Holling demonstrated a type III response for shrews foraging for sawfly pupae. He envisioned type III responses to be characteristic of vertebrate predators, which have a relatively high capacity for learning and behavioral change. However, the type III functional response has subsequently been demonstrated in many insect predators and parasitoids.
Specialist or monophagous natural enemies are those that attack a single host species. Oligophagous natural enemies restrict their attacks to a closely related group of species. Generalist or polypha-gous natural enemies attack a wide range of host species. The distinction is important because generalists and specialists typically respond very differently to changes in host density. Specialists are most likely to exhibit a numerical response to changes in density of their prey because they depend on no other food sources and their seasonal development is closely linked with that of their prey. Generalists may exhibit little or no numerical response, because they depend on many types of prey and may shift from one prey to another, depending on which species are available. In fact, it is very common for many natural enemies, especially generalists, to exhibit inverse density dependence, wherein mortality declines as prey density increases. Such mortality cannot stabilize prey densities unless accompanied by a numerical response.
Many systems exhibit complex density dependence; for example, mortality from particular natural enemies may switch from positive to negative as host density increases. Thus, bird predation on forest-dwelling caterpillars that is density dependent at the lowest density may shift to inverse density dependence as the densities exceed the capacities of the predators to respond numerically and the functional response approaches the upper limit of prey consumption. Under such conditions, the prey densities may “escape” into an outbreak phase, which is characteristic of a few species. Outbreak populations are typically subject to a different suite of density-dependent factors, such as viral diseases and starvation, which become major sources of mortality only when densities are high. These factors can maintain populations at a high-density equilibrium, but more frequently they cause the collapse of populations back down to a low-density, endemic phase. In contrast, generalist predators, which might consume the majority of prey individuals at low density, are likely to consume a tiny fraction of the population at high density even though they are attacking the same or higher numbers of prey individuals at these high densities.
In 1976 T. R. E. Southwood and H. N. Comins proposed a “synoptic model” as a general feature of insects that occasionally go into an outbreak phase (Fig. 4) . Earlier expressions of this idea can be found in the writings of R. F. Morris and R. M. Campbell. The model is depicted by plotting R0, the net reproductive rate, against density. At intermediate densities in the ” natural enemy ravine, ” density-dependent mortality caused by natural enemies maintains the population at equilibrium (R0 = 1). The natural enemy ravine separates two “ridges,” one at high and one at low density, where mortality is lower and population densities increase. At very high density, other mortality factors such as starvation and disease cause the populations to collapse. At the extremes of low density, an “Allee effect” comes into play, caused primarily by the failure of individuals to find mates and reproduce. Populations in this range decline inexorably to extinction. Such low densities are infrequent in most natural populations, but they play a very important role in the establishment of invasive species.
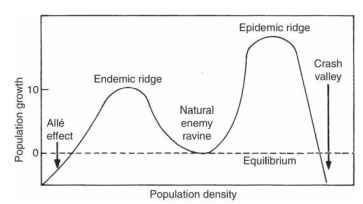
FIGURE 4 Synoptic model of complex density dependence.
Many incipient invasions go extinct without human intervention because not enough individuals were established to sustain the population (for a review, see Liebhold and Tobin, 2008). Similar processes constrain the introduction of natural enemies as biological controls of invasive species. The establishment of biological control agents will fail if insufficient numbers of them are released at each release site.
POPULATION MODELS
Theoretical ecologists have developed numerous population models to study the effects of natural enemies on their prey. Much insight has been gained from simple mathematical expressions that relate prey density to that of changes in density of specialist predators or parasitoids. One approach, pioneered by A. J. Lotka and V. Volterra in the 1920s, entailed a simple modification to the logistic equation by adding a term that represents prey consumption on densities of both host and predator:
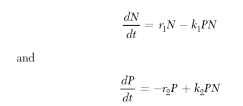
where N and P are the respective densities of host and predator, and the rates of population growth are given by dN/dt and dP/dt. In the first equation, the first term represents exponential growth of the host (r1N) in the absence of the predator, whereas in the second equation, the first term represents exponential decline in the predator (— ^P) in the absence of the host. The second term in each equation represents the effects of predation, which is determined by the encounter rate of host and predator and is proportional to PN. The constant k.1 is a measure of the ability of prey to escape predators, and &2 is a measure of the ability of predators to capture the prey. The model predicts a predator-prey oscillation (Fig. 5A). The changes in density of the predator or parasitoid lag behind those of its host. The highest rates of attack on the host occur at peak predator density, which is observed after the host population density has

FIGURE 5 (A) Predator-prey oscillation as predicted by a Lotka-Volterra model and (B) Host-parasitoid oscillation of the Azuki bean weevil in laboratory culture.
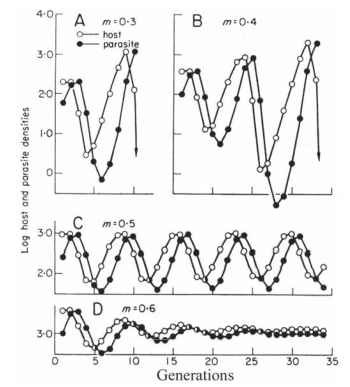
FIGURE 6 Stabilizing effects of mutual interference (m) between parasitoids on models of the Nicholson-Bailey type.
declined. Plotting percent mortality from the predator or parasitoid against host density would not reveal a consistent pattern of positive density dependence, even though the predator or parasitoid is clearly maintaining the host within a narrow range of density. This type of response is termed delayed density dependence. In the 1990s, P. Turchin and others developed new statistical methods based on time-series analysis for detecting delayed density dependence in annual census data. Laboratory studies of predator-prey interaction frequently show such predator-prey oscillations (Fig. 5B).
A different class of models appropriate for parasitoids and host populations with discrete generations was initiated by W. R. Thompson in 1924 and by A. J. Nicholson and V. A. Bailey in 1935. These models were difference equations, in contrast to the differential equations of the Lotka-Volterra type. The general form of the model expresses host or prey density N in generation t + 1 as follows:
![]()
Here A is the rate of increase per generation of the host in the absence of parasitism and f(Nt,Pt) is the proportion of hosts surviving parasitism in the preceding generation (t). Similarly, the number of parasitoids in the next generation Pt+\ is given by
![]()
where (1 — f(Nt,Pt) is the proportion of hosts attacked by parasitoids in generation t and c is the number of surviving parasite progeny produced per parasitized host. The notation f(Nt,Pt) stands for any function of Nt and Pt. Variations in the model involve incorporating different factors into f(Nt,Pt). The simplest version for f(Nt,Pt), proposed by Nicholson and Bailey, assumes that all hosts are equally likely to be attacked and that parasitoids search at ” random, ” such that the proportion of hosts that escape is given by the zero term of the Poisson distribution. This model predicts that hosts and parasi-toids will experience density oscillations of ever-increasing amplitude until both go extinct. Obviously, this does not occur routinely in nature.
In the 1960s, M. P. Hassell, R. M. May, and colleagues began an exploration, extending over several decades, of the various factors that would stabilize host-parasitoid interactions in models of this type. These factors included mutual interference of parasitoids, patchiness of hosts or parasitoid attacks, and variation in host susceptibility. For example, Fig. 6 illustrates how an increase in the magnitude of mutual interference between parasitoids will reduce parasitoid efficiency at high host density and thus stabilize the system. When mutual interference is low (Fig. 6A and 6B), or absent altogether (m = 0, as in the original Nicholson-Bailey version), the model oscillates with increasing amplitude and both host and para-sitoid go extinct. Other factors such as patchiness in parasite attacks have a similar effect.
The models described so far are relatively simple. They contain a small number of parameters or variables and leave out much of the known biology of the host and its natural enemies. Theoretical ecolo-gists focus on such models because they can be analyzed by a variety of mathematical tools and can be used to address questions of general ecological significance. They hope that the models capture the essential features of the systems they represent. Applied ecologists, in contrast, are often drawn to more complex models, because they wish to understand the complex interplay of environmental and biotic variables that account for the density fluctuations of particular species of interest. With modern computers, there is virtually no limit to the complexity that can be built into such models, but this does not mean that the resulting simulations will necessarily be useful or revealing. Many highly complex models constructed in the 1970s, when high-speed computers first became widely available, were abandoned because they failed to accurately predict the behavior of the systems they represented and were too complicated to understand. Many ecologists have advocated models of intermediate complexity. A good example of a sophisticated attempt to model a very simple population system with a family of models that vary in complexity is the 2005 work of W. M. Murdoch and colleagues on the Aphytis melinus/red scale system described below.
IMPACT OF GLOBAL CLIMATE CHANGE
In the last decade many insect ecologists have devoted their attention to the impact of global climate change on the abundance and spread of important insect species. There are many examples of insects expanding their range to higher latitudes and altitudes as climate warms. There have been several spectacular outbreaks of important forest insects. For example, the mountain pine beetle, Dendroctonus ponderosae, has vastly expanded its range in North America northward into British Columbia and caused unprecedented tree mortality. This insect has also moved into high altitude forests in the Rocky Mountain region where it has been killing pine tree species that have not been attacked before. These phenomena have been explained by sophisticated models of temperature dependent growth of mountain pine beetle devised by J. A. Logan and colleagues.
COMPETITION AND TROPHIC INTERACTIONS
When resources are limiting, intraspecific competition prevents growth of a population beyond the carrying capacity of the habitat. Interspecific competition occurs when two or more species compete for the same resource. Ecologists have long appreciated the importance of interspecific competition in shaping community structure and the interaction between species. Models of competition developed in the 1920s by Lotka and Volterra, analogous to those for predation, predicted that when two species compete for the same resource, under most conditions one species will win out and the other will go extinct. This phenomenon, which became known as competitive exclusion, was readily demonstrated in laboratory populations by G. F. Gause in the 1930s with microorganisms, and by T. Park and associates in the 1950s with flour beetles (Tribolium spp.). Coexistence occurs only when species do not overlap completely in their use of resources. To put it another way, two species cannot coexist if they occupy the same niche. Clear examples of competitive exclusion of insects in the field are harder to come by. Most examples involve introductions of insects to regions outside their native range. For example, the Argentine ant Linepithema humile has been introduced to many regions of the world and has outcompeted and excluded many native ant species. In California around 1900, biological control introductions of Aphytis parasitoids of California red scale, Aonidiella aurantii, resulted in the establishment on citrus of Aphytis chrysomphali. After further introductions in the 1940s and 1950s, this species was displaced by A. ling-nanensis, which in turn was displaced by A. melinus in the hot interior, but not the coastal, regions of southern California. The mechanism by which A. melinus out-competes A. lingnanensis has been extensively researched by R. Luck and colleagues.
In many other systems, however, different insect species coexist, even though they appear to use the same resource in the same way. For example, in 1981 J. H. Lawton and D. R. Strong examined the various coexisting herbivores of bracken fern and found no evidence for competition. A famous experiment in the rocky intertidal habitat reported by R. T. Paine in 1974 suggested a general explanation. The intertidal community consists of various species of filter feeders (e.g., barnacles) and other invertebrates that coexisted, even though they competed intensely for space on the rock surfaces. Paine removed starfish, the top predator in this system, and as a result, one species (a mussel) outcompeted and excluded all the other invertebrates and took over the site. Paine termed the starfish a keystone predator, meaning that it had dominant effect on the number of species present in the entire community. The implication was that such predators in many communities prevent competitive exclusion among their prey by maintaining densities below the level at which competition would cause one species to predominate.
Population and community ecologists frequently portray the interaction of organisms in a community in terms of trophic levels or food webs. At the bottom trophic level are the primary producers, the green plants that use photosynthesis to sequester energy from the sun. The next trophic level is occupied by herbivores that feed on the plants. Carnivores that feed on the herbivores or on other carnivores occupy higher trophic levels. A typical food web involving insects on collard plants is illustrated in Fig. 7 .
An influential paper by N. G. Hairston and colleagues in 1960 proclaimed that the importance of competition for resources, as opposed to regulation by natural enemies, varies with trophic level. These authors proposed that densities of primary producers are typically governed by competition for light, nutrients, or water. Herbivores, on the other hand, are typically regulated by their natural enemies at densities well below carrying capacity, so that competition for resources is unimportant. In contrast, carnivores typically limit the densities of their prey and thus are regulated by competition for resources. Regulation of population density by natural enemies has been termed “top-down” control. Regulation by way of competition for resources or by other interactions between an animal and its food supply has been termed “bottom-up” control.
The generalizations of Hairston and colleagues were widely criticized and many obvious exceptions exist, but variations on this idea have persisted. More recent versions have included effects of several levels of carnivores and other factors such as community productivity or environmental stress. Experimental manipulations, particularly in aquatic systems, have provided support for the general idea in the form of trophic cascades. For example, in 1990 M. E. Power reported the experimental exclusion of top carnivores (large fish) from a food web in a California river. The results were a 10-fold increase in smaller fish and predatory insects that in turn caused an 80% decrease in herbivores (larval chironomid midges) and a 3- to 120-fold increase in the primary producers (algae). These results were the opposite of those predicted by Hairston and coworkers because there were four trophic levels, instead of three. Omnivores that feed simultaneously on several trophic levels complicate our understanding of most natural food webs. Research in several agricultural crops shows that intraguild predation can cause counterintuitive effects of predators on herbivorous insects. For example, in 2001 W. E. Snyder and A. R. Ives showed that carabid predators in alfalfa feed on pea aphids. Since, however, they feed even more heavily on the aphid “mummies” that contain parasitoids of pea aphids, their net impact is to increase aphid densities.
The relative importance of top-down vs. bottom-up regulation of herbivores has been debated for several decades. A review of population studies by D. R. Strong and colleagues in 1984 concurred with Hairston and colleagues that competition among most insect herbivores was rare, because herbivore densities were typically kept far below carrying capacity by natural enemies. More recent reviews (e.g., by Denno et al., 1995) have challenged this view. One issue is that many plants have sophisticated chemical defenses and many plant parts, such as foliage, are nutrient poor. Many herbivores consume specialized plant parts that are either nutrient rich (e.g., seeds) or are poorly defended (e.g., new leaves). Competition for these resources may be intense. Furthermore, plants influence both the survival and fecundity of herbivores in many subtle ways. For example, all herbivores disperse and must locate suitable host plants; failure to find host plants may be a dominant source of mortality and may vary from one habitat to another. Spring-feeding foliage feeders must synchronize their emergence with that of host foliage; failure to synchronize may cause mortality or may reduce fecundity because of consumption of inadequate or poor-quality foliage. Such factors are rarely documented in life-table studies. For most insect herbivores, a mixture of top-down and bottom-up forces determines density.
TEMPORAL PATTERNS OF FLUCTUATION
Density fluctuations, whether they are large or small, may occur at erratic or at regular intervals. Simple population models of predators and prey or laboratory studies, as already discussed, often exhibit regular oscillations. Evidence, however, for regular oscillations in nature is rare. The density of most species fluctuates erratically (Fig. 8). This is not surprising because the density of most species is influenced by weather conditions in a multitude of ways. Except for obvious regularity of seasonal variation, weather conditions vary from week to week and year to year in ways that are mostly erratic.
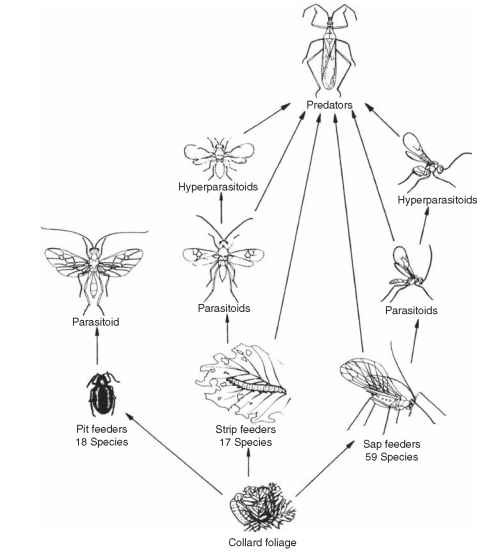
FIGURE 7 Schematic of arthropod food web in collards.
Furthermore, most species are influenced by a large suite of natural enemies. Predator-prey oscillations, such as those that occur in simple theoretical models or simple laboratory systems, become erratic and irregular when many natural enemies are involved.
Although the density fluctuations of most species are erratic, there are a few that exhibit regular cycles of abundance, similar to what is observed in laboratory populations or in theoretical models. For many others it is not obvious whether the fluctuations are or are not regular. For example, which of the insects in Fig. 8 have a regular component in their fluctuations, and what is the cycle period? Time-series analysis provides the statistical tool to answer these questions. Perhaps the most famous example among insects of regular cycles is that of the larch budmoth, Zeiraphera diniana, an insect that periodically defoliates larch forests in the European Alps (Fig. 9). The defoliator reaches peak density at 8- to 9-year intervals and seems to increase or decrease exponentially in the intervals between (linear on a log scale, as in Fig. 1B). The changes in budmoth density were associated with increases in both parasitism and mortality from a virus disease in what looked like a classic case of delayed density dependence. In 1981
R. M. Anderson and R. M. May proposed a host-pathogen model for this system that has served as a template for similar models of other insect host-pathogen systems. Anderson and May believed that the pathogen alone could account for the regular cycles. Other data suggested that effects of defoliation on host-plant quality, as well as genetic variation in the budmoth itself, may also account for the density oscillations. This famous example illustrates the difficulty in distinguishing cause from effect in the confluence of bottom-up and top-down forces that account for cyclic behavior in some population systems.
Prior to the 1970s, ecologists assumed that erratic fluctuation evident in most populations was caused by erratic weather conditions or other sources of randomness. They assumed that the density fluctuations embodied in mathematical models or in simple laboratory populations would have simple dynamics. Densities of such systems would either remain at equilibrium or exhibit regular oscillations about the equilibrium value, as in all the examples given earlier ( Figs. 5 and 6). The pioneering work on deterministic chaos by R. M. May in 1974 taught us otherwise. May studied the behavior of versions of the logistic equation appropriate for organisms with discrete

FIGURE 8 Sixty years of density fluctuations (plotted on a log scale) of four forest Lepidoptera in Europe.
FIGURE 9 Regular cycles of larch budmoth density in the European Alps.
or nonoverlapping generations (Fig. 10). There is a family of such models, of which the simplest is
![]()
where a is reproductive rate analogous to r of the continuous logistic, and Xt is density in generation t as a proportion of the carrying capacity K (i.e., Xt = Nt/K). When the reproductive rate was low (Fig. 10A) , the population remains at equilibrium. At higher values of a, the system alternates between high and low values, a
pattern known as a 2-point cycle (Fig. 10B). As a increases further, the system shifts to 4-point (Fig. 10C ) , and then 8-point, 2^ cycles. Above a = 3.57 however, an entirely new behavior, the chaotic regime, prevails, and densities fluctuate erratically without ever repeating themselves (Fig. 10D). These results had profound implications. They suggested that the erratic behavior characteristic of most natural populations (e.g., Fig. 8) might be due to the inherent mathematical properties of the interaction with natural enemies and other density-dependent effects, instead of resulting from random forces such as weather.
There ensued an effort to determine whether natural populations were indeed chaotic. Early studies concluded that most populations were not chaotic. These were based on attempts to fit natural populations to simple models and then to see whether the values of model parameters representing, for example, density dependence, time delays, or reproductive rate would elicit the expectation of chaotic behavior. The problem was that the conclusion depended on the particular model used, which was always a simplistic abstraction of the inevitably complicated dynamics of real populations. Subsequent investigators offered techniques that were more general and free of assuming particular population models. Applications of these techniques have indicated that some population systems are chaotic, but most are not.
SPATIAL PROCESSES
Species that are introduced into new habitats will spread from the point of introduction to surrounding areas in a pattern that frequently resembles concentric rings (Fig. 11 ). Theoretical population biologists, beginning with J. G. Skellam in 1951, have developed models of population spread that couple processes representing population growth with that of dispersal. Dispersal is typically modeled as a random movement process that is analogous to molecular diffusion.
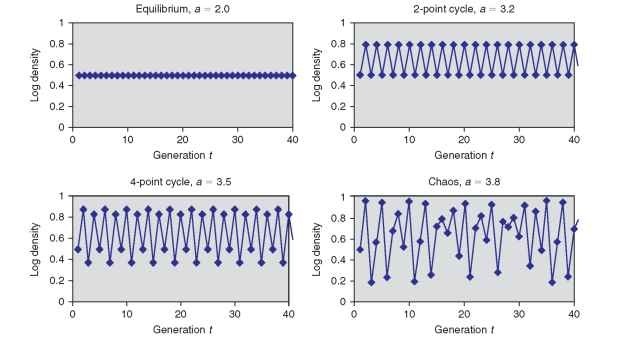
FIGURE 10 Density of a hypothetical population plotted vs. time for a version of the logistic equation appropriate for insects with discrete generations under different values of the reproductive rate a illustrating (A) a steady state, (B) a 2-point cycle, (C) a 4-point cycle, and (D) chaos.

FIGURE 11 Spread of the cassava green mite from its point of introduction near Kampala in 1971.
These models typically predict that the leading edge of the infestation forms a traveling wave that moves across the landscape at a constant speed in any given direction. As illustrated in Fig. 11, speed of movement will in fact vary markedly in different directions with differences in prevailing winds or with the presence of barriers such as the Sahara Desert.
Density fluctuations of different populations of the same species frequently exhibit spatial synchrony, meaning that densities go up and down together over a large region, as illustrated by gypsy moth Lymantria dispar, in the northeastern United States (Fig. 12). Since there are several possible causes of spatial synchrony, including dispersal of animals between populations, increases in density in one population will produce emigrants that trigger increases in surrounding populations. By far the most common cause of spatial synchrony, however, is the Moran effect, named after the individual who studied the synchrony of lynxes and hares in boreal Canada. In 1953 P. A. P. Moran showed mathematically that the density fluctuations of two or more populations will synchronize, provided they are governed by the same factors, such as the same natural enemies and are also influenced by some common factor such as the weather, which varies from year to year in the same way on a regional spatial scale. The important point is that although variations in weather may cause spatial synchrony, we should not infer that weather is also responsible for fluctuations in density, which might typically be caused by interactions with predators, pathogens, and parasitoids.
CONCLUSION
Population ecology forms the theoretical foundations upon which management of insects is based. Much has been learned from the development of mathematical models of population systems, studies
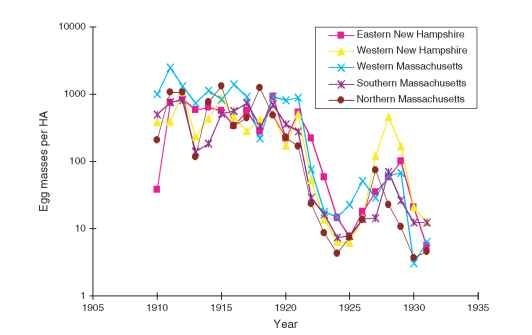
FIGURE 12 Spatial synchrony of gypsy moth populations in the northeastern United States. [Adapted from Campbell, R. W. (1981). In “The Gypsy Moth: Research Toward Integrated Pest Management” (Doane, C. C., and McManus, M. L., eds.), USDA For. Serv. Tech. Bull. 1584, pp. 65-86.
of laboratory populations, analyses of data from natural populations, and experimental manipulation of populations in the field. Despite decades of research, we are still far from understanding the population dynamics of most insects, even those such as gypsy moth or spruce budworm, which have been studied by several generations of researchers. Although various individuals have proposed theories to account for the dynamics of these species and have collected supporting data, rigorous demonstrations that these theories are correct elude us. For most insect species we have neither theories nor data to account for their population dynamics. The reason for this state of affairs is that it is extremely difficult to accurately measure the density of natural populations, especially when densities are low, and even more difficult to measure the impact of various factors causing mortality or variation in fecundity. Each insect and its natural enemies are embedded in a web of interactions whose intricacies must be disentangled. To understand how these intricacies vary over time, such information must be gathered for decades and coupled with experimental manipulations, that are often prohibitively expensive to conduct. The financial and human resources necessary to conduct such research are rarely assembled.
