Insect eyes are of two basic types: compound (or multifaceted) and simple (or single chambered). In adults, the principal organs of sight are nearly always compound eyes, although simple eyes—often quite good ones—are frequently present in imma-tures. Despite the major differences in their form and construction, compound and simple eyes perform essentially the same job of splitting up the incoming light according to its direction of origin (Fig. 1). Compound eyes are of two distinct and optically different kinds: apposition eyes, in which each receptor cluster has its own lens, and superposition eyes, in which the image at any point on the retina is the product of many lenses.
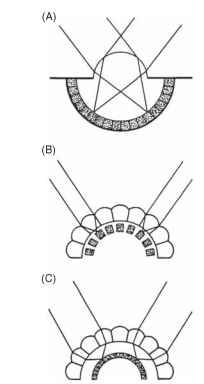
FIGURE 1 The three types of eye found in insects. (A) Simple, or single-chambered, (B) apposition compound, (C) superposition compound. The receptors are shown stippled.
APPOSITION EYES
History of Insect Optics
The facets of compound eyes of insects are too small to be resolved with the naked eye, and it required the invention of the microscope in the 17th century before they could be properly depicted. The process of working out how compound eyes functioned took more than two centuries from Robert Hooke’s first drawing of “The Grey Drone Fly” (probably a male horse fly) in his Micrographia of 1665 to the essentially modern account by Sigmund
Exner in 1891. The first person to look through the optical array of an insect eye was Antoni van Leeuwenhoek, and his observations caused a controversy that was not fully resolved until the 1960s. The following quotation comes from a letter from Leeuwenhoek to the Royal Society of London, which was published in 1695.
Last summer I looked at an insect’s cornea through my microscope. The cornea was mounted at some larger distance from the objective as it was usually done when observing small objects. Then I moved the burning flame of a candle up and down at such a distance from the cornea that the candle shed its light through it. What I observed by looking into the microscope were the inverted images of the burning flame: not one image, but some hundred images. As small as they were, I could see them all moving.
Evidently, each facet of the eye (at least in apposition eyes) does produce an inverted image, even though the geometry of the eye as a whole dictates that the overall image is erect (Fig. 1). What, then, does the insect see? Do the receptors (typically eight) beneath each lens resolve the inverted images, or do they just indicate the average intensity across the field of view of the ommatidium? (An ommatid-ium is the “unit” of a compound eye, consisting of the lens, receptors, and associated structures. See Fig. 2A.)
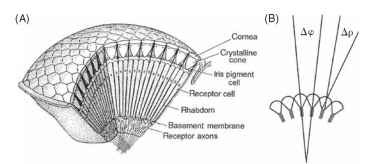
FIGURE 2 (A) Basic structure of an apposition eye, showing its construction from ommatidial elements. (B) Definitions of the interommatidial angle, Ay3, and rhabdom acceptance angle, Ap.
Remarkably, the answer depends on the animal. By the 1870s histological studies had shown that in most apposition eyes the eight receptor cells in each ommatidium contribute to a single radial structure, known as a rhabdom (Greek for rod; Figs. 2 and 3). Much later, in the 1950s, this material was found to be made up of photore-ceptive membrane covering large numbers of long narrow micro-villi, but even by the time that Exner wrote his monograph in 1891 it was clear that the rhabdom was the structure sensitive to light. Optically, each ommatidium works as follows. The inverted image that Leeuwenhoek saw is focused onto the distal tip of the rhabdom. Having a slightly higher refractive index than its surroundings, the rhabdom behaves as a light guide, so that the light that enters its distal tip travels down the structure, trapped by total internal reflection. Any spatial information in the image that enters the rhabdom tip is lost, scrambled by the multiple reflections within the light guide, so that the rhabdom itself acts as a photocell that averages all the light that enters it. Its field of view is defined, in geometric terms, by the angle that the tip subtends at the nodal point of the corneal lens (Ap; Fig. 2B), and in a typical apposition eye this acceptance angle is approximately the same as the angle between the ommatidial axes
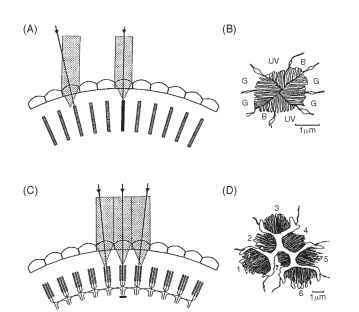
FIGURE 3 Optical comparison of an apposition eye (A, B) and a neural superposition eye (C, D). In an apposition eye each rhabdom (hatched) views light from a slightly different direction (arrows), and the rhabdoms (B), although made up from eight receptors, have a fused structure that acts as a single light guide. UV, B, and G indicate the receptor elements that respond to ultraviolet, blue, and green in an ommatidium from the eye of a worker bee. In neural superposition eyes, light from a single direction is imaged onto different rhab-domeres in adjacent ommatidia (C). The axons from all receptors imaging the same point collect together in the first synaptic layer (the lamina, Fig. 5) so that here the image has the same structure as in an ordinary apposition eye. The section (D) shows the arrangement of the separated rhabdomeres in an ommatidium from a fly. The six outer rhabdomeres (1-6) all send axons to different adjacent laminar “cartridges” (as in C). The central pair (7 overlying 8) bypass the lamina and go straight to the next ganglion, the medulla.
(the interommatidial angle, Aip Fig. 2B). Thus the field of view of one rhabdom abuts (or “apposes,” hence the name) the field of its neighbor, producing an overall erect image made up of a mosaic of adjacent fields of view.
Although the eight receptors that contribute to the rhabdom share the same visual field, it does not mean that they supply the same information. The labels UV, B, and G on the cross section of a bee rhabdom in Fig. 3B indicate the regions of the spectrum that the cells respond to best. Most insects have trichromatic color vision, just as humans do, although their visible spectrum is shifted toward shorter wavelengths compared with ours (Fig. 4). Some butterflies and dragonflies have four-color vision.
The second feature of the bee rhabdom (Fig. 3B) is that the microvilli making up the structure are arranged in orthogonal sets. It has been known since the work of Karl von Frisch in the 1940s that bees can navigate using the pattern of polarized light in the sky. This capacity arises from the way the photoreceptor molecules are arranged on the microvilli. A geometric consequence of the cylindrical shape of the microvilli is that there will be twice as many light-sensitive chromophore groups of the rhodopsin molecules aligned parallel to the long axis of each microvillus than at right angles to it. This, in turn, means that the receptors respond best to light polarized
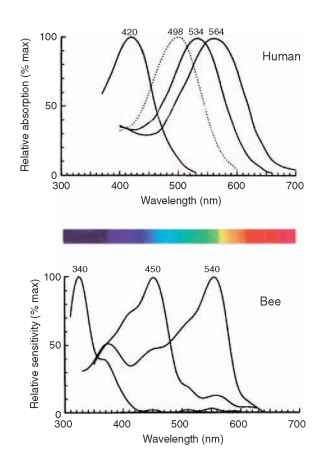
FIGURE 4 The spectral sensitivity curves for the three human cone mechanisms (and rods, dotted) and the corresponding three curves for a bee. The spectrum shows the colors as they appear to human eyes.
parallel to this axis. In fact bees use a special dorsal region of the eye (the POL area) to analyze sky polarization; in the rest of the eye the receptors are twisted to abolish polarization sensitivity, so that it does not interfere with color vision. Polarization vision is also used by some insects, such as the water bug Notonecta, to detect water surfaces, which polarize light strongly.
The description of apposition optics given above holds for most diurnal insects (e.g., bees, grasshoppers, and dragonflies), but it does not apply to the true (two-winged) flies, the Diptera. Since 1879, when Grenacher observed that the receptors in fly ommatidia have separate photoreceptive structures (rhabdomeres) that do not contribute to a common rhabdom, there had been suspicions that flies might actually be resolving the Leeuwenhoek images. In the focal plane of the lens of a fly ommatidium, the distal tips of the rhab-domeres are separated from each other and form a characteristic pattern (Fig. 3D) that resolves the image into seven parts (there are eight receptors, but the central pair lie one above the other). This raises the obvious question: how are these seven-pixel inverted images welded together to form the overall erect image, if indeed that is what occurs? Kuno Kirschfeld finally solved this conundrum in 1967. It turns out that the angle between the fields of view of adjacent rhabdomeres within an ommatidium (about 1.5° in a blow fly) is identical to the angle between neighboring ommatidial axes. Furthermore, the fields of each of the six peripheral rhabdomeres in one fly ommatidium are aligned, in the space around the fly, with the field of the central rhabdomere of one of the neighboring ommatidia (Fig. 3C). Thus, each point in space is viewed by seven rhabdomeres in seven adjacent ommatidia. What does this complicated and seemingly redundant arrangement achieve? To answer this it is necessary to know what happens to the signals from the seven receptors that view the same point, and that turns out to be the most astonishing part of the story. Beneath each ommatidium, the emerging receptor axon bundle undergoes a 180° twist before the individual neurons disperse to nearby regions of the first optic ganglion (the lamina) that correspond to the adjacent ommatidia. The net result of this impressive feat of neural knitting (Fig. 5) is that all the axons that “look at” the same point in space finish up making connections with the same cells in the lamina. Thus, as far as the lamina is concerned, the image is exactly the same as it would be in a conventional apposition eye, except that the signal, in terms of photon captures, is seven times stronger. One advantage of the extra signal is that it provides flies with a short period at dawn and dusk when they can see well, but when the eyesight of their predators and competitors is less sensitive and so less effective at detecting small objects.
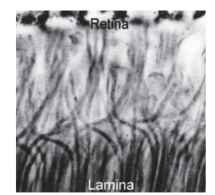
FIGURE 5 The interchange of axons that occurs between retina and lamina of a blow fly (Calliphora), which makes possible the neural superposition mechanism of Fig. 3C.
Kirschfeld called this arrangement ” neural superposition, ” because, as in optical superposition (see later), the contributions of a number of ommatidia are superimposed in the final image. One might ask: could the signal not have been made stronger simply by increasing the diameter of the rhabdom in a conventional apposition eye? Indeed it could, but that would mean increasing the rhab-dom acceptance angle (A/9; Fig. 2B) at the same time, which in turn would mean a loss of resolution for the eye as a whole. The beauty of the fly solution, and undoubtedly the reason why it evolved, is that it involves no increase in acceptance angle, provided the rhabdomeres are properly aligned. There are strong hints that something like neural superposition occurs in other insect groups (some beetles, earwigs, water bugs, and crane flies) but it is only in the advanced flies that the perfect nearest-neighbors arrangement is known to be achieved.
Imaging Mechanisms
The structures that form the images in the ommatidia of apposition eyes are quite varied (Fig. 6). In terrestrial insects, as in terrestrial vertebrates, the simplest way to produce an image is to make the cornea curved (Fig. 6A). Ordinary spherical-surface optics then
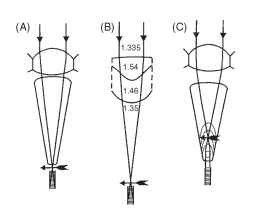
FIGURE 6 Four mechanisms of image formation in apposition eyes. (A) Corneal lens (bee, fly). (B) Multisurface lens (water bugs). (C) Lens/lens-cylinder afocal combination (butterflies). Details in text.
apply, and an image is formed about four radii of curvature behind the front face. In aquatic insects such as the water bug Notonecta, the external surface of the cornea has little power because of the reduction in refractive index difference (Fig. 6B). It is augmented by two other surfaces, the rear of the lens and an unusually curved interface in the center of the lens whose function may be to correct one of the defects of spherical surfaces— spherical aberration.
The eyes of butterflies, which resemble ordinary apposition eyes in nearly all respects, have an optical system that is subtly different from the arrangement in Fig. 6A. Instead of forming an image at the rhabdom tip, as in the eye of a bee or locust, the image lies within the crystalline cone. The proximal part of the cone contains a very powerful lens cylinder that makes the focused light parallel again, so that it reaches the rhabdom as a beam that just fits the rhab-dom (Figs. 6C and 17). This arrangement, known as afocal apposition because there is no external focus, has much in common with the superposition optical system of moths, to which butterflies are closely related, and will be considered later.
Resolution
For any eye, the resolution of the image seen by the brain is determined by the fineness with which the ommatidial mosaic samples the environment, represented by the interommatidial angle, Ace (Fig. 2B), and by the quality of the image received by each rhab-dom, represented by the rhabdom acceptance angle A/ ( Fig. 2B ). (Although the eight receptors that contribute to each rhabdom usually have different spectral and polarization responses, they all share a common field of view.) In asymmetric eyes (which most are) At£ may be different along different axes of the facet array, but for present purposes At£ is taken to be the average of the angle measured along each of the three axes of the array. In the central region of a bee eye, At£ is about 1.7° . An extensive table of values can be found in a recent review by Land in 1997.
One would expect that apposition eyes would show a rough match between the interommatidial angle and the acceptance angle (A/ ) of a single rhabdom, the argument being that no individual rhabdom can resolve detail finer than Ap, so there is no point spacing the directions of view of ommatidia closer than this angle. The acceptance angle Ap is actually a combination of the contributions of ray and wave optics (Fig. 7A). Geometrically, Apray is the angle subtended by the rhabdom tip at the nodal point of the facet lens,
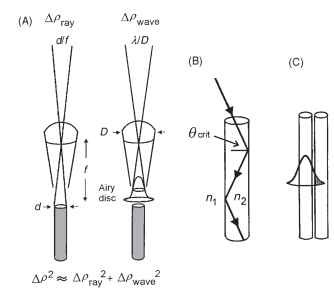
FIGURE 7 (A) The acceptance angle (Ap) of an ommatidium results from a combination of the Airy diffraction pattern (point-spread function), given by A/D (right), and the geometrical angular width of the rhabdom (d/f) at the nodal point of the lens (left). (B) Light is trapped in a rhabdom by total internal reflection, which occurs when the angle the light makes with a normal to the wall is greater than the critical angle, given by sin #crit = n1/n2, the ratio of the refractive indices outside and inside the rhabdom. A typical rhabdom can trap a cone of light about 22° wide. (C) In narrow light-guiding structures some of the light is actually outside the fiber, and can potentially be caught by adjacent fibers and so spoil resolution.
i.e., the rhabdom diameter divided by the focal length (d/f radians). Typical values (for a bee) are 2 |im for d and 60 |im forf, which makes Apray 0.033 radians, or 1.9°. In wave optics, the limit to image quality is set by diffraction, specifically by the angle subtended by the Airy disk (the diffraction image of a point source), and this is given by A/D radians. If the wavelength (A) is 0.5|im and the facet diameter (D) is 25|im, then Apwave is 0.02 radians, or 1.1°. To obtain the final value for Ap, Apray and Apwave have to be combined, and unfortunately the proper way of doing this (convolution, taking the wave-guide properties of the rhabdom into account) is very complicated. A simple approximation is given by Ap2 = Ap2ay + Apwave. This is adequate for most purposes but tends to overestimate Ap slightly. Using this approximation, Ap for the bee data is 2.2°, somewhat larger than Ap. Typically in light-adapted diurnal insects the ratio of Ap to Ap is about 1:1.
The neural superposition eyes of dipterans have an additional constraint, namely that the separation of the tips of the rhabdomeres must match the interommatidial angle. In a house fly, Ap is about 2°, and with an ommatidial focal length of 70 |im, this means that the tip separation must be 2.4 |im, which does not leave a great deal of room (Fig. 3D). Because narrow light guides, such as rhabdomeres, tend to be “leaky,” with a substantial fraction of the light energy outside the guide itself (Fig. 7C), there needs to be an adequate gap between one rhabdomere and the next to prevent cross talk. In flies there is a 1-|im gap between adjacent rhabdomeres (Fig. 3D), which means that the rhabdomeres themselves must be very narrow. They have a distal tip diameter that is also about 1 |im, making them among the narrowest photoreceptors in any animal. In most other respects, however, neural superposition eyes are optically similar to other apposition eyes.
Diffraction and Eye Size
In a short and remarkable article titled “Insect sight and the defining power of compound eyes,” published in 1894, Henry Mallock, an optical instrument maker, described insect vision in these terms: “The best of the eyes… would give a picture about as good as if executed in rather coarse wool-work and viewed at a distance of a foot.”
Why is insect vision so poor? The problem, as Mallock recognized for the first time, is diffraction. Compound eyes have very small lenses compared with the lenses of single-chambered eyes, and because the size of the diffraction blur circle (the Airy disk) is inversely proportional to aperture diameter, the blur circles are large and the resolution correspondingly poor (Fig. 7A). A 25-|im diameter facet of a bee produces an Airy disc that is just over 1° wide in angular terms. One degree is about the size of a thumbnail at arm’s length, so one can imagine a bee’s world made up of pixels of about that size. In terms of the acuity of our own eyes (Ap about 0.01°), this is not very good at all.
Mallock’s article goes on to discuss what a compound eye with human resolution would look like, and he came to the astonishing conclusion that it would need to be more than 20 m in diameter, or bigger than a house. The reason for this is clear: the human eye achieves high resolution by having a daylight pupil diameter of 2 mm, 80 times the diameter of a bee lens. For a bee to have the same resolution, diffraction requires that all its lenses would need to have this diameter, and to exploit all the detail in the scene they would need to be spaced at 0.5 arcmin angular intervals, the same as the receptors in our fovea. In a spherical eye, the interommatidial angle (Ap) is the angle subtended by one lens diameter at the center of the eye (D/r radians, where r is the eye radius), which gives r = D/Ap. With Ap = 0.5 arcmin of arc (0.000145 radians; 1 radian = 57.3° and 1° = 60 arcmin), and D = 2 mm, the radius of curvature will be 13.8 m and the diameter twice this. (Kirschfeld has pointed out that this calculation is a little unfair because resolution in the human eye falls off dramatically away from the fovea, to a tenth of its maximum value at 20° from the fovea, and even less farther out. Taking this into account the “human” compound eye can be shrunk in size considerably, to an irreducible 1 m diameter, which still looks very clumsy). Dragonflies seem to approach the limit of what it is possible with an apposition eye. Their eyes are 8 mm or more in diameter, have up to 30,000 facets each, and resolve about 0.25° in their most acute region. This is still poor compared with what is achievable by any camera-type eye of the same diameter.
The outcome of this discussion is that it is very hard for an apposition eye to improve its resolution; it simply gets too big. Space is thus at a premium; a little extra resolution here must be bought by a bit less there, and for this reason the different visual priorities of arthropods with different lifestyles show up in the distribution of interommatidial angles, and often facet sizes, across the eye.
Sensitivity
The sensitivity of an eye is the ratio of the amount of light received by a single photoreceptor to the amount emitted by the surface that eye is imaging. It can be used to work out the numbers of photons that individual receptors receive, and this determines the way in which the eye will perform under dim light conditions. Sensitivity can be calculated from the formula S = 0.62 D2 Ap2, where D is the lens diameter and Ap the rhabdom acceptance angle ( Figs. 2B and 7A ) (we ignore the effect of receptor length here). Although D is roughly 100 times greater in a human eye than in a bee ommatidium, Ap is about 100 times smaller (approximately
0.015° compared with 1.5°), so that the value of S is very similar in the bee and the human. Thus, the range of illumination conditions over which an insect with an apposition eye can operate is similar to that of a mammal using its cone system. Mammals can also see at much lower intensities, by pooling the responses of rods over quite large retinal areas (effectively increasing Ap). It is unlikely that pooling occurs to any great extent in insect eyes.
When discussing sensitivity, ” adaptation ” can have two meanings. Different eyes may be adapted in the evolutionary sense to work permanently under conditions of high or low illumination, e.g., night or day, deep sea or surface. Alternatively, the same eye can be said to be light- or dark-adapted via reversible and temporary changes in its optical anatomy. In both cases, the above equation is the key to interpreting changes and differences.
Light and Dark Adaptation
Temporary light and dark adaptation mechanisms take a number of forms in apposition eyes. Some are illustrated in Fig. 8 and include the following: (A) an iris mechanism just above the distal tip
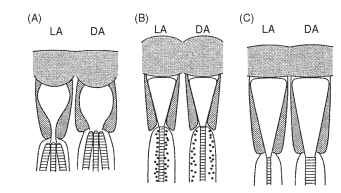
FIGURE 8 Three mechanisms of dark adaptation in apposition eyes of insects (see text).
of the rhabdom that restricts the effective value of Ap. In the case of crane flies (Tipulidae), which have an arrangement of six outer and two central rhabdomeres, the iris cuts off the outer six in the light, leaving only the central pair. (B) A “longitudinal pupil” consisting of large numbers of very small pigment granules that move into the region immediately around the rhabdom in the light and withdraw in the dark is a second form. The main effect of this is to absorb the wave-guided light that travels just outside the rhabdom. This is replaced with light within the rhabdom, and this is absorbed in turn, so that light is progressively “bled” out of the rhabdom. This mechanism is particularly important in higher Diptera (house flies, etc.) and in butterflies, and it can work in a matter of seconds. (C) The rhabdom dimensions may themselves change, usually over a period of hours. This mechanism may involve the resynthesis of photore-ceptive membrane in the dark and its sequestration in the light. In addition to these changes there are electrical and enzymatic changes in the receptors themselves that alter the gain of transduction and increase response time in the dark.
Ecological Variations in Apposition Design
As we have seen, the optical design of apposition eyes means that there is no spare room on the head surface, and what there is needs to be used as efficiently as possible. A survey of the apposition eyes of insects and crustaceans leads to the conclusion that there are three main patterns of acuity distribution that one can identify fairly easily. These are identified in Fig. 9, which illustrates the ecological reasons for these patterns (Fig. 9A-9C) and examples of the distributions themselves (Fig. 9D-9F). Figure 9D shows the pattern related to the motion across the eye encountered in forward locomotion, especially flight. Figure 9E has an “acute zone” associated with predation or sex, these zones sometimes developing into separate components of a double eye. In Fig. 9F the narrow horizontal strip of high resolution is associated with environments such as water surfaces and sand flats, where almost all important activity takes place around the horizon.

FIGURE 9 (A-C) Three situations that lead to asymmetries in the distribution of resolution in apposition compound eyes. (A) Flight through vegetation. (B) Chasing mates or prey. (C) Flight close to flat surfaces. (D-F) Plots of the density of ommatidial axes around the eyes of three insects, corresponding to the three situations in A-C. (D) Locust (forward flight pattern). (E) Drone bee (chasing females). (F) Water strider (hunting on water surface). Contours show the numbers of ommatidial axes per square degree of space around the animal.
THE FORWARD FLIGHT PATTERN
When an animal is moving through the world, the objects in the world appear to move backward across the eye. Objects to the sides move faster than those in front, and there is a point in the direction of the animal’s travel (the “focus of expansion”) where there is no image motion. Objects farther away move more slowly than near objects. Clearly, near objects to the side are likely to move so fast across the retina as to cause blurring, and if this is the case it would be economical to use fewer receptors there, as high resolution is not usable. For a bee or butterfly flying half a meter from foliage, the blur streak can be estimated to be about 2.3° long. It follows that there is little point in having lateral-pointing receptors closer together than 2 or 3°, however good the resolution at the front of the eye may be. This seems to be borne out in practice. In the butterfly Heteronympha merope, e.g., the horizontal interomma-tidial angle decreases from 1.4° in front to 2.6° at the side. Bees, butterflies, and acridid grasshoppers are flying insects, and their eyes all show decreasing horizontal interommatidial angles from front to rear, consistent with these ideas. Nonflying insects, e.g., many tettigonid grasshoppers, have more or less spherical eyes, without this gradient. In all the flying groups there is another, separate gradient of vertical interommatidial angles; they are smallest around the eye’s equator and increase toward both dorsal and ventral poles. This results in a band around the equator with enhanced vertical acuity. The most likely reason for this vertical gradient is that the region around the eye’s equator contains the highest density of information important to the animal, especially if it is an insect that feeds on flowers.
The combined effects of these two gradients on the overall density of ommatidial axes are shown for a locust in Fig. 9D, in which the contours represent the number of ommatidial axes per square degree on the sphere surrounding the animal. Worker bees and female blow flies (Calliphora) show a similar pattern, although in male flies and drone honey bees, this pattern is distorted to give a more pronounced acute zone concerned with mate capture (also Fig. 9E).
ACUTE ZONES CONCERNED WITH PREY CAPTURE
AND MATING Many insects have a forward- or upward-pointing region of high acuity, related either to the capture of other insect prey or to the pursuit in flight of females by males (Fig. 9E). When both sexes have the specialization (mantids, dragonflies, robber flies), predation is the reason, but more commonly it is only the male that has the acute zone (simuliid black flies, hover flies, mayflies, drone bees), indicating a role in sexual pursuit. The acute zones vary considerably. In male house flies and blow flies, they may involve little more than a local increase in the acuity of the “forward flight” acute zone common to both sexes (see earlier). However, in other insects the acute zone may be in a separate eye, as is the case with the dorsal eyes of male bibionid flies (Fig. 10B). In these more extreme double eyes, the upward-pointing part is often specialized for detecting other small animals against the sky.
Good examples of forward-directed acute zones are found in the praying mantids, predators in which both sexes ambush prey. The eyes have large, binocularly overlapping acute zones that are used to center potential prey before it is struck with the spiked forelegs. Mantids provide the only known example in insects in which prey distance is determined by binocular triangulation. The interommatid-ial angle (Ace) in Tenodera australasiae varies from 0.6° in the acute zone center to 2.5° laterally. Facet diameters decrease from 50 |im in the acute zone to 35 |im peripherally, but this is less of a decrease than would be expected from diffraction considerations alone.
In many male dipterans an acute zone associated with sexual pursuit is typically situated 20-30° above the flight direction. In Calliphora flies it is characterized by a low value for At£ of 1.07° compared with 1.28° in the female. In house flies and probably in other flies there are also anatomical differences at the receptor level that suggest that this region (it has been called the “love spot”) is specifically adapted for improved sensitivity. This is no doubt caused by the very fast response times required for high-speed chasing. Male flies also have a number of “male-specific” interneurons in the optic ganglia, which are undoubtedly involved in the organization of pursuit behavior.
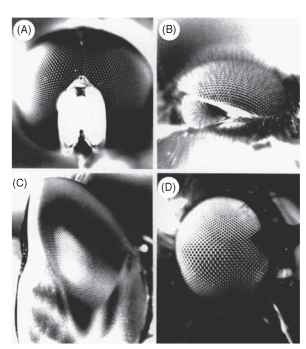
FIGURE 10 Eyes in which facet size reflects local resolution. Paradoxically, large facets produce high resolution. (A) Syritta (syr-phid male), (B) Dilophus (bibionid male), (C) Aeshna (dragonfly), (D) Hilara (empid fly). See text.
In the small hover fly Syritta pipiens the sex difference is particularly striking. In the male’s acute zone, Aip is about 0.6° . nearly three times smaller than elsewhere in the eye or anywhere in the female eye (Fig. 10A). Drone bees have a similar anterodorsal acute zone, where the density of ommatidial axes is three to four times greater than anywhere in the female eye (Fig. 9E) . They use this region when they chase the queen and can be induced to chase a dummy queen on a string subtending only 0.32°, much smaller than the ommatidial acceptance angle of 1.2°. This implies that the trigger for pursuit is a brief decrease of about 6% in the intensity received by single rhabdoms.
Most of the animals just discussed have to detect their prey or mates against a background of foliage, a far from easy task. However, many insects have simplified the problem by using the sky as a background, against which any nonluminous object becomes a dark spot. Thus, one finds not only upward-pointing acute zones but also double eyes with one component directed skyward (Fig. 10B and 10C). For example, dragonflies hunt other insects on the wing and have acute zones with a variety of configurations. Many in fact have two acute zones, one forward pointing, and presumably concerned with forward flight as discussed above, and another directed dorsally and used to detect prey. The migratory, fast-flying aeschnids have the largest eyes and most impressive acute zones. Exactly 28,672 ommatidia have been counted in one eye of Anax Junius, which has the smallest interommatidial angles of any insect (0.24° in the dorsal acute zone) and facets of corresponding size (62 |im). The dorsal acute zone takes the form of a narrow band of high resolution extending across the upper eye along a great circle, 50- 60 ° up from the forward direction. The axis density (five per square degree) is twice that in the forward acute zone and five times higher than in a male blow fly. The dorsal acute zone is easily visible as a wedge of enlarged facets (Fig. 10C). Presumably the great high-acuity stripe in Anax is used to trawl through the air, picking out insects against the sky much as the scan line on a radar set picks up aircraft.
Simuliid flies have divided eyes and use the upper part to detect potential mates against the sky. They can do this at a distance of 0.5 m, when a female subtends an angle of only 0.2° , As in drone bees, this is a small fraction of an acceptance angle. The eyes of male bibionid flies are similarly divided (Fig. 10B), with larger facets and smaller interommatidial angles in the dorsal eye (1.6° compared with 3.7°, in Bibio marci). The upper eyes are used exclusively for the detection of females; movement of stripes around the lower eye evokes a strong optomotor turning response (the almost universal visual behavior used by insects to prevent involuntary rotation) but the dorsal eye is quite unresponsive to this kind of stimulus.
HORIZONTAL ACUTE ZONES
As we have seen, many flying insects have a zone of increased vertical acuity around the horizon, no doubt reflecting the visual importance of this part of the surroundings. The visual field of the locust in Fig. 9A shows this clearly. There are environments where this region is even more important.
Insects that fly over water have a similarly narrow equatorial field of interest. Empid flies hunt close to the surfaces of ponds, again looking for stranded insects, and they have a horizontal acute zone that can be recognized by a linear region of enlarged facets around the eye (Fig. 10D). In Rhamphomyia tephraea, vertical interommatidial angles are only 0.5° in this 15°-high region, rising to 2° above and below it.
Water surfaces themselves provide a similarly constrained field of view, and water striders (Gerris) that hunt prey stranded in the surface film have a narrow acute band imaging this region, as shown in Fig. 9F. This has a height of only about 10°, centered on the horizon, and within this the vertical interommatidial angle in the frontal region is only 0.55°, which is close to the diffraction limit and impressive in an eye with only 920 ommatidia.
SUPERPOSITION EYES
The Nature of Superposition Imagery From the outside, apposition and superposition eyes are almost indistinguishable. Both are convex structures with facets of similar dimensions and are clearly variants of the same general design. But there the resemblance ends. Internally, there are several crucial anatomical differences: the retina is a single sheet, not broken up into discrete ommatidial units as in apposition eyes, and it lies deep in the eye, typically about halfway between the center of curvature and the cornea. Between the retina and the optical structures beneath the cornea there is a zone with very little in it, the clear zone, across which rays are focused—the equivalent of the vitreous space in a camera-type eye (Fig. 11). The optical devices themselves are complex—tn insects they are nearly always tiny refracting telescopes—although to a cursory examination most do not look very different from the lens structures of apposition eyes.
The real surprise is optical. All superposition eyes produce a single deep-lying erect image in the vicinity of the retina. This distinguishes them not only from apposition eyes, which have multiple inverted images, but also from camera-type eyes in which the image is inverted. Clearly, we are dealing here with something quite out of the ordinary. Around the turn of the 20th century there were a number of successful attempts to photograph these images. A recent attempt by the author to re-create this photographic feat, in a firefly eye, is shown in Fig. 12 (right), in which the single erect image should be contrasted with the multiple inverted images of an eye of the apposition type (Fig. 12, left). It turns out that it is important to
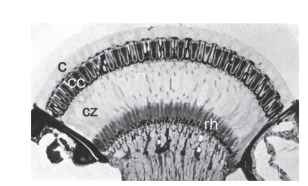
FIGURE 11 Section through the superposition eye of a dung beetle (Onitis westermanni). c, cornea; cc, crystalline cones; cz, clear zone; rh, rhabdoms.
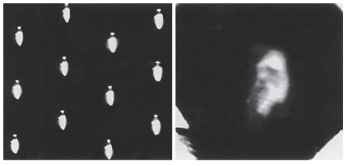
FIGURE 12 Left: Apposition-type inverted images photographed behind the cleaned cornea of a robber fly (Asilidae). Right: Photograph of an influential 19th century naturalist, taken through the superposition optics of the cleaned cornea of a firefly (Photuris sp.).
use a beetle (such as a firefly) for this. Other insects, in particular moths, have superposition eyes but there the optical structures that create the image are not joined to the cornea, and they are swept away when the eye is cleaned to make a lens for photography. In beetles, however, the optical elements are continuous with the cornea and so survive the removal of the eye’s internal structures.
The credit for the discovery and elucidation of this remarkable piece of optics is due to Sigmund Exner, who worked on the problem throughout the 1880s and published his complete findings in 1891. Exner showed that the only way an erect image could be formed was for the optical elements to behave in a rather strange way, as shown in Fig. 13A. Basically what each has to do is not form an image from a parallel beam as in a conventional lens, but redirect light back across the element’s axis, to form another parallel beam on the same side of the axis (Fig. 13B). Exner realized that although a single lens would not do the job, a two-lens telescope would, and he went on to demonstrate (as well as he could with the technology of the time) that such structures were indeed present in the superposition eyes of insects.
Telescopes and Lens Cylinders
In a lens-based superposition eye, the optical elements need to act as simple inverting telescopes that redirect the entering beam of light back across the axis, as shown in Fig. 13C , The most straightforward way to do this is to have two lenses separated by the sum of their individual focal lengths, with an image plane between them (Fig. 13C). Exner realized that, given plausible refractive indices and
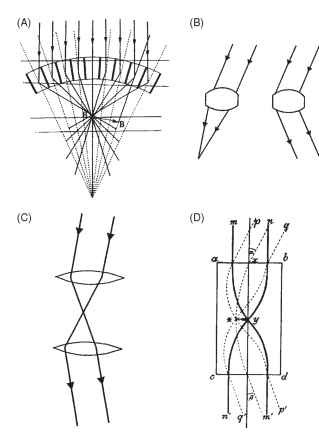
FIGURE 13 (A) Sigmund Exner’s diagram of ray paths in a superposition eye. Note that the rays are bent in a “dog-leg” path by the optical elements. (B) An ordinary lens (left) will not produce the ray bending at the right, as required in (A). (C) A two-lens telescope is needed to redirect a light beam back to the same side of the axis, as in (A). (D) Exner proposed a lens cylinder equivalent to the telescope, in which rays are bent within the structure by a parabolic gradient of refractive index, highest in the center.
the curvatures of the structures revealed by histology, there was not enough ray-bending power in each element of a beetle eye to make this possible. He came up with the idea that structures must have an internal refractive index gradient similar to that in the Limulus horseshoe crab eye. The result would be that most of the ray bending would occur within the tissue, rather than at its external surfaces. The pure form of this structure, a flat-ended cylinder with a radial parabolic refractive index gradient, Exner called a lens cylinder. He showed that, depending on its length, it could act as a single lens or as a pair of lenses making up an inverting telescope of the kind required for superposition optics (Fig. 13D ) . Although Exner did not have the means in his time of establishing whether beetles and moths had optical elements with the required refractive index gradient, numerous studies since the advent of interference microscopy have shown that his brilliant conjecture was correct.
Resolution and Sensitivity
The geometry of a superposition eye is shown in Fig. 14. The peculiarities of this type of image formation mean that the nodal point of the eye (the point through which rays pass undeviated) is at the center of curvature, and the focal length is the distance out from
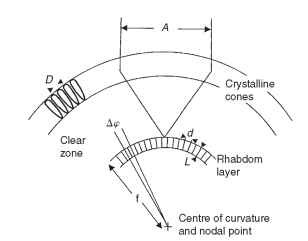
FIGURE 14 Optical definitions that apply to superposition eyes. D, facet diameter; A, superposition aperture; Ap, interreceptor angle (compare Fig. 2B); d, rhabdom diameter; L, rhabdom length; f, focal length.
the center to the image. The interrhabdom angle (Ap) is s/f, where s is the rhabdom separation, just as in a camera-type eye. As in apposition eyes, the rhabdom acceptance angle is a combination of the geometrical subtense of a rhabdom (d/f) and the width of the blur circle provided by the optics (Fig. 7A).
In the past, there has been a belief that superposition eyes suffer from poor resolution, mainly because of the difficulty of conceiving how the large numbers of ray bundles contributing to a single point on the image could be directed there with sufficient accuracy. However, this reputation seems not to be justified, except perhaps in extreme cases. A careful study by Peter McIntyre and Stan Caveney on the eyes of dung beetles that fly at different times of the day and night found that in the day-flying Onitis belial about 50 optical elements (the effective superposition aperture) contributed to the image at any one point, and in the nocturnal O. aygulus the number was close to 300. O. belial had a calculated rhabdom acceptance angle (Ap) of 2.2°, which is comparable with values from many apposition eyes, and in O. aygulus Ap was somewhat larger, 3.0°, which is still quite impressive for an eye with such a huge aperture. These modeling studies have since been confirmed by electrophysiological recordings from single receptors. In the Australian day-flying moth Phalanoides tristifica, the image quality has been measured directly with an ophthalmoscopic method that uses the eye’s own optics to view the retina and images on it. The result was that Ap, the acceptance angle of a rhabdom when viewing a point in space, was 1.58° , of which optical blur contributed only 1.28°.This is itself only slightly larger than the half-width of the Airy diffraction image from a single facet. Thus, a superposition eye in which 140 elements contribute to a point image has optics that are almost as good as is physically possible. (Although the superposition pupil is many times wider than an individual facet, it does not behave for diffraction purposes as a single large lens, and the Airy disk diameter depends on the diameter of single facets, just as in apposition eyes.)
Size for size, superposition eyes are more sensitive than apposition eyes, which is why they are most commonly encountered in animals such as moths and fireflies that are active at night. For an apposition eye and a superposition eye of the same size and the same resolution, the sensitivity of the superposition eye (with an aperture 10 facets wide) is 100 times that of the apposition eye, meaning that it will work just as well at light levels 100 times lower.
Eye Glow and the Superposition Pupil
Most moths have a reflecting layer (tapetum) behind the rhab-doms. Its function is the same as the tapetum in the eye of a cat: to double the light path through the photoreceptors and so to improve their photon catch. In some diurnal moths, a reflector also surrounds each rhabdom, optically isolating it from its neighbors. In dark-adapted eyes, the tapetum causes the eye to glow when viewed from the same direction as the illuminating beam (Fig. 15). In some diurnal moths, such as the sphingid Macroglossum. the glow is always visible. The mechanism is similar to that in a cat’s eye. The optical system forms a point image of the light source on the tapetum, or close to it, and this point acts as an emitter of light which, on passing through the optics again, emerges as a roughly parallel beam.
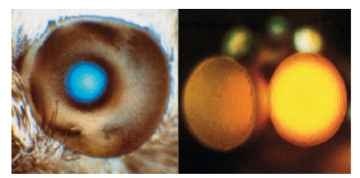
FIGURE 15 Left: Blue light reflected from the tapertum of the day-flying hummingbird hawk moth (Macroglossum). The bright area corresponds to the superposition pupil. Right: Superposition dorsal eyes of a male mayfly (Centroptilum). The yellow color is not from a tapetum, but results from the scattering of long wavelengths by screening pigment.
If the optics are good, that is to say they really do bring a parallel beam to a point in the image, then the patch of glow seen at the surface of the eye will have the same diameter as the beam that entered the eye. This is the superposition pupil (i.e., the amount of eye surface from which rays contribute to each point on the image; Fig. 15). Eye glow can also provide a useful test of image quality. If the glow can be seen only over a narrow angle (a few degrees) from the direction of the illuminating beam, then the retinal image must itself be very small. On the other hand, if the glow can be seen over a wide angle, this indicates either that there is a large blur circle on the retina or that the tapetum is situated a long way from the focus.
Light and Dark Adaptation
The high sensitivity of most superposition eyes means that they must protect their visual pigment in daylight and so need adaptation mechanisms that can reduce image brightness by several orders of magnitude. The main mechanism of light adaptation in superposition eyes consists of pigment movements that result in the progressive interception of rays from the outer zones of the superposition pupil (Fig. 16 ). This reduction may ultimately result in light from only a single facet reaching a single point in the image, which is essentially the apposition condition.
The eye glow (Fig. 15) provides a means of monitoring the process of light and dark adaptation. As oblique rays across the clear zone are cut off during light adaptation (Fig. 16) , the brilliance of the glow and the size of the patch are reduced, often disappearing completely. In the dark, these slowly return. In insects with refracting
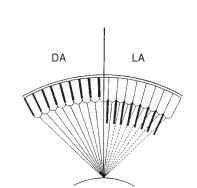
FIGURE 16 Mechanism of dark and light adaptation (DA, LA) in superposition eyes. Screening pigment migrates inward, cutting off the outer rays in the image-forming bundle.
superposition eyes, the main pigment movement is a longitudinal inward migration of granules in both the primary and the secondary pigment cells. In the dark, the granules are bunched up between the crystalline cones, and with the onset of light they extend inward, over a matter of minutes, to occupy much of the clear zone.
Interestingly, the trigger for pigment migration in some moths is not provided by photoreception in the rhabdoms themselves. In the crepuscular sphingid moth Deilephila, a region immediately beneath each crystalline cone initiates pigment migration, when illuminated with ultraviolet light, and the much deeper lying rhabdoms are not involved. However, in the owl fly Ascalaphus, a day-flying neuropteran with double superposition eyes, the pigment movements can be triggered from both the region below the cones and the rhabdoms themselves.
Single and Double Eyes
In superposition eyes, major departures from spherical symmetry are rare because the geometry of the eye is constrained by the shared optics (the hummingbird hawk moth Macroglossum is an exception in this respect, with a visibly asymmetric eye, but excellent resolution everywhere). One way around this problem is the use of double eyes, in which each part is essentially separate from the other and has its own radius of curvature. Although common among crustacean groups such as mysids and euphausiids, double superposition eyes are uncommon among insects. As mentioned earlier, owl flies (Ascalaphus) have double superposition eyes. Male mayflies have a pair of dorsal superposition eyes, which they use for sighting females against the sky, in a way similar to that of bibionid flies (Fig. 10B). However, the lower eyes, present in both sexes and responsible for other visual activities, are of the apposition type. The field of view of the dorsal eye is small, and it is adjusted to the environmental circumstances of the species; those species swarming in woods with small gaps in the canopy have the narrowest fields.
Afocal Apposition: The Eyes of Butterflies
Butterflies and moths are classified together in the Lepidoptera and are undoubtedly very closely related. Most butterflies [skippers (Hesperidae) are the exception] have eyes that behave in most respects as apposition eyes. They have long narrow rhabdoms abutting the bases of the crystalline cones, no clear zone, and complex pseudopupils. Many moths, on the other hand, have refracting superposition eyes with wide, deep-lying rhabdoms, clear zones, and eye glow. Transitions between the eye types must have occurred a number of times within the moths, as well as between moths and butterflies. A very similar picture emerges in the beetles, most of which have apposition eyes, but a substantial number of nocturnal and crepuscular groups, including the dung beetles and the fireflies, have superposition optics.
It is not very easy to see how it is possible to get from one type of eye to the other, without going through an intermediate that does not work. Apposition eyes use simple lenses and superposition eyes two-lens telescopes (or the equivalent lens cylinder devices), and there does not seem to be much room for compromise. In the case of butterflies we do know the answer: in 1984 Dan-Eric Nilsson and his colleagues discovered that their apposition eyes actually have an extreme form of superposition optics in the ommatidia, in which the proximal lens in each telescopic pair has become not weaker, as one might have guessed, but extremely powerful (see Fig. 6C).
The way this works is shown in Fig. 17A. As in a normal superposition eye, a combination of the curved cornea and a weak lens cylinder in the distal region of each crystalline cone results in the formation of an image within the crystalline cone, about 10 |im in front of its proximal tip. This focused light then encounters a lens with an extraordinarily short focal length, about 5 |im. The discovery of this lens involved taking thin frozen sections from the tiny region at the base of the crystalline cone and examining their image-forming properties. The last 10 |im of the cone produced excellent images. The effect of this second lens is to bring the light focused by the first (distal) lens back into a parallel beam, just as in a superposition eye. The essential difference is that, whereas in a superposition eye the magnification of the telescopic pair of lenses rarely exceeds -2, here it is much greater. The large difference in the focal length of the distal and proximal lenses gives an overall magnification of -6.4 in the nymphalid butterfly Heteronympha merope.
This high magnification has two important consequences, illustrated in Fig. 17B , The first is that the beam that emerges from the proximal tip makes an angle with the axis that is 6.4 times greater than the beam that entered the facet from outside. A ray making an angle of 1° with the facet axis emerges at 6.4°, and similarly a beam 3° wide at the cornea emerges into the rhabdom as a 19.2°-wide beam. The significance of this is that a rhabdom with a refractive index of 1.36 will just contain (by total internal reflection; Fig. 7B) a beam 22° wide, which in turn means that the acceptance angle of the ommatidium will be limited to just over 3°: light making higher angles with the rhabdom wall will escape and be absorbed by the surrounding pigment. Thus, in this kind of eye, the ommatidial acceptance angle is limited principally by the refractive index of the rhabdom, not (as in a conventional apposition eye) by its diameter (Fig. 7A). The second effect of the magnification is to reduce the diameter of the beam leaving the base of the crystalline cone by a factor of about 9 (angular magnification X refractive index), compared with that entering the facet. The entering beam is limited by the facet diameter, typically about 20 |im. The beam leaving the crystalline cone and entering the rhabdom is squashed down to a diameter of 2.1 |im, which is indeed close to the diameter of a butterfly rhabdom. Thus rhabdom diameter and facet diameter are related and between them determine the effective aperture of the omma-tidium and hence its sensitivity. Bright-light butterflies tend to have smaller facets (20 |im) and narrow rhabdoms (1.5-2|im), whereas the crepuscular Australian butterfly, Melanitis leda, has 35-|im facets and 5-|im rhabdoms. A further consequence of this optical system is that the rhabdom tip is imaged onto the cornea (Fig. 17C), which means that one can sometimes see magnified versions in the cornea of the wave-guide mode phenomena that occur in the rhabdom.
What we have seen is that butterfly eyes behave as apposition eyes, because light entering a single facet is received by a single rhabdom.
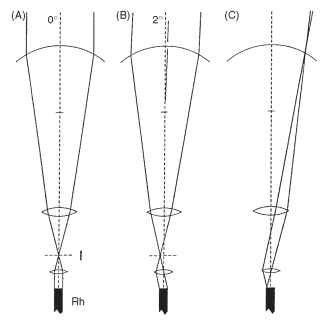
FIGURE 17 “Afocal” apposition in butterfly eyes. (A and B) Although each ommatidium acts independently, like an apposition eye, the optical elements function as telescopes with an internal image, as in superposition eyes (Fig. 13) . The wide beam of light reaching the cornea is reduced to “fit” the rhabdom (see text). (C) A consequence of this arrangement is that the rhabdom tip is imaged onto the cornea. I, image plane; Rh, rhabdom.
They are called afocal because light is not focused on the rhabdom tip as in most apposition eyes, but enters the rhabdom as a parallel beam. In their fundamental optical design, however, these ommatidia remain of the superposition type, constructed from two-lens telescopes. This makes it easy to understand how different lepidopteran groups managed to switch readily from the diurnal (apposition) version of the afo-cal eye to the nocturnal (superposition) version. To become nocturnal, the powers of the distal and proximal lenses must become more equal, the receptor layer moves to a deeper location, and gradually more and more facets contribute to the image. There are no blind intermediaries.
SIMPLE CORNEAL EYES IN INSECTS
Insect simple eyes, or ocelli, fall into two main groups: the larval eyes of holometabolous insects and the dorsal ocelli present in most winged adult insects. In both, the curved air/tissue cornea interface is the main refracting surface, although as in vertebrate eyes, a lens of some kind often augments the optical power of the system and aids in the formation of the image.
Larval Ocelli
In insects with a distinct larval stage, the ocelli are the only eyes the larvae possess. They vary greatly in size and complexity. The larvae of flies have no more than a small group of light-sensitive cells on either side of the head. Lepidopteran caterpillars, however, have ocelli with lenses and a structure resembling that of a single omma-tidium from a compound eye. In each ocellus in the Isia, seven receptors contribute to a two-tiered rhabdom containing the photo-pigment (Fig. 18A). There seems little possibility of spatial resolution
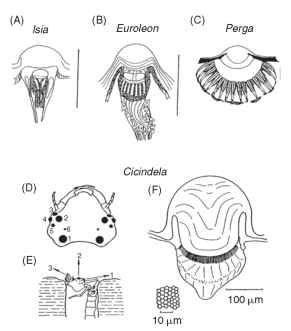
FIGURE 18 Simple eyes (ocelli) of increasing complexity in larval insects. (A) Lepidopteran, (B) Neuropteran, (C) Hymenopteran. Scale bars, 0.1 mm. (D-F) Large simple eyes of tiger beetle larvae (Cicindela) . They are used to spot prey (usually ants), which they ambush from the burrow. (D) Head with six pairs of eyes. (E) Larva in ambush position. (F) Largest ocellus showing corneal lens and retina. Inset: Tangential section of retina.
within each ocellus, but as it appears that the fields of view of the 12 ocelli do not overlap, they are capable of providing a 12-”pixel” sampling mosaic of the surroundings. These ocelli do, however, resolve color; three spectral types of receptor have been found in butterfly larval ocelli.
The ant lion Euroleon (Neuroptera) also has six ocelli on each side of the head, borne on a small turret (Fig. 18B). Unlike caterpillars, however, each has an extended retina of 40-50 receptors, giving interreceptor angles (Ace) of 5-10°. Although this resolution is not impressive, it is presumably enough to allow the animals to detect their prey, e.g., moving ants, at a distance of about 1 cm. Sawflies (Hymenoptera) have larvae with a single pair of ocelli, each with an in-focus retina covering a hemisphere (Fig. 18C). The rhabdoms in Perga are made up of the contributions from eight receptors (much as in an ordinary compound eye) and are spaced 20 |im apart, giving an interreceptor angle of 4-6°. These larvae are vegetarian, and it seems that the main function of the ocelli is to direct the larvae to their host plants. However, Perga larvae will also track moving objects with their head and defend themselves by spitting regurgitated sap.
The most impressive of all larval ocelli are found in tiger beetles (Cicindela). These have a lifestyle similar to that of ant lions, ambushing insect prey as they pass their burrows (Fig. 18D-18F). There are again six ocelli on each side of the head, but two are much larger than the others. The largest has a diameter of 0.2 mm and a retina containing 6350 receptors. The interreceptor angle is about 1.8°, comparable with or better than the resolution of the compound eyes of most adult insects. This raises the interesting question as to why the insects did not retain eyes like this into adult life.
Dorsal Ocelli of Adults
Adult insects that fly typically have three simple eyes on the top of their heads. These dorsal ocelli resemble larval ocelli in possessing a lens and (like sawfly larvae) an extended retina (Fig. 19), but they are not embryologically related to the larval eyes. Some dorsal ocelli have tapeta, and some a mobile iris. They each have a wide field of view of 150° or more and may have as many as 10,000 receptors. So far all this suggests that these are “good” eyes, like those of hunting spiders. However, they are profoundly out of focus, with the retina much too close to the lens. For example, in the blow fly Calliphora the receptors extend from 40 to 100 |im behind the lens, but the focus is at 120 |im.
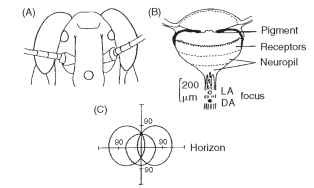
FIGURE 19 Dorsal ocelli of adult locust. (A) Positions of frontal and lateral ocelli on head. (B) Section of an ocellus, showing the different layers and the positions of the focus in light- and dark-adapted states. The focus is a long distance behind the receptor layers. (C) Fields of view of the three ocelli straddling the horizon.
What then are they for? Recent studies mainly support the idea that the ocelli are horizon detectors, involved in enabling an insect to make fast corrections for pitch and roll. The defocus then makes sense; high spatial frequency clutter such as leaves and branches will be removed, allowing the receptors to respond to changes in the overall distribution of light in the sky. The idea that these ocelli contribute to flight equilibrium is supported by the fact that the receptors converge massively onto a relatively few second-order neurons that project directly into the optomotor system.
