INTRODUCTION
Database modelling is a complex task that involves conceiving, understanding, structuring and describing real universes of discourse (UD) through the definition of schemata using abstraction processes and data models. Traditionally, three phases are identified in database design: conceptual, logical and physical design. The conceptual modelling phase represents the most abstract level since it is independent of any database management system (DBMS) and, consequently, it is very close to the user and allows him/her to collect almost completely the semantics of the real world to be modelled.
A conceptual schema, independent of the data formalism used, plays two main roles in the conceptual design phase: a semantic role, in which user requirements are gathered together and entities and relationships in a UD are documented, and a representational role that provides a framework that allows a mapping to the logical design of database development. Three topics are involved in the database conceptual modelling process: data modelling formalism, methodological approach, and CASE tool support. One of the most extended data modelling formalisms, extended entity relationship (EER) model, has proved to be a precise and comprehensive tool for representing data requirements in information systems development, mainly due to an adequate degree of abstraction of constructs that it includes. Although the original ER model was proposed by Chen (1976), many extensions and variations as well as different diagrammatic styles have been defined (Hull & King, 1987; McAllister, 1998; Peckhan & Maryanski, 1988).
In database conceptual analysis, one of the most difficult concepts to be modelled is the relationship concept, especially higher order relationships, as well as its associated cardinalities. Some text topics (Boman et al., 1997; Ullman & Widom, 2001) assume that any conceptual design can be addressed by considering only binary relationships since its aim is to create a computer-oriented model. We understand the advantages of this approach although we believe that it may produce certain loss of semantics (some biases are introduced in user requirements), and it forces to represent information in rather artificial and sometimes unnatural ways.
Concerning the logical design, the transformation process of conceptual schemata into relational schemata should be performed trying to preserve the semantics included in the conceptual schema completely; the final objective is to keep such semantics in the database itself and not in those applications that access to the database. Nevertheless, sometimes a certain loss of semantics is produced, for instance, foreign key and not null options in the relational model are not sufficient to control relationship cardinality constraints.
CONCEPTUAL MODEL REVISED
Central concepts of the ER conceptual model are entities and relationships; these constructs were introduced by Chen (1976) and have been incorporated in other conceptual models although with different names: class, type, and so forth, for entities and associations for relationships. Nevertheless, those concepts do not have a precise semantics, and, consequently, it is necessary to fix their meaning.
Although the entity concept is widely used and accepted, there is no agreement on one definition; for instance, Thalheim (2000) collects 12 different entity denotations. Although experts are not able to give a unique definition, the underlying concept is coincidental in all of them and its usage as design element does not suppose great disadvantages. An entity definition is not given here, just to highlight, according to Thalheim (2000), an entity is a representation abstraction with modeling purposes. Date (2004) adds that the represented concept is a distinguishable object, but we do not consider this feature as essential because it depends on the designer’s point of view.
The relationship concept is more confused; it is defined as an association among entities. This definition offers many interpretations; for instance, in several design methods there are some differences depending on the number of relations can participate in other relationships as in HERM (Thalheim, 2000) by means of association entities as in UML, OMG (2000), or by grouping as clusters a set of entities and relationships (Teorey, 1999). These differences occur because a relationship combines association features with representation features, and therefore, it might be considered a relationship (if association aspects are highlighted) or an entity (if representation aspects are emphasized).
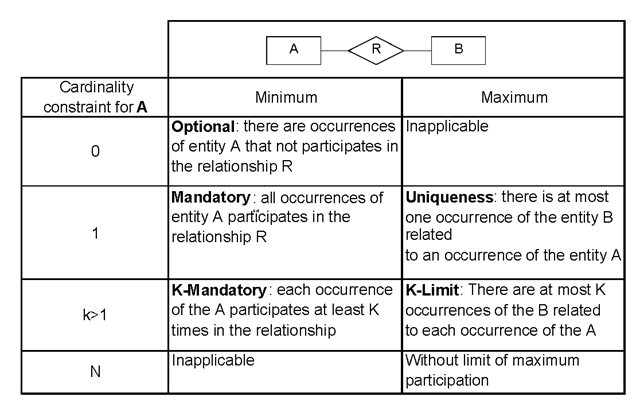
Cardinality constraint is one of the most important restrictions that can be established in a relationship, and in general, in a conceptual schema. Its functionality is to limit the number of entity occurrences associated in a relationship. Even though it is a simple concept, the definition of this constraint admits several variants.
Two main approaches are discussed: the Chen’s constraint that is an extension of the mapping constraint (a special case of cardinality constraint that considers only the maximum cardinality and that for binary relationships canbe 1:1, 1:N or N:M) (Chen, 1976); the Chen’s constraint has been adopted or extended in different data models and methodologies. On the other side, the MERISE approach (Tardieu, Rochfeld, & Coletti, 1983) incorporates the participation semantics. These two approaches meet each other when cardinality constraints for binary relationships are defined (excepting the natural differences in graphical notations). Both of them represent the same semantics in binary relationships although the way of expressing it is different. Table 1 summarises the semantics associated to cardinality constraint for the occurrences of A in the binary relationships R.
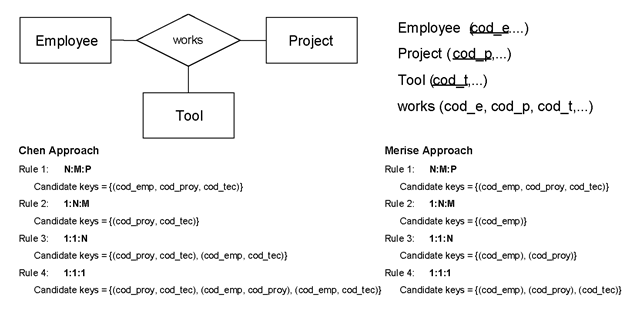
In nary relationships, the two approaches Chen and Merise, previously commented, do not represent the same semantics. Table 2 summarises the semantics associated to cardinality constraint for A in the n-ary relationship R depending of the approach.
TRANSFORMATION OF CONCEPTUAL SCHEMATA INTO RELATIONAL SCHEMATA
The main difficulty when transforming a conceptual schema into a relational schema is information preservation. Generally, to achieve a complete mapping between both models and keeping their inherent and semantic restrictions from conceptual model to relational model is quite complicated. Usually, restrictions that cannot be applied in the relational model must be reflected in the application in some different way, that is, outside the DBMS. In this way, there are several extensions to the relational model proposed by Codd (1970), Codd, (1979), Date, (2004) and Teorey (1999) that provide a more semantic model.
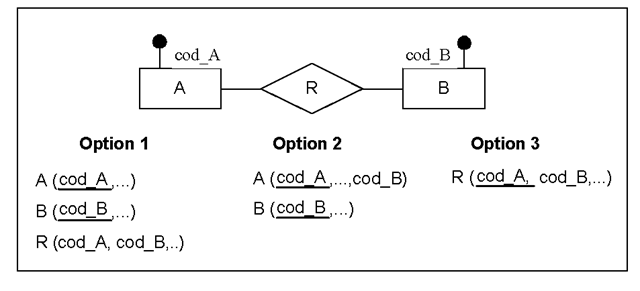
The principal transformation rules are described in most database text topics (Date, 2004; Elmasri & Navathe, 2003; Ramakrishnan & Gehrke, 2002), but these rules do not reflect the cardinality constraints transformation. In general, these rules can be classified for binary relationships transformation depending on the relations number that generated (Table 3). Option 1 makes a relation for each constructor, therefore the R relationship is transformed in a relation. Option 2 uses key propagation that is applied to a relationship which mapping constraint is 1:N or 1:1. Last, Option 3 only considers just one relation, to store the information of A, B and R constructors. This option is more restrictive than the others and only can be applied in a relationship which mapping constraint is 1:1.
Table 1. Cardinality constraint in binary relationship summary
Table 2. Cardinality constraint in n-ary relationship summary
| Chen Approach | Merise Approach | |||
| Cardinality constraint foA | Minimum | Maximum | Minimum | Maximum |
| 0 | Presence of unknown information | Inapplicable | Optional participation of the A ocurrences | Inapplicable |
| 1 | No constraint | For each (n-1) record there is one unique ocurrence related with one ocurrence of the entity A in the R | Mandatory participation of the A |
For each A ocurrence there are at most one ocurrences related in the R |
| k>1 | For each (n-1) record there are at least more than one ocurrences of the entity A related in the R | For each (n-1) record there is at most K ocurrences related with one ocurrence of the entity A in the R | For each A ocurrence there are at least more than K ocurrences related in the R | For each A ocurrence there are at most K ocurrences related in the R |
| N | Inapplicable | Without limit of maximum participation | Inapplicable | Without limit of maximum participation |
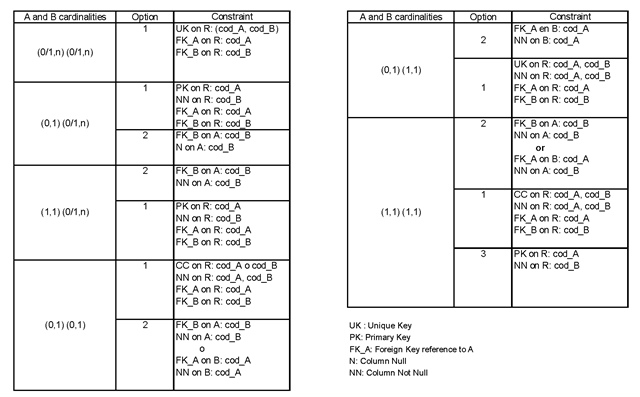
Table 4 explains when the different options explained in the Table 3 can be used depending on cardinality constraints (max. and min.) associated with the entities A and B and summarizes main transformation rules, indicated by options and relational constraints that must be included to add semantics. Relational constraints considered are: primary key (PK), unique key (UK), foreign key and the reference to relation X (FK_X), and optional attributes (N).
As we can see in Table 4, in most cases the minimum cardinality, the three first rows in the table, is not considered so its associated semantics is lost at the transformation.
When we transform n-ary relationships, we must take into account:
• the cardinality constraint approach used in the conceptual model;
• whether a relationship should be decomposed in minor grade relationships; and
• if the study cardinality constraint validation is needed.
Table 3. Binary relationship transformation options
The relationship decomposition and cardinality constraint validation study is a complex task that needs the interaction with domain experts to be solved. Therefore, transformations rules, on the whole, presented easy rules.
An example of different transformation rules with the Merise and Chen approaches for a ternary relationship is presented in Table 5. As it is shown in the table, rules only depend on mapping constraint.
In addition, the principal transformation rules for a ternary relationship, adopted for most design methodologies, appear independent of minimum cardinality constraints. This situation appears also in higher relationships.
Therefore, we can summarize that the cardinality constraint is one of the most important restrictions that can be established in a relationship, and in general, the semantics associated is loss in the transformation process to relational model.
CRITICAL ISSUES OF CARDINALITY CONSTRAINTS
After reviewing all conceptual constructs, it is needed to achieve a conceptual model as a tool that is able to reflect the situations that frequently appear in data modelling scenarios where it is required. The redefinition of the conceptual model, taking into account previous aspects as well as the development of a wider notation, are tasks to be dealt with.
The detection and specification of abstractions in an UD that lead to a correct and complete schema are critical problems that combine psychological and methodological aspects. There are many other aspects associated with the specification of constraints. Their identification and validation require more formal treatments. Identification can be faced up to with a lexical analysis of a problem description. Syntactic and semantic validation of relationships is a critical aspect of internal coherence with the UD. To obtain these properties, it is very important to:
• clarify the relationship definition;
• define formally relationship cardinality constraints and consider the two main approaches unification to higher order relationships;
• classify several approaches and provide conceptual model mappings; and
• provide a set of rules to validate relationships.
Table 4. Transformation rules summarised
On the other hand, another problem is how to preserve the cardinality constraint semantics in n-ary relationships for their implementation in a DBMS. There are some approaches, for example, in Balaban and Shoval (2002), an extension of the extended entity relationship (EER) model is made by including methods to control the semantics associated with Chen’s cardinalities. This approach adds a dynamic component to the model, but any database management system supports it. Camps (2002) makes a complete analysis of the transformation of maximum cardinality constraints into the relational model, considering Chen and Merise cardinalities for ternary relationships. They use equivalencies between cardinality constraints and functional dependencies, but this work does not concern to the transformation of minimum cardinalities problem. Finally, Cuadra et al. (2002) present the transformation of EER schemata into relational schemata using an extended relational model with active capabilities giving solutions to this problem.
Table 5. Transformation rules to apply an example
CONCLUSIONS
Conceptual models are well-known tools to achieve a good design of information systems. Nevertheless, the understanding and use of all constructs and constraints which are presented in these models are not an easy task, and sometimes it causes loss of motivation. Disagreements between main conceptual models, such as the confusion in the use of some of their constructs and some open problems in these models, are shown.
Another important topic treated in this chapter is the conceptual schema transformation into logical schema. Some solutions are presented in order to clarify the relationship construct and to extend the cardinality constraint concept, as well as several approaches to preserve the cardinality constraint semantics in n-ary relationships.
KEY TERMS
Cardinality Constraints: One constraint established in a relationship. It limits the number of entity occurrences that are associated in a relationship.
Chen Approach: One way to calculate cardinality constraints. It limits the participation of a combination of the other entity(ies) with an entity in the relationship.
Conceptual Models: Tools to achieve a good design of information systems. These tools are used to express information system requirements specification, and their principal characteristic is easy and intuitive use.
Entity: The basic element in a conceptual model that represents an abstraction with modelling purposes.
Logical Models: In a design methodology, tools to transform conceptual schemata into a schemata near to implementation. A well known principal model is the relational model.
Merise Approach: Another way to calculate cardinality constraints. It limits the participation of an entity in the relationship.
Relationship or Association: The basic element in one conceptual model. It is defined as an association among entities.
Semantics: Property that collect UD specifications and that should be preserved in the transformation schemata for all methodology phases.