A coordinate system is a way to locate places on a map, usually some type of grid laid over the map. Grid systems are a whole lot easier to use and more accurate than "take the old dirt road by the oak tree for two miles, then turn left at the rusted tractor, and you’ll be there when the road stops getting bumpy."
A simple coordinate system can consist of a vertical row of letters (A, B, C) on the left side of the map and a horizontal row of numbers (1, 2, 3) at the bottom of the map. If you want to tell someone where the town of Biggs Junction is (for example), you put your finger on the city and then move it in a straight line to the left until you hit the row of letters. Then put your finger on the city again, but this time move down until you reach the row of numbers. You now can say confidently that Biggs Junction is located at A12.
I call this the Battleship Grid System because it reminds me of the game where you call out coordinates to find your opponent’s hidden aircraft carriers, submarines, and destroyers. "B-3. You sank my battleship!"
A grid may be printed on the map or provide tick marks (representing the grid boundaries) at the map’s margins. Often maps have multiple coordinate systems so you can pick one that meets your needs or that you’re comfortable using. For example, USGS topographic maps have latitude and longitude, Universal Transverse Mercator (UTM), and township and range marks.
Most coordinate systems are based on x and y; where x is a horizontal value, and y is a vertical value. A location’s coordinates are expressed by drawing a straight line down to x and across to y. Mathematician Rene Descartes devised this system in the 1600s.
Letter-and-number coordinate systems are fine for highway maps, road atlases, and other simple maps where precise locations aren’t needed. However, if you want to focus on a precise location on a map, you need a more sophisticated grid system. That’s where coordinate systems such as latitude and longitude and UTM come in.
When you’re figuring out a location’s coordinates on a paper map, you have a fair amount of work to do, aligning the location with primary tick marks and then adding and subtracting to get the exact coordinate. With digital maps on a computer, that’s usually just a matter of moving the cursor over a location and watching with relief as the coordinates automatically appear. If you’re using a paper map, you can make life easier with free overlay grids and rulers from www.maptools.com. With these, you can print grids and rulers for different coordinate systems on clear transparency sheets.
Latitude/longitude
Latitude and longitude is the oldest map-coordinate system for plotting locations on the earth. The Roman scholar Ptolemy devised it almost 2,000 years ago. Ptolemy wrote about the difficulties of accurately representing the earth on a flat piece of paper and created latitude and longitude as a way of solving the problem. That’s pretty impressive for a time way before computers and satellites.
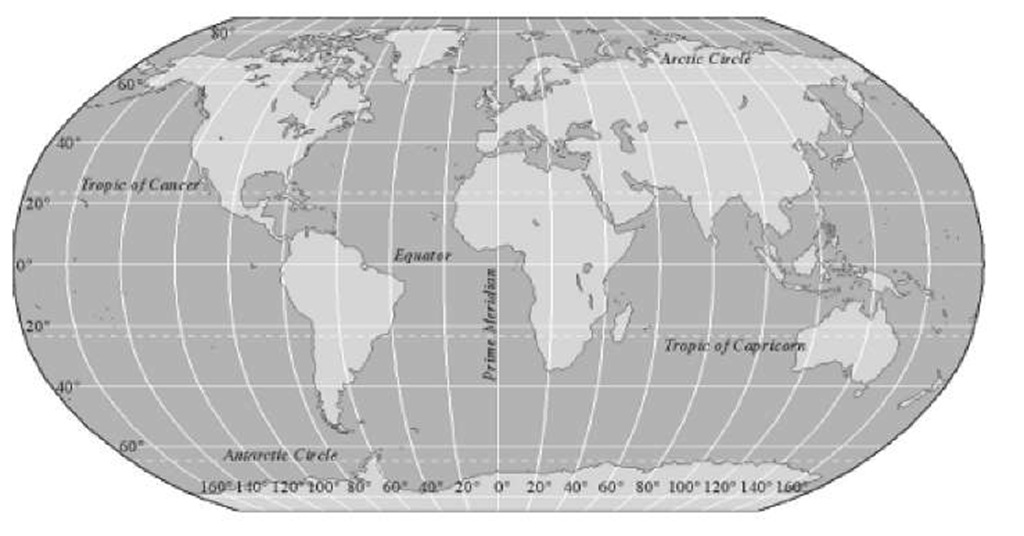
Latitude and longitude are based on a little math, but they’re not really complicated. Angles are measured in degrees, and they’re used for measuring circles and spheres. Spheres can be divided into 360 degrees; because the earth is basically a sphere, it can also be measured in degrees. This is the basis of latitude and longitude, which use imaginary degree lines to divide the surface of the earth (see Figure 2-5).
The equator is an imaginary circle around the earth; the circles are an equal distance from the north and south poles and perpendicular to the earth’s axis of rotation. The equator divides the earth into the Northern Hemisphere (everything north of the equator) and the Southern Hemisphere (everything south of the equator).
Figure 2-5:
Latitude and longitude are imaginary lines that provide a location reference.
Latitude
Latitude is the angular distance measured north and south of the equator (which represents 0 degrees of latitude).
I As you go north from the equator, the north latitude increases to 90 degrees when you arrive at the North Pole.
I As you go south of the equator, the south latitude increases to 90 degrees at the South Pole.
In the Northern Hemisphere, the latitude is always given in degrees north; in the southern hemisphere, it’s given in degrees south.
Longitude
Longitude works the same way as latitude, but the angular distances are measured east and west of the prime meridian (which marks the 0-degrees longitude line that passes through Greenwich, England, without even disturbing traffic).
When you travel east from the prime meridian, the longitude increases to 180 degrees.
As you go west from the prime meridian, longitude also increases to 180 degrees. (The place where the two 180-degree longitudes meet is known as the International Date Line.)
In the Eastern Hemisphere (which is east of the prime meridian to 180 degrees east), the longitude is given in degrees east.
In the Western Hemisphere (which is west of the prime meridian to 180 degrees west), longitude is expressed in degrees west.
One degree is actually a pretty big unit of measure. One degree of latitude or longitude is roughly equal to 70 miles.
Degrees are composed of smaller, fractional amounts that sound like you’re telling time.
Degree: A degree comprises 60 minutes.
One minute is about 1.2 miles.
Minute: A minute is composed of 60 seconds. One second is around .02 miles.
These measurement units are abbreviated with the following symbols:
Degree: ° Minute: ‘ ‘ Second:"
If you use minutes and seconds in conjunction with degrees, you can describe a very accurate location.
These distances are measured at the equator. At higher latitudes, the distance between longitude units decreases. The distance between latitude degrees is the same everywhere.
If you are using latitude and longitude to locate Dillon Falls on a map of the Deschutes River in Oregon, its coordinates are 43° 57′ 29.79" N 121° 24′ 34.73" W
Too much latitude
Latitude and longitude are pretty straightforward and logical if you think about it. Unfortunately, over the years, people have muddied things a bit by inventing different ways to represent latitude and longitude coordinates.
Latitude and longitude coordinates can be written as
Degrees, minutes, and seconds: This is the traditional way, with my example of Dillon Falls expressed as 43° 57′ 29.79" N 121° 24′ 34.73" W.
Degrees and decimal minutes: Seconds are dropped, and the decimal version of minutes is used along with degrees, so now the falls are at 43° 57.4965′ N 121° 24.5788′ W.
Decimal degrees: Minutes and seconds are both dropped, and only the decimal representation of degrees is used, which puts the falls at 43.9582750° N 121.4096490° W.
Remember: Although they look different, all these coordinate notations still point to the same location. The math is pretty straightforward if you want to convert the coordinates from one format to another. If you want to save time, point your Web browser to http://nris.state.mt. us/wis/location/latlong.asp where the friendly people at the Montana State Library have a handy conversion calculator online.
That means that Dillon Falls is 41 degrees, 57 minutes, and 29.76 seconds north of the equator 121 degrees, 24 minutes, 34.73 seconds west of the prime meridian
Universal Transverse Mercator (UTM)
Universal Transverse Mercator is a modern coordinate system developed in the 1940s. It’s similar to latitude and longitude, but it uses meters instead of degrees, minutes, and seconds. UTM coordinates are very accurate, and the system is pretty easy to use and understand.
Although the United States hasn’t moved to the metric system, the system is widely used by GPS receivers. UTM coordinates are much easier than latitude and longitude to plot on maps. The two key values to convert metric measurements are 1 meter = 3.28 feet = 1.09 yards.
For ballpark measurements, a meter is a bit over a yard.
1 kilometer = 1,000 meters = 3,280 feet = 1,094 yards = 0.62 miles.
For ballpark measurements, a kilometer is a bit more than half a mile.
Specialized coordinate systems
Here are a few other coordinate systems so you know what they are:
MGRS (Military Grid Reference System): A coordinate system used by the U.S. and NATO military forces. It’s an extension of the UTM system. It further divides the UTM zones into 100-kilometer squares labeled with the letters A-Z.
State Plane Coordinate System: A coordinate system used in the United States. Each state is divided into at least one State Plane zone. Similar to the UTM system, it uses feet instead of meters.
Proprietary grids: Anyone can invent a coordinate system for finding locations on a map.
Examples of proprietary systems are ZIP code, the Maidenhead Locator System (a grid system for amateur radio operators) and Thomas Brothers street guides.
Most coordinate systems try to make navigation and surveying more accurate and simpler.
GPS is sending less-used coordinate systems the way of the dinosaur because you can quickly and easily get precise location positions in either UTM coordinates or latitude and longitude with an inexpensive GPS receiver.
The UTM system is based on the simple A, B, C/1, 2, 3 coordinate system.
The world is divided into zones:
Sixty primary zones run north and south.
Numbers identify the zones that run north and south.
Twenty optional zones run east to west.
These zones indicate whether a coordinate is in the Northern or Southern Hemisphere.
Letters designate the east/west zones.
Often the letter is dropped from a UTM coordinate, and only the zone is used to make things simpler. For example, because most of Florida is in Zone 17 R, if you were plotting locations in that state, you could just use Zone 17 in your UTM coordinates. Figure 2-6 shows its UTM zone map.
To provide a precise location, UTM uses two units:
Easting: The distance in meters to the east from the start of a UTM zone line
The letter E follows Easting values.
Northing: The distance in meters from the equator
The letter N follows Northing values.
There’s no such thing as a Southing. Northing is used in the Southern Hemisphere to describe the distance away from the equator, even though a location is south of the Equator. (Is that weird, or what?)
Figure 2-6:
The UTM zone map for the world.
Continuing with my example of Dillon Falls, if you use UTM to locate the falls, the coordinates look like this:
10T 0627598E 4868251N
That means that the falls are in Zone 10T, which is 4,868,251 meters north of the equator and 627,598 meters east of where the zone line starts. (For those of you without a calculator in front of you, that’s about 3,025 miles north of the equator, and about 390 miles east of where the number 10 Zone line starts out in the Pacific Ocean.)
Township and Range
The Township and Range coordinate system has been used since the 1790s to survey public lands in the United States. Technically, the official name of this system is the Public Land Rectangular Survey (PLS), but in practical use, most people call it Township and Range.
This coordinate system was developed after the American Revolution as a way to survey and grant title to land that was newly acquired following the country’s independence. Thomas Jefferson helped develop the system, which was enacted under the Northwest Land Ordinance of 1785. Township and Range isn’t used in the eastern United States (or in a few other states) because land surveys in those states had been completed.
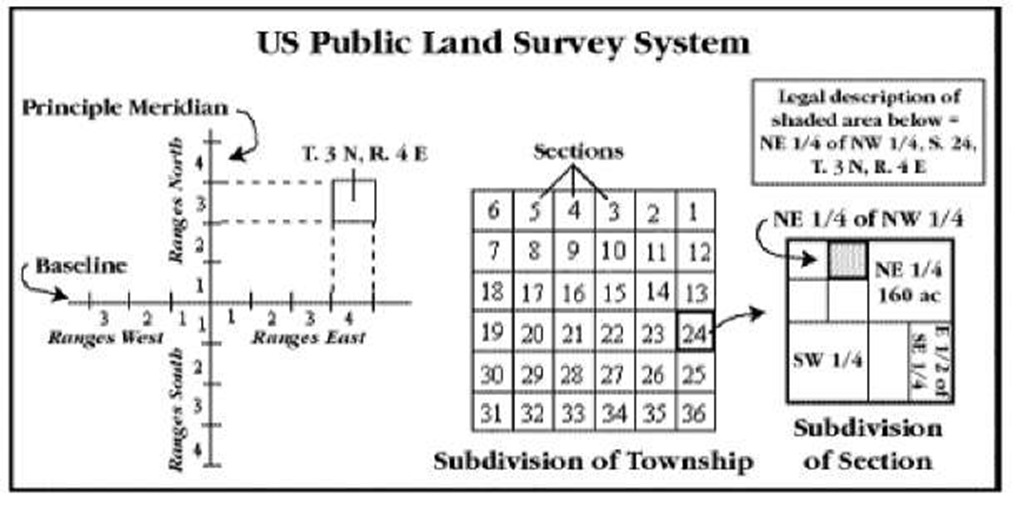
The system is based on the following components, which are shown in Figure 2-7:
Meridians and baselines. These lines are the foundation of the Township and Range system:
• Meridians are imaginary lines that run north to south.
• Baselines are lines that run east to west.
• An initial point is where a meridian and a baseline meet.
The California Bureau of Land Management has a nice online map of all the meridians and baselines at www.ca.blm.gov/pa/cadastral/ meridian.html.
Townships: Townships are the horizontal part of the coordinate system.
• Each township is six square miles in size.
• Townships are identified by whole numbers starting with 1.
• The first township at the intersection of a meridian and baseline is 1, the next township is 2, and so on.
• If a township is north of the baseline, it’s identified with an N; if it’s south of the baseline, it’s designated with an S. For example, the fifth township north of a meridian and baseline is T. 5 N.
Ranges: Ranges are the vertical part of the grid scale.
• Ranges are six miles wide.
• Ranges are numbered starting at the intersection of the meridian and the baseline.
• In addition to a number, a range is identified as being east or west of a meridian. For example, the third range west of the meridian and baseline is R. 3 W.
The intersection of a township and range (a 36-square mile parcel of land) also is also called a township. This bit of semantics shouldn’t have an effect on you using the coordinate system, but watch out for someone else doing this.
Like other coordinate systems, Township and Range uses smaller measurement units to identify a precise location. These units include
Sections: A 36-square-mile township is further divided into 36 one-mile squares called sections.
Sections are numbered 1-36. Number 1 starts in the top, right of the township, and the numbers sequentially snake back and forth across the section, ending at number 36 in the bottom-right corner.
Quarters: Sections are divided even further by slicing them into quarters.
• Quarters are identified by the part of the section they occupy, such as northwest, northeast, southwest, or southeast.
• You can further narrow the location with quarter quarters or quarter quarter-quarters.
Figure 2-7:
Elements that make up the Township and Range system.
Township and Range coordinates are a hodgepodge of abbreviations and numbers that lack the mathematical precision of latitude and longitude or UTM. For example, the Township and Range coordinates of Dillon Falls are
SE 1/4 of SW 1/4 of NE 1/4, Sect. 4, T. 19 S, R. 11 E, Willamette Meridian
To describe a location with this coordinate system, you start from the smallest chunk of land and then work your way up to larger chunks. Some people ignore this convention and reverse the order, skip the meridian, or use both halves and quarters. (Hey, it keeps life interesting. . . .)
Although scanned paper maps (such as USGS topographic maps) often show township and range information, most digital mapping software and GPS receivers don’t support township and range. This is good news because latitude and longitude and UTM are much easier to use.
Township and range information usually is omitted from digital maps because
The coordinate system is difficult to mathematically model.
Townships and sections may be oddly shaped because of previously granted lands, surveying errors, and adjustments for the curvature of the earth.
Peter Dana’s comprehensive Geographer’s Craft Web site has lots of good technical information on coordinate systems: