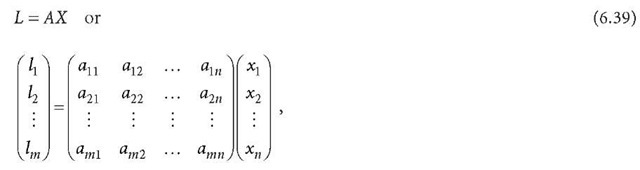
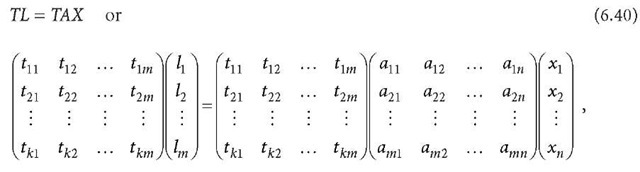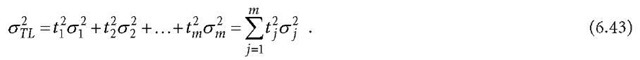For any linear equation system
a linear transformation can be defined as a multiplying operation of matrix T to Eq. 6.39, i.e.,
where T is called the linear transformation matrix and has a dimension of k x m. An inverse transformation of T is denoted by
An invertible linear transformation does not change the property (and solutions) of the original linear equations. This may be verified by multiplying
to Eq. 6.40. A non-invertible linear transformation is called a rank deficient (or not full rank) transformation.
The covariance matrix of L is denoted by cov(L) or QLL (cf. Sect. 6.2); then the co-variance of the transformed L (i.e., TL) can be obtained by covariance propagation theorem by (cf., e.g., Koch 1988)
where superscript T denotes the transpose of the transformation matrix.
If transformation matrix T is a vector (i.e., k =1) and L is an inhomogeneous and independent observable vector (i.e., covariance matrix
is a diagonal matrix with elements of
is the variance (
is called standard deviation) of the observable lj), then Eqs. 6.40 and 6.41 can be written as
Denoting cov(TL) as
one gets
Equation 6.43 is called the error propagation theorem. 6.5
