GPS satellites are orbiting around the Earth with time. GPS surveys are made mostly on the Earth. To describe the GPS observation (distance) as a function of the GPS orbit (satellite position) and the measuring position (station location), suitable coordinate and time systems have to be defined.
It is convenient to use the Earth-Centred Earth-Fixed (ECEF) coordinate system to describe the location of a station on the Earth’s surface. The ECEF coordinate system is a right-handed Cartesian system (x,y, z). Its origin and the Earth’s centre of mass coincide, while its z-axis and the mean rotational axis of the Earth coincide; the x-axis is pointing to the mean Greenwich meridian, while the y-axis is directed to complete a right-handed system (cf., Fig. 2.1). In other words, the z-axis is pointing to a mean pole of the Earth’s rotation. Such a mean pole, defined by international convention, is called the Conventional International Origin (CIO). Then the xy-plane is called mean equatorial plane, and the xz-plane is called mean zero-meridian.
Fig. 2.1.Earth-Centred Earth-Fixed coordinates
Fig. 2.2.
Cartesian and spherical coordinates
The ECEF coordinate system is also known as the Conventional Terrestrial System (CTS). The mean rotational axis and mean zero-meridian used here are necessary. The true rotational axis of the Earth changes its direction with respect to the Earth’s body all the time. If such a pole would be used to define a coordinate system, then the coordinates of the station would also change all the time. Because the surveying is made in our true world, so it is obvious that the polar motion has to be taken into account and will be discussed later.
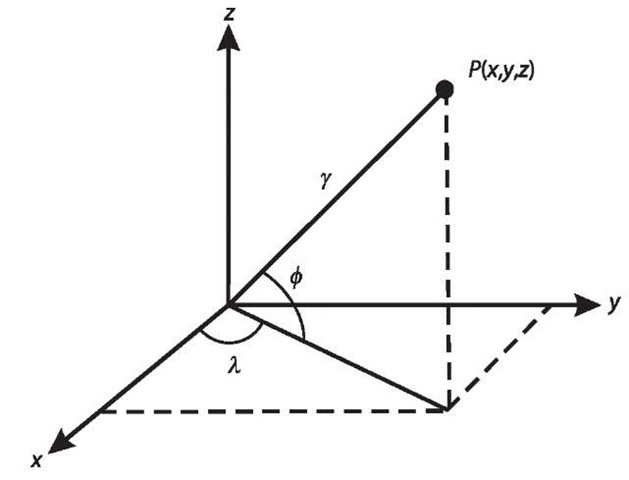
The ECEF coordinate system can, of course, be represented by a spherical coordinate system
where r is the radius of the point (x, y, z),
‘ are the geocentric latitude and longitude, respectively (cf., Fig. 2.2). X is counted eastward from the zero-meridian. The relationship between (x, y, z) and
is obvious:
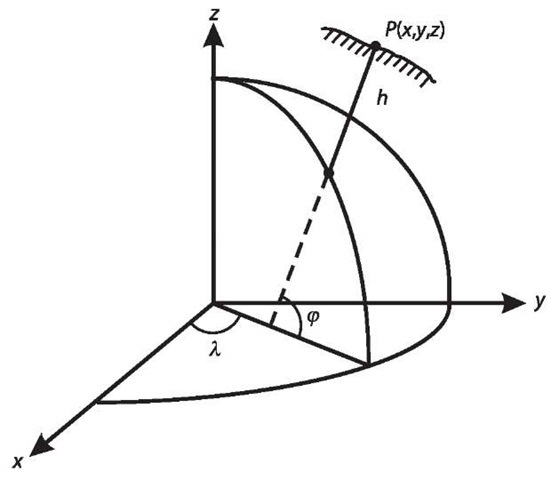
An ellipsoidal coordinate system
may be also defined based on the ECEF coordinates; however, geometrically, two additional parameters are needed to define the shape of the ellipsoid (cf., Fig. 2.3).
are geodetic latitude, longitude and height, respectively. The ellipsoidal surface is a rotational ellipse. The ellipsoidal system is also called the geodetic coordinate system. Geocentric longitude and geodetic longitude are identical. The two geometric parameters could be the semi-major radius (denote by a) and the semi-minor radius (denote by b) of the rotating ellipse, or the semi-major radius and the flattening (denote by f) of the ellipsoid. They are equivalent sets of parameters. The relationship between (x, y, z) and
is (cf., e.g., Torge 1991):
or
where
Fig. 2.3.
Ellipsoidal coordinate system
N is the radius of curvature in the prime vertical, and e is the first eccentricities. The geometric meaning of Nis shown in Fig. 2.4. In Eq. 2.3, the y and h have to be solved by iteration; however, the iteration process converges quickly, since h << N. The flattening and the first eccentricities are defined as:
In cases where
or h is very large, the iteration formulas of Eq. 2.3 could be instable. Alternatively, using (cf., Lelgemann 2002)
may lead to a stably iterated result of
are the lengths of
(cf., Fig. 2.4) respectively. h can be obtained by using
i.e.,
Fig. 2.4.
Radius of curvature in the prime vertical
The two geometric parameters used in the World Geodetic System 1984 (WGS-84) are (a = 6 378137 m, f = 1 / 298.2572236). In International Terrestrial Reference Frame 1996 (ITRF-96), the two parameters are (a = 6 378136.49 m, f = 1/298.25645). ITRF uses the International Earth Rotation Service (IERS) Conventions (cf., McCarthy 1996). In PZ-90 (Parameters of the Earth Year 1990) coordinate system of GLONASS, the two parameters are (a = 6 378 136 m, f = 1 /298.2578393).
The relation between the geocentric and geodetic latitude 0 and ymay be given by (cf., Eqs. 2.1 and 2.3):
