Map projections
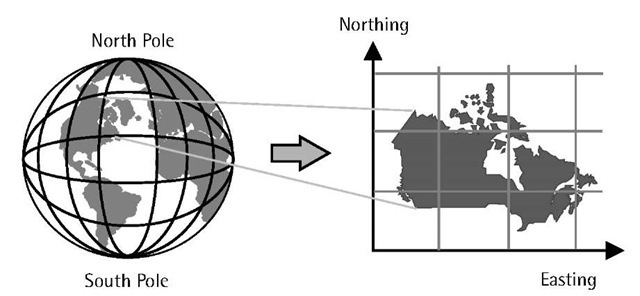
Map projection is defined, from the geometrical point of view, as the transformation of the physical features on the curved Earth’s surface onto a flat surface called a map (see Figure 4.6). However, it is defined, from the mathematical point of view, as the transformation of geodetic coordinates (f, l) obtained from, for example, GPS, into rectangular grid coordinates often called easting and northing. This is known as the direct map projection [2, 4].
Figure 4.6 Concept of map projection.
The inverse map projection involves the transformation of the grid coordinates into geodetic coordinates. Rectangular grid coordinates are widely used in practice, especially the Geomatics-related works. This is mainly because mathematical computations are performed easier on the mapping plane as compared with the reference surface (i.e., the ellipsoid).
Unfortunately, because of the difference between the ellipsoidal shape of the Earth and the flat projection surface, the projected features suffer from distortion [3]. In fact, this is similar to trying to flatten the peel of one-half of an orange; we will have to stretch portions and shrink others, which results in distorting the original shape of the peel. A number of projection types have been developed to minimize map distortions. In most of the GPS applications, the so-called conformal map projection is used [2]. With conformal map projection, the angles on the surface of the ellipsoid are preserved after being projected on the flat projection surface (i.e., the map). However, both the areas and the scales are distorted; remember that areas are either squeezed or stretched [9]. The most popular conformal map projections are transverse Mercator, universal transverse Mercator (UTM), and Lambert conformal conic projections.
It should be pointed out that not only the projection type should accompany the grid coordinates of a point, but also the reference system. This is because the geodetic coordinates of a particular point will vary from one reference system to another. For example, a particular point will have different pairs of UTM coordinates if the reference systems are different (e.g., NAD 27 and NAD 83).
Transverse Mercator projection
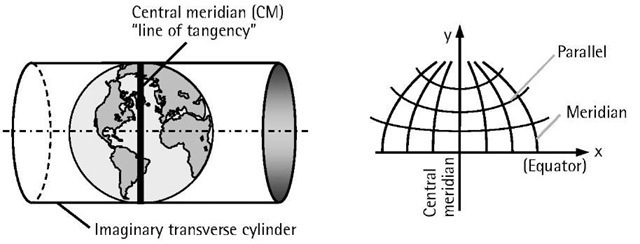
Transverse Mercator projection (also known as Gauss-Kruger projection) is a conformal map projection invented by Johann Lambert (Germany) in 1772 [9]. It is based on projecting the points on the ellipsoidal surface mathematically onto an imaginary transverse cylinder (i.e., its axis lies in the equatorial plane). The cylinder can be either a tangent to the ellipsoid along a meridian called the central meridian, or a secant cylinder (see Figure 4.7 for the case of tangent cylinder). In the latter case, two small complex curves at equal distance from the central meridian are produced.
Upon cutting and unfolding the imaginary cylinder, the required flat map (i.e., transverse Mercator projection) is produced. Again, it should be understood that the transverse cylinder is only an imaginary surface. As explained earlier, the projection is made mathematically through the transformation of the geodetic coordinates into the grid coordinates.
Figure 4.7 Transverse Mercator map projection.
In the case of a tangent cylinder, all features along the line of tangency, the central meridian, are mapped without distortion. This means that the scale, which is a measure of the amount of distortion, is true (equals one) along the central meridian. As we move away from the central meridian, the projected features will suffer from distortion. The farther we are from the central meridian, the greater the distortion. In fact, the scale factor increases symmetrically as we move away from the central meridian. This is why this projection is more suitable for areas that are long in the north-south direction.
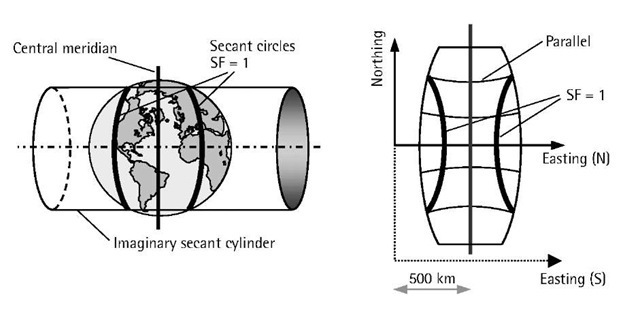
In the case of a secant cylinder, all features along the two small complex curves will be mapped without distortion (see Figure 4.8). The scale is true along the two small complex curves, not the central meridian. Similar to the tangent cylinder case, the distortion increases as we move away from the two small complex curves.
Universal transverse Mercator projection
The universal transverse Mercator (UTM) is a map projection that is based completely on the original transverse Mercator, with a secant cylinder (Figure 4.8). With UTM, however, the Earth (i.e., the ellipsoid) is divided into 60 zones of the same size; each zone has its own central meridian that is located at exactly the middle of the zone [9]. This means that each zone covers 6° of longitude, 3° on each side of the zone’s central meridian. Each zone is projected separately (i.e., the imaginary cylinder will be rotated around the Earth), which leads to a much smaller distortion compared with the original transverse Mercator projection.
Figure 4.8 UTM projection.
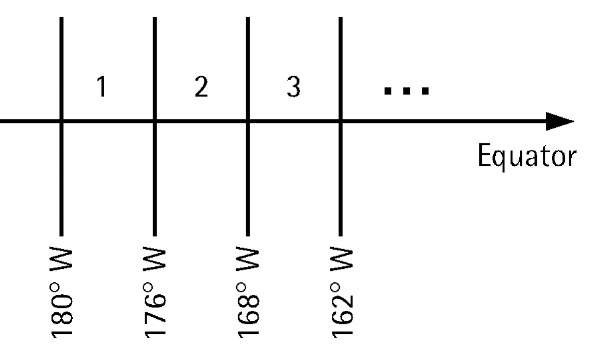
Each zone is assigned a number ranging from 1 to 60, starting from l = 180° W, and increases eastward (i.e., zone 1 starts at 180° W and ends at 174° W with its central meridian at 177° W); see Figure 4.9.
UTM utilizes a scale factor of 0.9996 along the zone’s central meridian (Figure 4.8). The reason for selecting this scale factor is to have a more uniformly distributed scale, with a minimum deviation from one, over the entire zone. For example, at the equator, the scale factor changes from 0.9996 at the central meridian to 1.00097 at the edge of the zone, while at midlatitude![]() the scale changes from 0.9996 at the central meridian to 1.00029 at the edge of the zone.
the scale changes from 0.9996 at the central meridian to 1.00029 at the edge of the zone.
Figure 4.9 UTM zoning.
This shows how the distortion is kept at a minimal level with UTM.
To avoid negative coordinates, the true origin of the grid coordinates (i.e., where the equator meets the central meridian of the zone) is shifted by introducing the so-called false northing and false easting (Figure 4.8). The false northing and false easting take different values, depending on whether we are in the northern or the southern hemisphere. For the northern hemisphere, the false northing and false easting are 0.0 km and 500 km, respectively, while for the southern hemisphere, they are 10,000 km, and 500 km, respectively.
A final point to be made here is that UTM is not suitable for projecting the polar regions. This is mainly due to the many zones to be involved when projecting a small polar area. Other projection types, such as the stereographic double projection, may be used (see Section 4.5.5).
Modified transverse Mercator projection
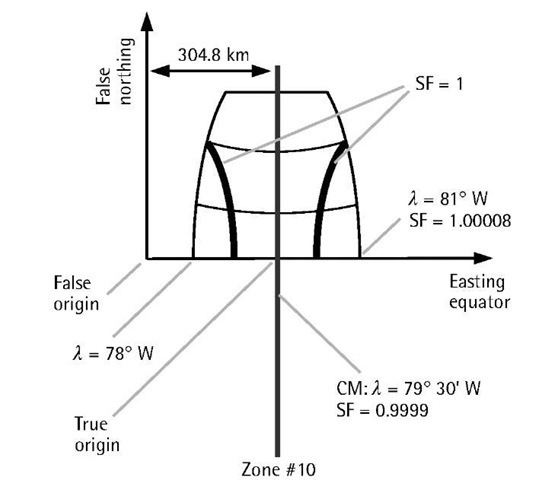
The modified transverse Mercator (MTM) projection is another projection that, similar to the UTM, is based completely on the original transverse Mercator, with a secant cylinder [9]. MTM is used in some Canadian provinces such as the province of Ontario. With MTM, a region is divided into zones of 3° of longitude each (i.e., 1.5° on each side of the zone’s central meridian). Similar to UTM, each zone is projected separately, which leads to a small distortion. In Canada, the first zone starts at some point just east of Newfoundland![]() and increases westward. Canada is covered by a total of 32 zones, while the province of Ontario is covered by 10 zones (zones 8 through 17). Figure 4.10 shows zone 10, where the city of Toronto is located.
and increases westward. Canada is covered by a total of 32 zones, while the province of Ontario is covered by 10 zones (zones 8 through 17). Figure 4.10 shows zone 10, where the city of Toronto is located.
MTM utilizes a scale factor of 0.9999 along the zone’s central meridian (Figure 4.10). This leads to even less distortion throughout the zone, as compared with the UTM. For example, at a latitude of![]() the scale factor changes from 0.9999 at the central meridian to 1.0000803 at the boundary of the zone. This shows how the scale variation and, consequently, the distortion are minimized with MTM [9]. This, however, has the disadvantage that the number of zones is doubled.
the scale factor changes from 0.9999 at the central meridian to 1.0000803 at the boundary of the zone. This shows how the scale variation and, consequently, the distortion are minimized with MTM [9]. This, however, has the disadvantage that the number of zones is doubled.
Similar to UTM, to avoid negative coordinates, the true origin of the grid coordinates is shifted by introducing the false northing and false easting. As Canada is completely located in the northern hemisphere, there is only one false northing and one false easting of 0.0m and 304,800m, respectively (see Figure 4.10).
Figure 4.10 MTM projection.
Lambert conical projection
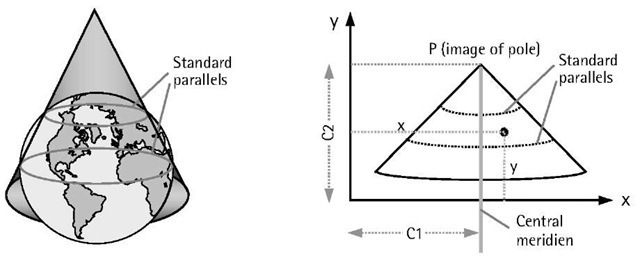
Lambert conical projection is a conformal map projection developed by Johann Lambert (Germany) in 1772 (the same year in which he developed the transverse Mercator projection). It is based on projecting the points on the ellipsoidal surface mathematically onto an imaginary cone [9]. The cone may either touch the ellipsoid along one of the parallels or intersect the ellipsoid along two parallels. The resulting parallels are called the standard parallels (i.e., one standard parallel is produced in the first case while two standard parallels are produced in the second case). Upon cutting and unfolding the imaginary cone, the required flat map is produced (Figure 4.11).
As with the case of the transverse Mercator projection, all features along the standard parallels are mapped without distortion. As we move away from the standard parallels, the projected features will suffer from distortion. This means that this projection is more suitable for areas that extend in the east-west direction.
Figure 4.11 Lambert conical projection.
This projection is designed so that all the parallels are projected as parts of concentric circles with the center at the apex of the cone, while all the meridians are projected as straight lines converging at the apex of the cone. In other words, the meridians will be the radii of concentric centers. A central meridian that nearly passes through the middle of the area to be mapped is selected to establish the direction of the grid north (i.e., the y-axis). To avoid negative coordinates, the origin of the grid coordinates is shifted by introducing two constants, C1 and C2 (see Figure 4.11). The values of C1, C2, and the latitude of the standard parallels are determined by the mapping authorities.
Stereographic double projection
The stereographic double projection is a map projection used in some parts of the world, including the Canadian province of New Brunswick. With this mapping projection, points on the reference ellipsoid are projected onto the projection plane through an intermediate surface: an imaginary sphere [9]. In other words, the projection is done in two steps, hence the name "double projection." First, features on the reference ellipsoid are conformally projected onto an imaginary sphere. Second, features on the sphere are conformally projected onto a tangent or a secant plane to produce the required map (Figure 4.12). The latter projection is known as stereographic projection.
Figure 4.12 Stereographic double projection.
There are three cases of stereographic projection to be obtained depending on the position of the projection plane relative to the sphere (i.e., the origin O). If the origin is selected at one of the poles of the sphere, the projection is called polar stereographic. However, if it is selected at some point on the equator of the sphere, the projection is called transverse or equatorial stereographic. The general case in which the origin is selected at an arbitrary point is called oblique stereographic. In the last case, the meridian passing through the map origin is projected as a straight line. All other meridians and parallels are projected as circles. In New Brunswick, a secant projection plane is used with an origin selected at f = 46° 30′ N and l = 66° 30′ W.
In the stereographic projection, a perspective point (P) is first selected to be diametrically opposite to the origin (O). If a secant projection plane is used, a point (A) on the surface of the sphere is projected by drawing a line (PA) and extending it outward to A’ on the projection plane (see Figure 4.12). Points inside the secant circle, such as point B, are projected inward. As discussed before, features along the secant circle are projected without distortion, while other features suffer from distortion. In New Brunswick, a scale factor of 0.999912 is selected at the origin. Similar to the previous three map projections, a false northing and a false easting are introduced to avoid negative coordinates.
Marine nautical charts
Marine nautical charts are maps used by mariners for navigation purposes. They contain information such as aids to navigation and hazards. Until recently, paper charts were the only source of information available to mariners. However, over a decade ago, the Electronic Chart Display and Information System (ECDIS) was introduced, revolutionizing the field of marine navigation.
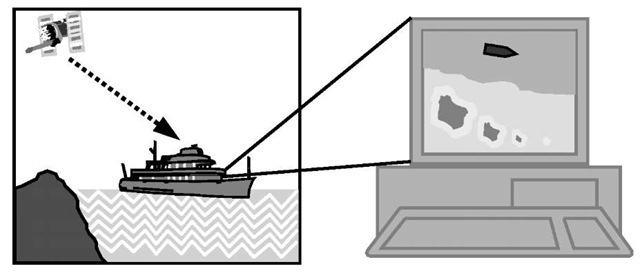
ECDIS is a computerized navigation system that integrates geographic information with navigation instrumentation [10]. It consists mainly of a computer processor and display, a digital database, and navigation sensors (see Figure 4.13). ECDIS is not only capable of displaying the navigation-related information in real time but also supporting other advanced functions [11]. For example, rout planning, rout monitoring, and automatic alarms, to name a few, are all supported by ECDIS. ECDIS and Radar/Automatic Radar Plotting Aid (ARPA) may be superimposed on a single display to provide a system that can be used for collision avoidance as well. The International Maritime Organization (IMO) adopted the performance standards for ECDIS in November 1995. The standards specify, among other things, that two independent positioning sources are required for ECDIS [10].
A number of hydrographic offices are currently involved in producing ECDIS databases by digitizing existing paper charts (i.e., converting paper charts into digital computer files). However, this has the disadvantage that the paper charts are generally based on local datums. This means that correct datum shifts must be considered to ensure consistency [11]. In addition, the paper charts in some areas were based on old survey methods, which are far less accurate than the required standards. A complete resur-vey of those areas might be required to overcome this problem.
Figure 4.13 Marine nautical chart system.
Local arbitrary mapping systems
When surveying small areas, it is often more appropriate to employ a user-defined local plane coordinate system. In this case, the curved Earth’s surface may be considered as a plane surface with a negligible amount of distortion. To establish a local coordinate system with GPS, a set of points with known coordinate values in both the WGS 84 and the local system must be available [5].
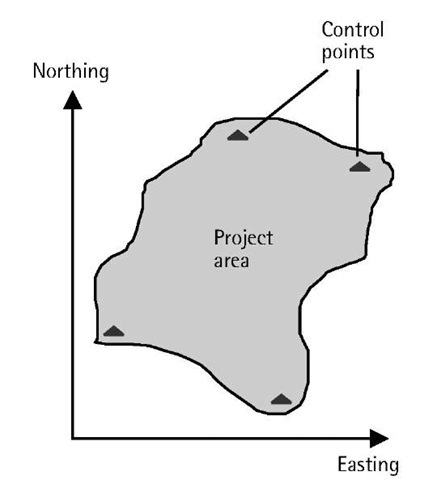
By comparing the coordinates of the common points (i.e., points with known coordinates in both the local system and the WGS 84 system), the transformation parameters may be obtained using the least squares technique. These transformation parameters will be used to transform all the new GPS-derived coordinates into the local coordinate system. It should be noted that the better the distribution of the common points, the better the solution (see Figure 4.14). The number of common points also plays an important role. The greater the number of common points, the better the solution [2].
Establishing a local coordinate system is usually done in either of two ways. One way is to supply the transformation parameters software (usually provided by the manufacturers of the GPS receivers) with the coordinates of the common points in both systems, if they are available.
Figure 4.14 Local arbitrary mapping system.
The software will then compute the transformation parameters, which once downloaded into the GPS data collector will be used to automatically transform all the new coordinates into the local coordinate system. Alternatively, if the coordinates of a set of points are known only in the local coordinate system, the user may occupy those points with the rover receiver to obtain their coordinates in the WGS 84 system. Real-time kinematic (RTK) GPS surveying is normally used for this purpose. This allows the determination of the transformation parameters while in the field.
Height systems
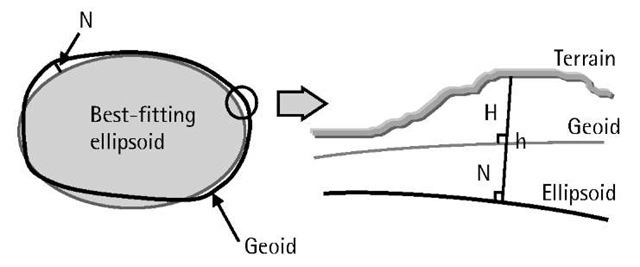
The height (or elevation) of a point is defined as the vertical distance from the vertical datum to the point (Figure 4.15). As stated in Section 4.1, the geoid is often selected to be the vertical datum [2]. The height of a point above the geoid is known as the orthometric height. It can be positive or negative depending on whether the point is located above or below the geoid. Because they are physically meaningful, orthometric heights are often needed in practice and are usually found plotted on topographic maps [2].
In some cases, such as the case ofGPS, the obtained heights are referred to the reference ellipsoid, not the geoid (Figure 4.15). Therefore, these heights are known as the ellipsoidal heights. An ellipsoidal height can also be positive or negative depending on whether the point is located above or below the surface of the reference ellipsoid. Unfortunately, ellipsoidal heights are purely geometrical and do not have any physical meaning. As such, the various Geomatics instruments (e.g., the total stations) cannot directly sense them.
The geoid-ellipsoid separation is known as the geoidal height or undulation (Figure 4.15). This distance can reach up to about 100m, and it can be positive or negative depending on whether the geoid is above or below the reference ellipsoid at a particular point [12]. Accurate information about the geoidal height leads to the determination of the orthometric height through the ellipsoidal height, and vice versa. Geoid models that describe the geoidal heights for the whole world have been developed.
Figure 4.15 Height systems.
Unfortunately, these models do not have consistent accuracy levels everywhere, mainly because of the lack of local gravity data and the associated height information in some parts of the world [12]. Many GPS receivers and software packages have built-in geoid models for automatic conversion between orthometric and ellipsoidal heights. However, care must be taken when applying them, as they are usually low-accuracy models.