The previous topic showed that centimeter-level positioning accuracy could be achieved with the carrier-phase observables in the relative positioning mode. A prerequisite to this, however, is the successful determination of the initial integer ambiguity parameters (in fact, the integer double-difference ambiguity parameters). This process is commonly known as ambiguity resolution. Resolving the ambiguity parameters correctly is equivalent to having very precise ranges to the satellites, which leads to high-accuracy positioning [1].
The ambiguity parameters are initially determined as part of the least-squares, or Kalman filtering, solution [2, 3]. Unfortunately, however, neither method can directly determine the integer numbers of the ambiguity parameters. What can be obtained are the real-valued numbers along with their uncertainty parameters (so-called covariance matrix) only. These real-valued numbers are in fact difficult to separate from the baseline solution [4]. As such, since we know in advance that the ambiguity parameters are integer numbers, it becomes clear that further analysis is required.
Traditionally, high-precision GPS relative positioning with carrier-phase observables was carried out using long observational time spans (typically a few hours). This allows for the receiver-satellite geometry to change considerably, which helps in separating the ambiguity parameters from the baseline solution. As such, even though the least-squares solution would contain real-valued numbers for the ambiguity parameters, they were very close to integer values. Consequently, the correct integer values were simply obtained by rounding off the real-valued numbers to the nearest integers [4]. Another least-squares adjustment was then to be carried out, considering the integer-valued ambiguity parameters as known values while the baseline components are unknowns. It is clear that, although this method is capable of determining the correct integer values of the ambiguity parameters, it is time-consuming. As such, the use of this method is currently limited to long baselines in the static mode.
Various methods have been developed to overcome the limitation of the previous method (i.e., the use of long observational time spans). One such method is to use a known baseline (i.e., the coordinates of its end points are accurately known), which might be available within the project area. The ambiguity parameters are determined by simply occupying the two end points of the known baseline with the base and the rover receivers for a short period of time. This process is commonly known as receiver initialization. Following receiver initialization, the rover receiver can move to the points to be surveyed. With this method, the receiver uses the ambiguity parameters determined during the initialization to solve for the coordinates of the new points.The initial integer number of cycles (the ambiguity parameter) remains constant over time, even if the receiver is in motion, as long as no cycle slips have occurred. In other words, it is necessary that the receivers be kept "on" all the time and that at least four common satellites are tracked at any moment. An alternative initialization method is known as the antenna swap method, which can be used when no known baseline is available within the project area. This method, which was introduced by Dr. Ben Remondi in 1986, is based on exchanging the antennas between the base and the rover while tracking at least four satellites. More details on this method are given later. Both the known baseline and the antenna swap methods are more suitable for kinematic positioning in the postprocessing mode.
These three methods are suitable for non-real-time applications, with which the data are collected in the field and then postprocessed at later times. RTK positioning, however, requires that the integer ambiguity parameters be determined while the receiver is in motion, or on the fly [5]. Resolving the ambiguities on the fly, often called on-the-fly ambiguity resolution, is different from the ambiguity-resolution techniques mentioned earlier in the sense that the initialization is performed in the field using very short observational time spans. Due to the high altitudes of the GPS satellites, the receiver-satellite geometry changes very slowly over time. As such, a short time span of data causes some difficulties in resolving the ambiguities. Fortunately, a more advanced technique has been developed to overcome this limitation; this technique is discussed later.
Antenna swap method
The antenna swap is a method used for a fast and reliable determination of the initial ambiguity parameters (i.e., initialization) in the postprocessing mode [6]. This method is used mainly when single-frequency receivers are used for kinematic surveying, although it can be used with dual frequency as well.
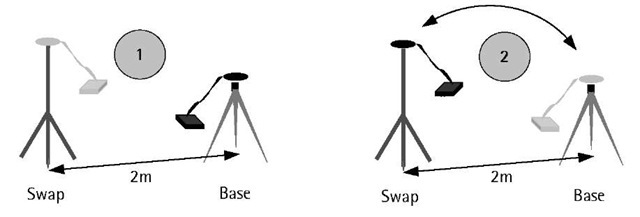
The initialization procedures with the antenna swap method start by setting up the reference (base) receiver over the known point while setting up the rover within a few meters from it (Figure 6.1). About 1-minute simultaneous GPS data is then to be collected at both receivers. Usually, a data rate as high as 1 or 2 seconds is used. Once the data is collected, the two antennas (with the two GPS receivers connected to them) are exchanged (see Figure 6.1). This is done without changing the original antenna heights. Care must be taken to keep tracking to a minimum of four, preferably five, common satellites. With this new setup, another simultaneous 1-minute GPS data, at the previous rate, is collected by both receivers. After this step, the receivers are returned to their original setup, which ends the initialization procedures.
Figure 6.1 Antenna swap method.
Once the initialization is performed, the base receiver must be kept stationary over the known point while the rover moves between the points to be surveyed, as discussed before in the kinematic method. After finishing the fieldwork, the data is downloaded into the PC processing software, which will first use the initialization data to determine the initial ambiguity parameters. Once determined, the software will use these parameters to determine the coordinates of the survey points at centimeter-level accuracy. It should be pointed out that a shorter observational time span would be enough for the receiver initialization.
On-the-fly ambiguity resolution
On-the-fly (OTF) ambiguity resolution is an advanced technique developed recently to determine the initial integer ambiguity parameters without static initialization (i.e., while the rover receiver is moving). This technique may be applied with either single- or dual-frequency data. However, resolving the ambiguities is faster and more reliable with dual-frequency data. It is used mainly for, but not restricted to, real-time kinematic operations.
Several OTF techniques have been developed over the past several years. Only one method is summarized here [4]. The base and rover measurements are combined in the double differenced mode and an initial adjustment by, for example, the least squares or Kalman filtering technique, is then performed. The outcome of this initial adjustment is an initial rover position along with estimates (real values) for the ambiguity parameters and their uncertainty values, or the covariance matrix.
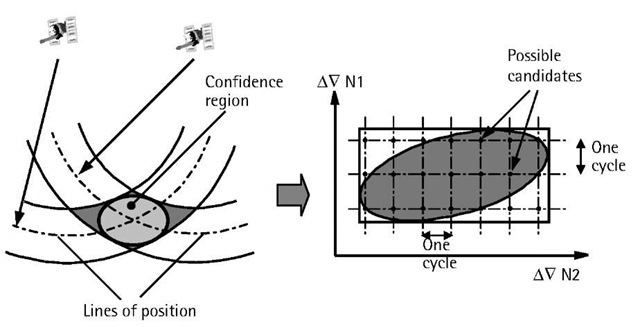
The covariance matrix can be represented geometrically to form a region, known as the confidence region, around the estimated real-value ambiguity parameters [4]. The size of such a confidence region depends on the size of the uncertainty parameters of the ambiguities as well as the used probability level. The larger the uncertainty values and/or the probability level, the larger the size of the confidence region. The confidence region takes the shape of an ellipse if the number of the estimated parameters is two, and an ellipsoid if it is three. If the number of estimated parameters is more than three, which is the case if the number of satellites is more than four, a confidence region of a hyperellipsoid is obtained.
Generally, a confidence region of a hyperellipsoid is formed around the estimated real-valued ambiguity parameters. Such a hyperellipsoid contains the likely integer ambiguity parameters at a certain probability level. For example, if a probability value of 99% is used to scale the hyperellipsoid, it means that there is a 99% chance that the true integer ambiguity parameters are located inside that hyperellipsoid. Since we know in advance that the ambiguity parameters must be integer numbers, we may draw (mathematically) gridlines that intersect at integer values inside the hyperellipsoid. If the grid spacing is selected to be equal to one carrier cycle, then the likely integer ambiguity parameters would be represented by one of the points of intersection inside the hyperellipsoid. Figure 6.2 simplifies this, using a 2-D case as an example. The hyperellipsoid is then used for searching the likely integer values for ambiguity parameters (i.e., all the points inside the confidence region with integer values). Based on statistical evaluation, only one point is selected as the most likely candidate for the integer ambiguity parameters. Once the ambiguities are correctly resolved, a final adjustment is performed to obtain the rover coordinates at centimeter-level accuracy. It should be pointed out that the OTF technique, although designed mainly for resolving the ambiguity parameters in real time, could also be used in the non-realtime mode.
Figure 6.2 OTF ambiguity resolution.