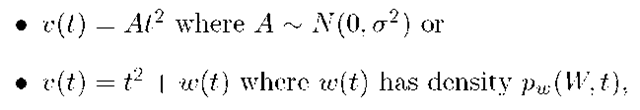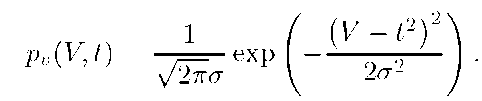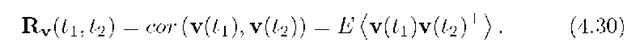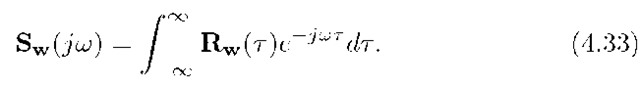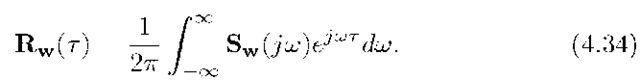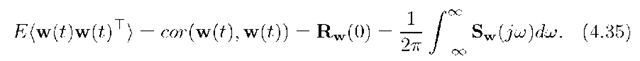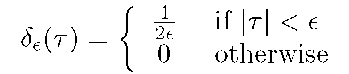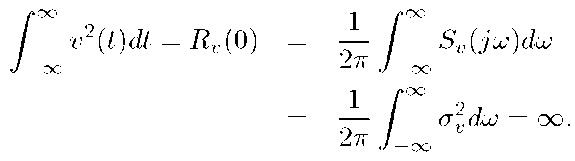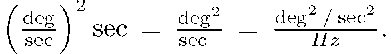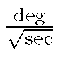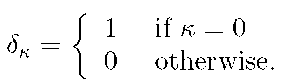In Depth Tutorials and Information

Stochastic Processes (GPS)

A stochastic process is a family of random variables indexed by a parameter for continuous-time stochastic processes orfor discrete-time stochastic sequences.

For a deterministic signal such asthe value of x is determined by the value of t. Once t is known, the value of x(t) is known. There is no element of chance. Alternatively, signals such as

are stochastic processes. In fact, in the above example,is also a stochastic process. For a stochastic processthe parameter t determines the distribution and statistics of the random variable v, but t does not determine the value ofinstead, given two timeswe have two distinct random variablesThe distributions for andmay be the same or distinct, depending on whether or not the stochastic process is stationary.

Example 4.11 Let

the density for v is

At each time,is a new Gaussian random variable with zero mean and varianceAt each time,is a new Gaussian random variable with meanand variance

Statistics and Statistical Properties

The statistical quantities defined previously for random variables become slightly more complicated when applied to stochastic processes, as they may depend on the parameter t or k. For continuous-time processes, the definitions are listed below. Note that these definitions are equally valid whether the parameter t represents a continuous or a discrete-time variable. The cross correlation function between two random processes is defined mby

The autocorrelation function of a random processes is defined by

The autocorrelation function quantifies the similarity of the random process to itself at two different times.

The cross covariance function between two random processes is defined by

The autocovariance function of a random processes is defined by

The above definitions will be critically important in the analysis of subsequent topics. For example, the Kalman filter will propagate certain error covariance matrices through time as a means to quantify the relative accuracy of various pieces of information that are to be combined.

There are two forms of stationary random processes that will be used in this text.

Definition 4.1 The random process w(t) is stationary if its distribution is independent of time

If a random process is stationary, then its expected value will be time invariant and both its autocorrelation function and its autocovariance function will only depend on the time difference

Often this strict sense of stationarity is too restrictive. A relaxed sense of stationarity is as follows.

Definition 4.2 The random process w(t) is wide sense stationary (WSS) if the mean and variance of the process are independent of time.

Since a Gaussian random process is completely defined by its first two moments, a Gaussian process that is wide sense stationary is also stationary. A wide sense stationary process must have a constant mean, and its correlation and covariance can only depend on the time difference between the occurrence of the two random variables, i.e.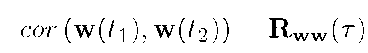

where

The Power Spectral Density (PSD) of a WSS random process w(t) is the Fourier transform of the autocorrelation function:

For real random variables, the power spectrum can be shown to be real and even.

If the PSD of a WSS random signal is known, then the correlation function can be calculated as the inverse Fourier transform of the PSD,

In particular, the average power of w(t) can be calculated as

White and Colored Noise

One stochastic process that is particularly useful for modeling purposes is white noise. The adjective ‘white’ indicates that this particular type of noise has constant power at all frequencies. Any process that does not have equal power per frequency interval will be referred to as colored. Because power distribution per frequency interval is the distinguishing factor, for both continuous-time and discrete-time white noise, our discussion will start from the PSD.

Continuous-time White Noise

A scalar continuous-time random process v(t) is referred to as a white noise process if its PSD is constant:

Then by eqn. (4.34), the autocorrelation function is

and

whereis the Dirac delta function:

and

which has units ofAn implication of eqn. (4.36) is that Nevertheless, problem assumptions will often state the fact thatis a zero mean, continuous-time, white noise process with

The fact that the spectral density is a constant function highlights the fact that continuous-time white noise processes are not realizable. All continuous-time white noise processes have infinite power, as demonstrated by eqn. (4.35):

Nonetheless, the white noise model is convenient for situations where the noise spectral density is constant over a frequency range significantly larger that the bandwidth of interest in a particular application.

A white noise process can have any probability distribution; however, the Gaussian distribution is often assumed. A key reason is the central limit theorem. If the analyst carefully constructs a model accounting for all known or predictable effects, then the remaining stochastic signals can often be accurately modeled as the output of a linear system that is driven by a Gaussian white noise input. This technique will be discussed in Section 4.5. In this topic, the notationwill sometimes be used to describe a continuous-time, Gaussion, white-noise processIn this case,is interpreted as the PSD, not the variance.

Reasoning through the units of the symboloften causes confusion. This can be considered from two perspectives. First, from the PSD perspective,represents the power per unit frequency interval. Therefore, the units ofare the units of v squared divided by the unit of frequency Hz. Second, from the perspective of correlation, .has the units of squared and the Dirac delta functionhas units oftherefore,has dimensions corresponding to the square of the units of v times sec. For example, if v is an angular rate inthenhas dimensions