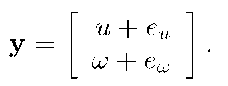Navigation system analysis, and portions of the implementation, involve linearization of a system about a nominal trajectory. This section explains the linearization process.
Let the state space model for a system with input u and output y be described by
Assume that for a nominal input
a nominal state trajectory
is known which satisfies
Define the error state vector as
Then,
We can approximate f (x, u) using a Taylor series expansion to yield
where
The resultant perturbation to the system output
is
where
By dropping the higher-order terms (h.o.t’s), eqns. (3.32) and (3.33) provide the time-varying linearization of the nonlinear system: 
which is accurate near the nominal trajectory (i.e., for small
and 
Applications of eqns. (3.34) and (3.35) are common in navigation applications. For example, the GPS range equations include the distance from the satellite broadcast antenna effective position to the receiver antenna effective position. When the satellite position is known and the objective is to estimate the receiver location, the GPS measurement is nonlinear with the generic form of eqn. (3.31), but frequently solved via linearization.The following example illustrates the basic state space linearization process.
Example 3.9 Assume that there is a true system that follows the kinematic equation
and 
For this system, the variables [n, e] defined the position vector, ^ is the yaw angle of the vehicle relative to north,, u is the body frame forward velocity, and
is the yaw rate. Also, assume that two sensors are available that provide measurements modeled as
A very simple dead-reckoning navigation system can be designed by integration of
from some initial
where
The resulting dead-reckoning system state,
will be used as the reference trajectory for the linearization process. The navigation system equation can be simplified as follows:
The first order (i.e., linearized) dynamics of the error between the actual and navigation states are
where
To derive this linearized model, the function f in eqn. (3.36) is expanded using Taylor series. Then eqn. (3.37) is subtracted from the Taylor series expansion of eqn.. (3.36) to yield eqn. (3.38).A
Error state dynamic equations enable quantitative analysis of the error state itself. Later, the linearized error state equations will be used in the design of Kalman filters to estimate the error state.
