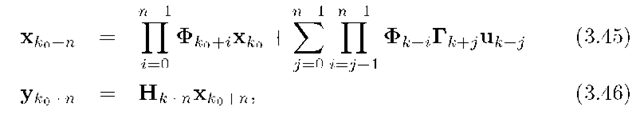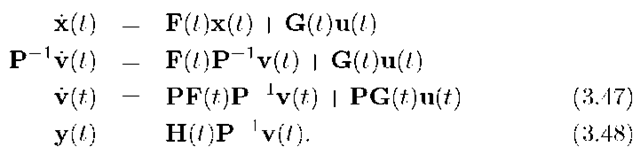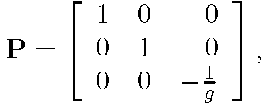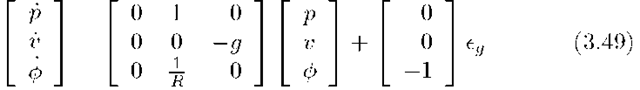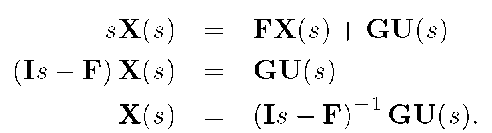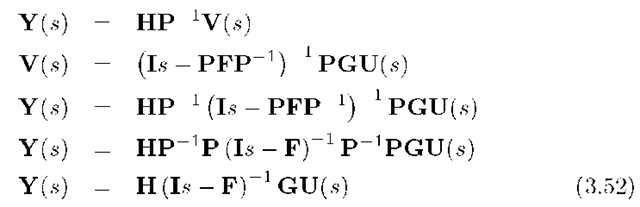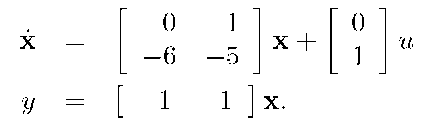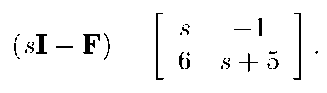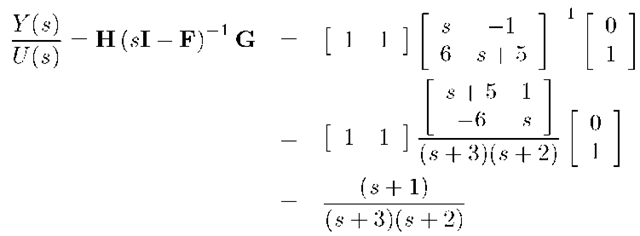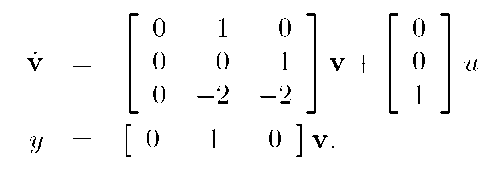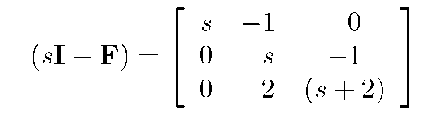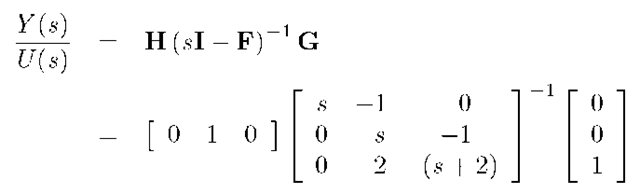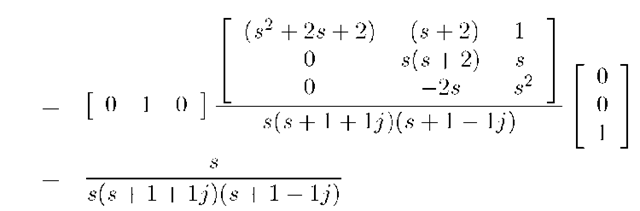The previous sections have casually referred to the state of a system. The following definition formalizes this concept.
Definition 3.1 The state of a dynamic system is a set of real variables such that knowledge of these variables at time to together with knowledge of the system input for
is sufficient to determine the system response for all
The definition of state for a discrete-time system is exactly the same with t replaced by k.
If the state variables are independent and organized as a vector, i.e., 
then x is the state vector and n is the order of the state space model.
The concept of state can be thought of as an extension of the idea of initial conditions. It is well understood that the complete solution of an nth order differential equation requires specification on n initial conditions. Also, as demonstrated in Section 3.1.3, the state space representation for an n-th order ordinary differential equation entails n state variables with one first-order differential equation for each state variable.
Sections 3.1.3 and 3.4 present the continuous and discrete-time state space models for time-invariant linear systems. In general, the coefficient matrices in these models can be time-varying. The general time-varying linear models are
and
The solution to eqn. (3.43) is involved and important in its own right, so it is discussed in Section 3.5.3. By direct iteration, it is straightforward to show that the solution to eqn. (3.44) is
which shows that knowledge of
completely specifies the system state and output for all
In eqn. (3.45), the order of the matrix product is important and is interpreted as
Similarity Transformation
Note that Definition 3.1 defines an equivalent class of state vectors of the same dimension. If the set of variables in
satisfies the definition of state, then so does
for any non-singular matrix P. This is true, since knowledge of v allows determination of x according to
therefore, v also satisfies the definition of the system state. The different representations of the state correspond to different scalings of the state variables or different selection of the (not necessarily orthogonal) basis vectors for the state space.
If the state space model corresponding to x is described by eqn. (3.43) and P is a constant matrix, then the state space representation for the state vector v is given in eqns. (3.47-3.48):
For specific types of analysis or for unit conversion, it may be convenient to find a nonsingular linear transformation of the original system state which simplifies the subsequent analysis. The use of similarity transformations for discrete-time systems is identical.
Example 3.10 Example 3.6 presented a state space model for a single channel of the error dynamics of the INS with state vector
An alternative state vector definition is
where
represents error in the computed orientation of the platform frame with respect to the navigation frame. Using the similarity transform
with
Exercise 3.4 asks the reader to confirm that an equivalent state space model is
with
The state space model of eqn. (3.49) is derived from first principles in Exercise 3.12. A
For important applications of the similarity transform, e.g., see Sections 3.6.2-3.6.3.
State Space to Transfer Function
Sections 3.1.3 and 3.4 presented a specific state space representation referred to as the controllable canonical form. This state space format has the advantage that it is easy to compute the associated transfer function and that it is straightforward to determine a state feedback control law, but may not be the model format that results from derivation of a system model based on physical principles. The previous section showed that there are an infinite number of equivalent state space model representations. This section describes how to find the associated transfer function when the available state space model is not in controllable canonical form. Only continuous-time systems are discussed. The analysis is similar for discrete-time systems.
If a time-invariant system is described as
then, assuming that all initial conditions are zero, Laplace transforming both sides results in
When
then by Laplace transform
and
To show that all equivalent state space representations have the same input output response, consider the transfer function corresponding to eqns. (3.47) and (3.48):
where we have used the fact that
which can be demonstrated by direct multiplication.
In relation to the previous analysisof this section it is useful to note the following facts. The quantity
represents a matrix of transfer functions. Before any pole-zero cancelations, the denominator of each transfer function is the polynomial
which is the determinant of
The system poles are the solutions to the equation
The eigenvalues of F are the solutions of
Therefore, before pole-zero cancelations, the eigenvalues of F and the poles of the transfer function from
are identical.
Example 3.11 Consider the state space system
The eigenvalues of F are the roots of
where
Therefore,
which shows that the eigenvalues are -2 and -3.
The transfer function from u to y is computed as
which has a zero at s = — 1 and poles at s = —2, — 3. Example 3.12 Consider the state space system
The eigenvalues are
which yields the following equation for the eigenvalues
The transfer function from u to y is computed as follows:
which has a finite zero at s = 0 and n = 3 poles at
Engineers and analysts should be extremely careful with pole-zero cancelations. In particular, a pole should never be canceled if it is in the right-half complex-plane and only with extreme caution if it is on the
of the complex plane. When a pole-zero cancelation occurs it only cancels for a specific transfer function. The order of that transfer function decreases, but the order of the state space representation remains n. The affect of the ‘canceled’ pole will still appear in other transfer functions and in the transient response.
