State Estimation (GPS) Part 2

Estimator Design by Pole Placement

This section discusses estimator design by pole placement (i.e., Ackerman’s method) for two reasons.Second, understanding of the concepts of this section will aid the understand of the results derived in Section 3.6.3.

Section 3.1.3 derived the controllable canonical form state space representation for the strictly proper transfer function in eqn. (3.6). For observer design by pole placement, it is also useful to define the observable canonical form. In discrete-time, the observable canonical form, state space representation is

where

andThe observable canonical form will be convenient for selection of the observer gain matrix, assuming that we have method for transforming an arbitrary state space representation to observable canonical form.

The observer gain matrix design process has three steps. First, we find a similarity transformfrom the original state space representation

to observable canonical form where andSecond, we select an observer gain vectorusing pole placement for the system in observable canonical form. Third, we use the equationto transform the observer gainback to the original state space representation. Throughout this section, we assume that the system is observable. If the system was not observable, then there would in general be no solution to the full state estimation problem.

The first step is to derive the similarity transformto transform the original state space representation of eqn. (3.79) to observable canonical form of eqn. (3.78). To achieve this, we begin by computing the observability matrixas defined in eqn. (3.73). Because the system is observable,is nonsingular; therefore,exists. Let the last column of be denoted as p so that

Using the fact that and focusing only on the last column yields

Definingwe havewhich shows that the output matrix transforms correctly. Next, consider the rows of

Using the fact that

we have that for

Definingwe are ready to consider the product

which has the desired form for the observable canonical form. Therefore, the similarity transform defined by U transforms the original observable system to observable canonical form.

In the observable canonical form, it is straightforward to design the observer gainbecause

which has the characteristic equation

Therefore, if a set of desired discrete-time pole locationsare selected, then the desired characteristic equation can be computed. The vectorto cause eqn. (3.80) to match the desired characteristic equation can be computed and

Example 3.16 Consider the system described in eqn. (3.4) with m =1, b = 2 and k = 0. Defining the state vector ascontinuous-time state space model for the system is

For a sample period of T = 0.1 seconds, the equivalent discrete-time state space model given by eqn. (3.65) is

The observability matrix is

so that

The resulting similarity transform uses

With the closed loop estimator poles (i.e. the eigenvalues ofand ofspecified to be atThe observer gain matrices are

 

 

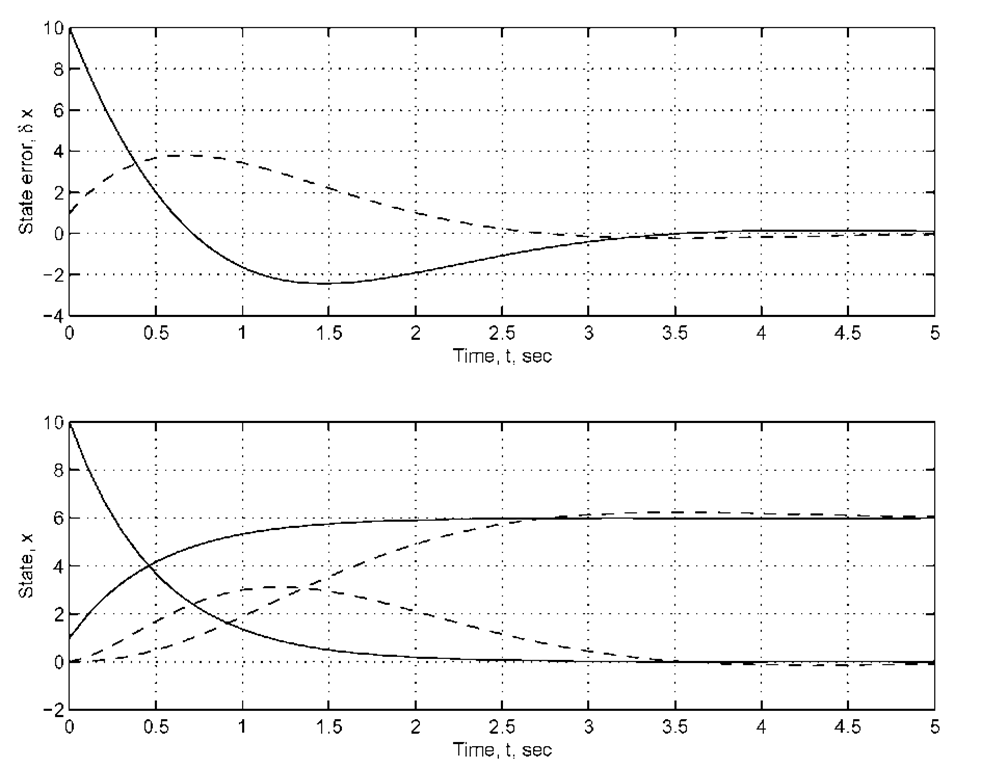
Figure 3.6: State estimator simulation for Example 3.16. Top – State estimation error versus time. The solid line isand the dashed line is Bottom – State and state estimates versus time. The solid lines are the states and the dashed lines are the estimates.

The convergence of the resulting state estimator is shown in Figure 3.6 for the initial conditionsThe top plot shows the estimation error with xi as a solid line and X2 as a dashed line. The bottom plot shows state (solid) and the estimated state (dashed). Both plots clearly show the convergence of the estimation error to zero. The plots are shown as continuous lines, but the state estimates are actually only defined at the sampling instants. A

There are clearly a variety of tradeoffs in the selection of the state estimation gain vector. If L is small then the convergence will be slow, but measurement noise will have a small effect on the state estimates. Alternatively, when L is large convergence of the error will be rapid, but measurement noise will have a relatively large effect on the state estimates. When it is possible to propagate estimates of the accuracy of the state estimates and of the measurement accuracy, then it is interesting to consider the time-varying gain vector that provides an optimal tradeoff between the accuracy of the state and measurements.