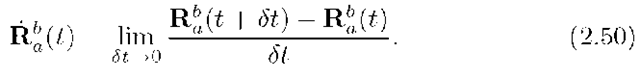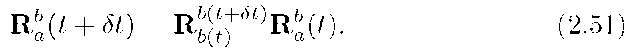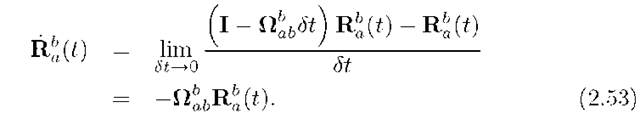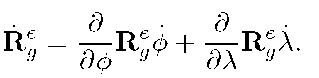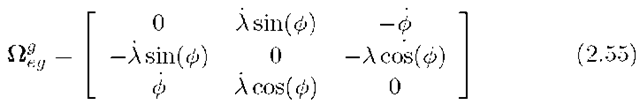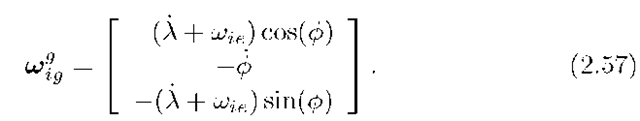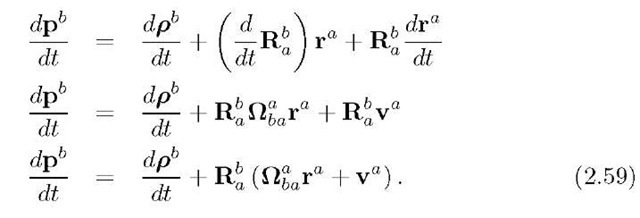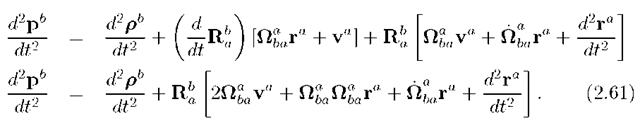As discussed relative to Figure 2.1, reference frames may be free to rotate arbitrarily with respect to one another. Consider for example the body frame moving with respect to the ECEF frame. The following subsections are concerned with frames-of-reference rotating with respect to one another.
Direction Cosine Kinematics
Section 2.5 showed that the transformation of vectors between two coordinate systems could be represented by an appropriately defined direction cosine matrix. In subsequent sections, it is necessary to calculate derivatives of direction cosine matrices for coordinate systems experiencing relative rotation. Such derivatives are the subject of this present section.
The definition of the derivative of the rotation matrix from frame a to frame b is
For small
the rotation
can be considered as the rotation from frame a to frame b at time t followed by the rotation from frame b at time t to frame b at time
Because the instantaneous angular velocity
of frame b with respect frame a represented in frame b is finite and St will be approaching zero, the rotation matrix
represents the small angle rotation
which by eqn. (2.48) is
where
Substituting eqns. (2.51) and (2.52) into eqn. (2.50) yields
Using the facts that
can also be expressed as
Example 2.6 Let a represent the geographic frame and b represent the ECEF frame. Using the fact the
we can compute
as the vector form of 
For 
as defined in Section 2.5.3, we can compute 
as defined in Section 2.5.3, we can compute
After algebra to simplify the result, this product yields
which gives
This, combined with
gives
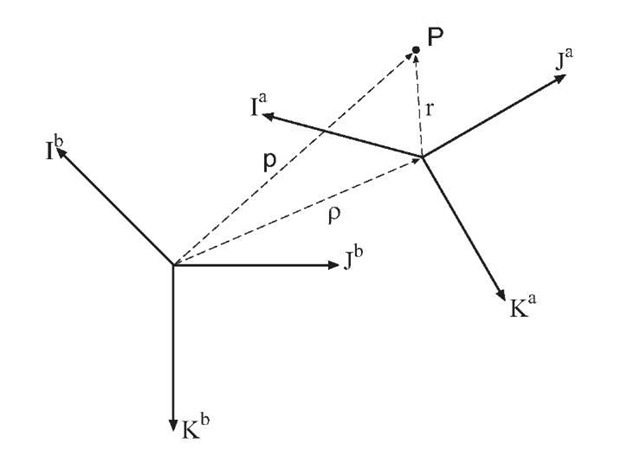
Figure 2.17: Rotating coordinate frames.
Derivative Calculations in Rotation Frames
As shown in Figure 2.17, let p be the vector from the b frame origin to point P, p be the vector from the b frame origin to the a frame origin, and r be the vector from the a frame origin to point P. These vectors are related by 
If
are known, then from Section 2.4, the representation of p in frame b can be computed:
If the a frame is rotating with respect to the b frame, the rate of change of
can be expressed as in eqn. (2.59):
The first term on the right accounts for the relative instantaneous linear velocity of the two reference frames. The second term is the instantaneous velocity of point P relative to the b frame due to the relative rotation of the a frame. The last term is the transformation to the b frame of the instantaneous velocity of point P relative to the origin of the a frame.
This equation can be considered as a special case of the following theorem, which is a statement of the Law of Coriolis.
Theorem 2.1 If two frames-of-reference experience relative angular rotation
with
then the time rate of change of the vector in the two coordinate systems are related by 
Taking a second derivative of eqn. (2.59) gives
Note the following points regarding the derivation of eqn. (2.61): the equation is exact; the equation is applicable between any two coordinate systems; and, the equation is linear in the position and velocity vectors. This equation is the foundation on which a variety of navigation systems are built.
