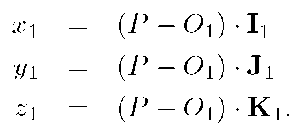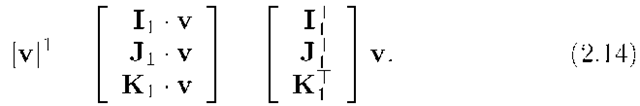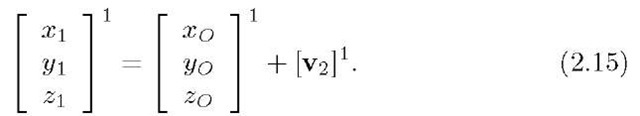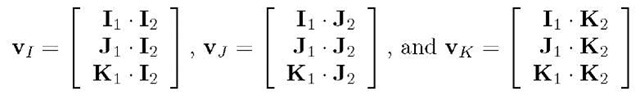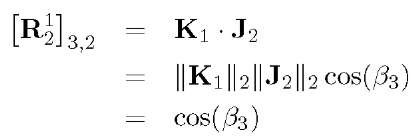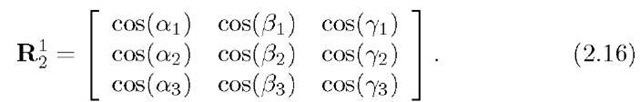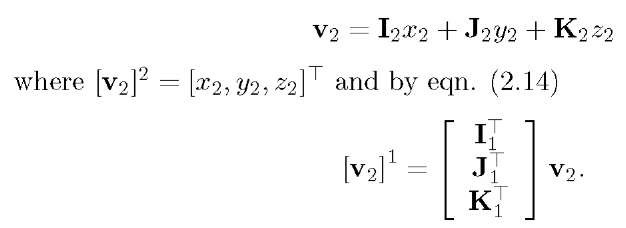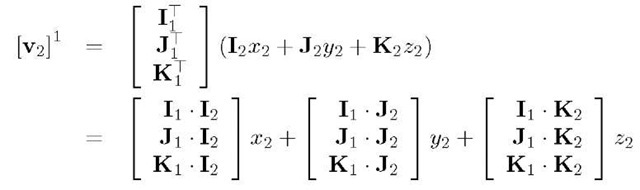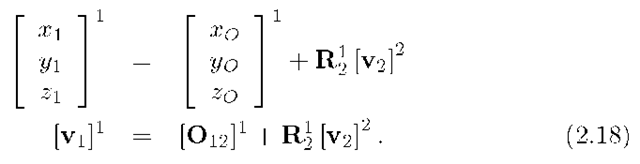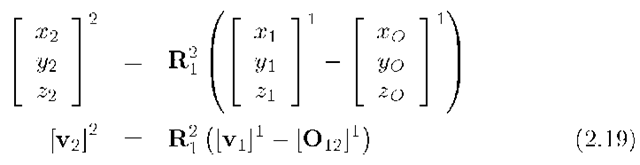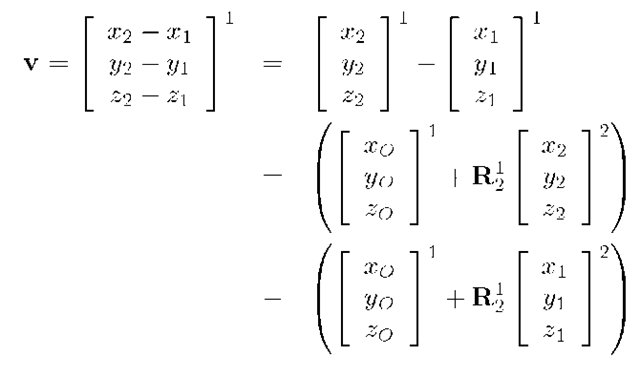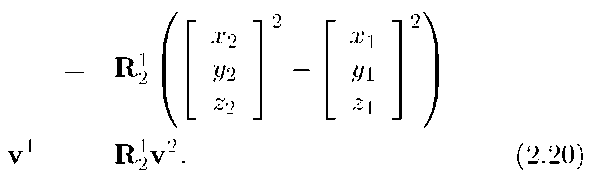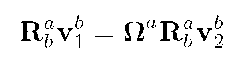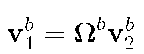This section presents methods for transforming points and vectors between rectangular coordinate systems. The axes of each coordinate system are assumed to be right-handed and orthogonal. Three dimensions are used throughout the discussion; however, the discussion is equally valid for
The Direction Cosine Matrix
Let
represent a right-handed orthogonal coordinate system. Let
be a vector from the origin
of the
frame to the point P. The representation of the vector
with respect to frame
is
axes and where
are unit vectors along the 
axes and
The vector
contains the coordinates of the point P with respect to the axes of
and is the representation of the vector
with respect to
The physical interpretations of the coordinates is that they are the projections of the vector
onto the
axes. For the two-dimensional x — y plane, the discussion of this paragraph is depicted in Figure 2.9.
A vector v can be defined without reference to a specific reference frame. When convenient, as discussed above, the representation of
with respect to the axes of frame
is
Eqn. (2.14) is used in derivations later in this subsection.
Figure 2.9: Two dimensional representation of the determination of the coordinates of a point P relative to the origin
of reference frame.
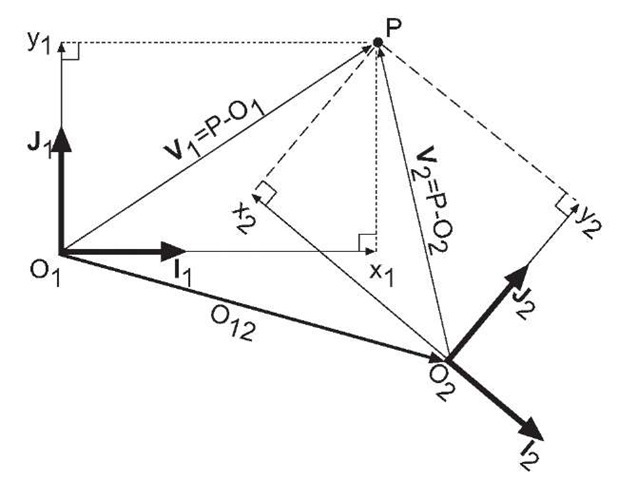
With two distinct reference frames
the same point can be represented by a different sets of coordinates in each reference frame.The remainder of this section discusses the important question of how to use the coordinates of a point in one frame-of-reference to compute the coordinates of the same point with respect to a different frame-of-reference. The transformation of point coordinates from one frame-of-reference to another will require two operations: translation and rotation.
From the above discussion,
is the vector from
to P and
is the vector from
Define
as the vector from
Therefore, we have that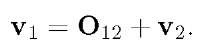 
This equation must hold whether the vectors are represented in the coordinates of the
frame or the
frame.
Denote the components of vector
relative to the
frame as
the components of
relative to the
frame as
and the components of
relative to the
frame as
Assume that
and the relative orientation of the two reference frames are known. Then, the position of P with respect to the
frame can be computed as
Because it is the only unknown term in the right hand side, the present question of interest is how to calculate
based on the available information.
Figure 2.10: Definition of the coordinates of a point P with respect to two frames-of-reference
Let
represent the unit vectors along the axes. As discussed relative to eqn. (2.14), vectors
defined as
represent the unit vectors in the direction of the
coordinate axes that are resolved in the
reference frame. Since
are orthonormal, so are
Therefore, the matrix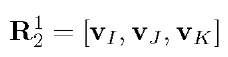 
is an orthonormal matrix
Each element of
is the cosine of the angle between one of
and one of
To see this, consider the element in the third row second column:
where
is the angle between
and we have used the fact that 
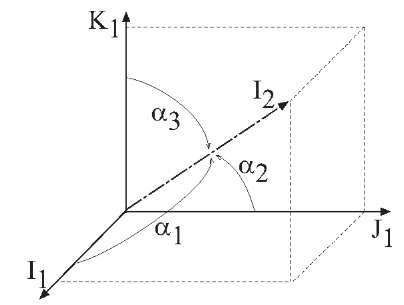
Figure 2.11: Definition of
in eqn. (2.16).
Because each element of
is the cosine of the angle between one of the coordinate axes of
and one of the coordinate axes of
the matrix 
is referred to as a direction cosine matrix:
Figure 2.11 depicts the angles .
for
that define the first column of
The
angles are defined similarly. When the relative orientation of two reference frames is known, the direction cosine matrix 
is unique and known.
Although the direction cosine matrix has nine elements, due to the three orthogonality constraints and the three normality constraints, there are only three degrees of freedom.
Therefore,
Point Transformation
When eqn. (2.17) is substituted into eqn. (2.15) it yields the desired equation for the transformation of the coordinates of P with respect to frame 2, as represented by
to the coordinates of P with respect to frame 1, as represented by
The reverse transformation is easily shown from eqn. (2.18) to be
where we have used the fact that
where the last equality is true due to the orthonormality of RJ. Note that the point transformation between reference systems involves two operations: translation to account for separation of the origins, and rotation to account for non-alignment of the axis.
Vector Transformation
Consider two points
Let the vector v denote the directed line segment from
Relative to
v can be described as
Eqn. (2.20) is the vector transformation between coordinate systems. This relation is valid for any vector quantity. As discussed in detail in [95], it is important to realized that vectors, vector operations, and relations between vectors are invariant relative to any two particular coordinate representations as long as the coordinate systems are related through eqn. (2.20). This is important, as it corresponds to the intuitive notion that the physical properties of a system are invariant no matter how we orient the coordinate system in which our analysis is performed.
In the discussion of this section, the two frames have been considered to have no relative motion. Issues related to relative motion will be critically important in navigation systems and are discussed in subsequent sections.
Throughout the text, the notation
will denote the rotation matrix transforming vectors from frame a to frame b. Therefore,
Matrix Transformation
In some instances, a matrix will be defined with respect to a specific frame of reference. Eqns. (2.21-2.22) can be used to derive the transformation of such matrices between frames-of-reference.
Let
be a matrix defined with respect to frame a and
be two vectors defined in frame a. Let b be a second frame of reference. If
are related by 
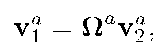then eqns. (2.21-2.22) show that
or
where
is the representation of the matrix
with respect to frame b.
