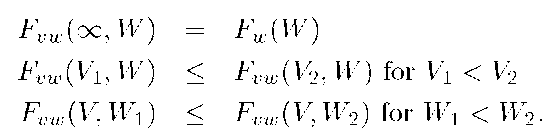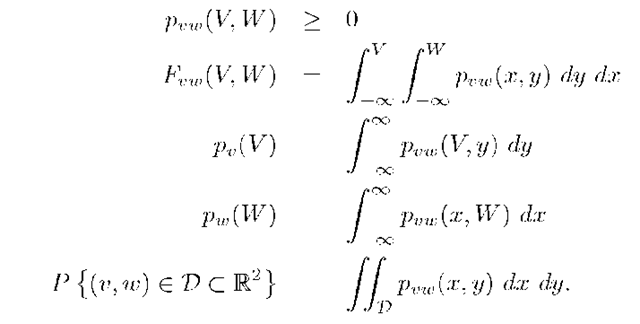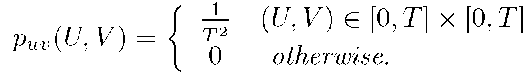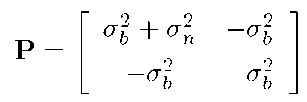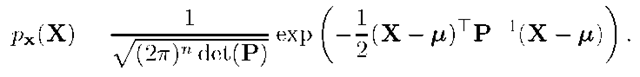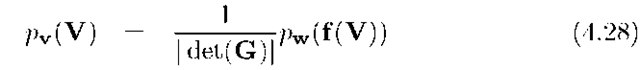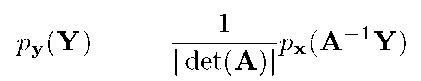Multiple Random Variables (GPS)

Navigation systems frequently involve multiple random variables. For example, a vector of simultaneous measurements y might be modeled as

where y represents the signal portion of the measurement and v represents a vector of random measurement errors.

In the case of multiple random variables, we are often concerned with how the values of the elements of the random vector relate to each other. When the values are related, then one of the random variables may be useful for estimating the value of the other. Important questions include: how to quantify the interrelation between random variables, how to optimally estimate the value of one random variable when the value of the other is known, and how to quantify the accuracy of the estimate. In this type of analysis, the multivariate density and distribution and the second order statistics referred to as correlation and covariance are important. The discussion of basic properties will focus on two random variables, but the concepts extend directly to higher dimensional vectors.

Basic Properties

Let v and w be random variables. The joint probability distribution function of v and w is

The joint distribution has the following properties:

 

 

The last two properties state the the joint distribution is nondecreasing in both arguments.

The joint probability density is defined as

The joint density has the following properties:

In the above,are referred to as the marginal density of v andrespectively. When the meaning is clear from the context, the subscripts may be dropped on either the distribution or the density.

Example 4.6 Let u and v be random variables with the joint probability density

Using the properties above, it is straightforward to show that

Statistics and Statistical Properties

Two random vector variables v and w are independent if

When two random variables are independent and have the same marginal densities, they are independent and identically distributed (i.i.d.).

Example 4.7 The random variables u and v in Example 4-6 are independent.

There is a result called the central limit theorem [31, 107] that states that if

where theare independent random variables, then as N increases the distribution forapproaches a Gaussian distribution, independent of the distributions for the individualThis rather remarkable result motivates the the importance of Gaussian random variables in applications. Whenever a random effect is the superposition of many small random affects, the superimposed effect can be accurately modeled as a Gaussian random variable.

When two random variables are not independent, it is useful to have metrics to quantify the amount of interdependence. Two important metrics are correlation and covariance.

The correlation -matrix between two random variables v and w is defined by

The covariance matrix for two vector valued random variables v and w is defined by

The correlation coefficientis a normalized measure of the correlation between the two scalar random variables v andthat is defined as

The correlation coefficient always satisfiesWhen the magnitude of pvw is near one, then knowledge of one of the random variables will allow accurate prediction of the other. Whenthen v and w are said to be uncorrelated. Uncorrelated random variables have andIndependent random variables are uncorrelated,but uncorrelated random variables may or may not be independent. Two vector random variables v and w are uncorrelated ifTwo vector random variables v and w are orthogonal if

Example 4.8 Consider the random variables

whereis a uniform random variable. It is left to the reader to show that

These facts show that u and v are orthogonal and uncorrelated. However, it is also straightforward to show thatThe fact that the variables are algebraically related shows that u and v are not independent. A

Let the matrixbe the covariance matrix for the vector x.

Then by eqn. (4.23), the element in the i-th row and j-th column of P is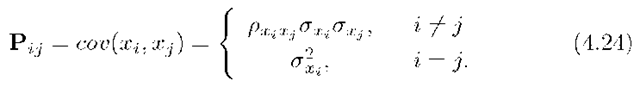

Therefore, knowledge of the covariance matrix for a random vector allows computation of the variance of each component of the vector and of the correlation coefficients between elements of the vector. This fact is very useful in state estimation applications.

Example 4.9 An analyst is able to acquire a measurement y that is modeled as

The measurement is a function of two unknowns a and b and is corrupted by additive measurement noiseThe analyst has no knowledge of the value of a, but based on prior experience the analyst considers a reasonable model for b to beThe random variables b and n are assumed to be independent. Bothare positive.

Based on this model and prior experience, the analyst chooses to estimate the values of a and b as

The parameter estimation errors areWhat are the mean parameter estimation errors, the variance of the parameter estimation errors, and the covariance between the parameter estimation errors?

Based on the results of Steps 3—5 and eqn. (4.23), the correlation coefficient between

If we define

then based on the above analysis

which checks with eqn. (4.24).

Analysis similar to that of Example 4.9 will have utility in Part II for the initialization of navigation systems. Related to this example, the case where a is a vector and the case where y is a nonlinear function of a are considered in Exercise 4.11.

Vector Gaussian Random Variables

For the vector random variablethe notationis used to indicate that x has the multivariate Gaussian or Normal density function described by

Again, the density of the vector Normal random variable is completely described by its expected valueand its covariance matrix

Transformations of Vector Random Variables

If v and w are vector random variables inrelated bywhere g is invertible and differentiable with unique inversethen the formula of eqn. (4.16) extends to

is the Jacobian matrix of g evaluated at W =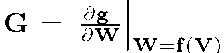

where

Example 4.10 Find the density of the random variable y where y = Ax, and A is a nonsingular matrix. Examples such as this are important in state estimation and navigation applications. By eqn. (4.28),

which is equivalent to

This shows that

This result is considered further in Exercise 4.10.

As demonstrated in Examples 4.4 and 4.10, affine operations on Gaussian random variables yield Gaussian random variables. Nonlinear functions of Gaussian random variables do not yield Gaussian random variables.