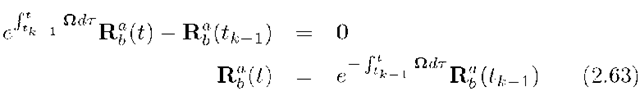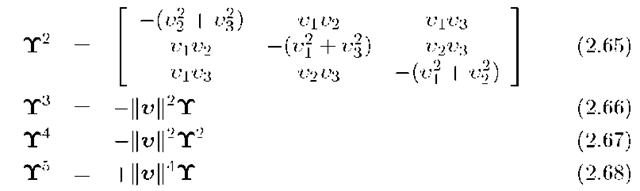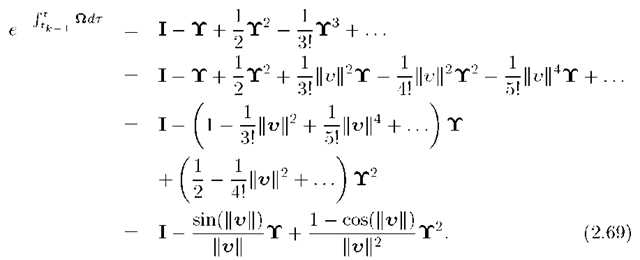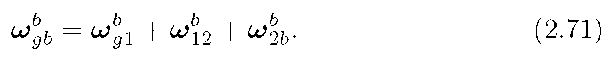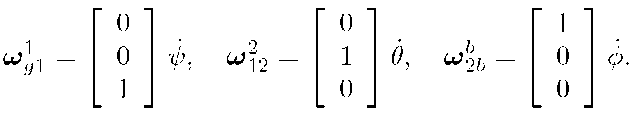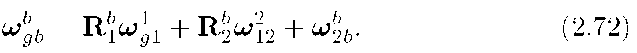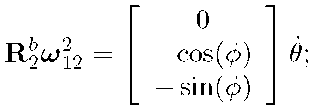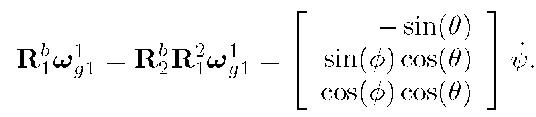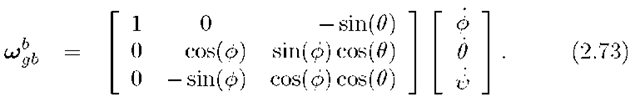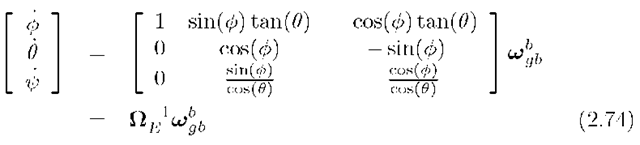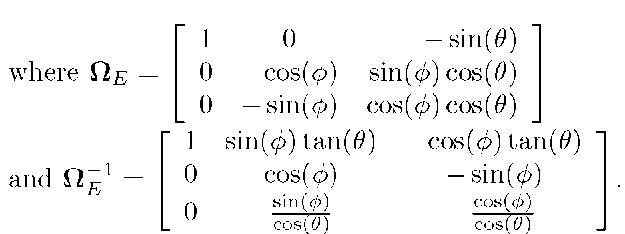Calculation of the Direction Cosine (GPS)

The previous sections have motivated the necessity of maintaining accurate direction cosine matrices. The following two subsections will consider two methods for maintaining the direction cosine matrix as the two reference frames experience arbitrary relative angular motion. Each technique relies on measuring the relative angular rate and integrating it (via different methods). Initial conditions for the resulting differential equations are discussed in Sections 10.3 and 11.7. Prior to integration, the angular rates should be properly compensated for biases and navigation frame rotation as discussed in Section 11.3.

The measurement of angular rates followed by integration to determine angle has the disadvantage that measurement errors will accumulate during the integration process. However, the approach has several distinct advantages. The angular rates are measurable via inertial measurements. Inertial measurements do not rely on the reception of any signal exterior to the sensor itself. Therefore, the accuracy of the measurement and integration processes will only be limited by the accuracy inherent to the instrument and of the integration process. Both of these quantities can be accurately calibrated so that the system accuracy can be reliably predicted. Also, the error accumulation through the integration of inertial quantities is a slow process that can be corrected via aiding sensors. Alternatively, level sensors and compass type instruments could be used to directly measure the Euler angles. However, level (gravity vector) sensors are sensitive to acceleration as well as attitude changes; and, yaw/heading sensors are sensitive to local magnetic fields. The resulting measurement errors are difficult to quantify accurately and reliably at the design stage.

Direction Cosine Derivatives

Eqn. (2.53) provides a differential equation which can be integrated to maintain the direction cosine matrix. Such an approach could numerically integrate each of the direction cosine elements separately; however, since the equation is linear, a closed form solution should be obtainable. Direct numeric integration of eqn. (2.53) does not enforce the orthogonality nor normality constraints on the direction cosine matrix; hence, additional normalization calculations would be required.

Letand select T sufficiently small thatcan be considered constantTo derive a closed form solution to eqn. (2.53) with initial conditiondefine the integrating factor

wherehas been used as a shorthand notation forto decrease the complexity of the notation. Thenotation is defined in eqn. (B.15).

Multiplying the integrating factor into eqn. (2.53) and simplifying, yields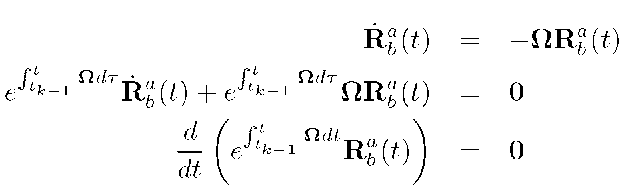

where the last step is valid given the assumption that T is sufficiently small so thatis constant over the period of integration. Integrating both sides, over the period of integration yields

To simplify this expression, let

wherePowers of the matrixreduce as follows:

which are verified in Exercise 2.10. Therefore, using eqn. (B.42),

Substituting eqn. (2.69) into eqn. (2.63) yields

whereEqn. (2.70) is properly defined theoretically, even asbut must be implemented numerically with care.

The designer must ensure that the intervalis sufficiently small (i.e., the sample frequency is sufficiently fast) to satisfy the assumption above eqn. (2.62) that eachcan be considered constant over each period of integration.

Euler Angle Derivatives

Section 2.5 defined the Euler anglesand described their use to determine the direction cosine matrixThis method of determining the direction cosine matrix requires the navigation system to measure or compute the Euler angles. This section presents the method for computing the Euler angle derivativesfrom the angular rate vector The navigation system could then integrate the Euler angle derivatives, to determine the Euler angles from which the direction cosine matrix can be computed.

Note that the three-tupleis not related toby a rotational transform because each of the components ofis defined in a different reference frame. Instead, we have that

Figures 2.14-2.16 define the yaw, pitch, and roll rotations. In addition, the figures show thatis the rate of rotation about the K oraxes, which are coincident; that _ is the rate of rotation about theaxes, which

are coincident; and, thatis the rate of rotation about theaxes, which are coincident. From the facts in the previous sentence we have that

From eqn. (2.71) we have

From eqn. (2.42),

and from eqns. (2.41-2.42),

Therefore, eqn. (2.72) yields

The inverse transformation is

Neithernor its inverse is a rotation matrix. Eqns. (2.73) and (2.74) do not represent vector transformations between frames-of-reference. The matrixis singular when

Eqn. (2.74) is a nonlinear ordinary differential equation for the Euler angles. Numeric integration of eqn. (2.74) provides estimates of the Euler angles from which the direction cosine matrix can by computed using eqn. (2.43). This approach requires numerous trigonometric operations at the high rate of the attitude portion of the INS system.