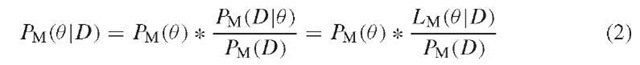1. Introduction
The genetic patterns observed today in the human species are the result of a complex history including population expansions and collapses, migration, colonization, extinction, and admixture events. These events have taken place in different locations and times, sometimes involving populations that have been separated for centuries or millennia. Given that anatomically modern humans probably appeared some 100-200 thousand years ago (KYA) in Africa, it would certainly be ingenuous to think that the details of that history will be fully uncovered using genetic data. However, it would probably be equally misguided to refuse the use of simple models on those grounds.
Indeed, genetic data have revolutionized the way we look at our species in many ways. They have shown that the split between human, chimpanzees, and gorillas is rather recent, between 5 and 8 million years old (Nichols, 2001), instead of twice as much as was originally believed on the basis of morphological and fossil data. They have shown that the amount of genetic variation within single populations represents a major proportion (~85-90%) of the diversity present in the human species as a whole, indicating that despite the sometimes large phenotypic differences between some human groups, genetic diversity is not very strongly partitioned. They have contributed to the debate over recent migration patterns, the emergence of our species, or its relationships with Neanderthals. In particular, genetic data have been the major driving force in favor of a recent origin of our species, notably thanks to work done using mitochondrial DNA data in the late 1980s and early 1990s (Cann et al., 1987; see also Article 5, Studies of human genetic history using mtDNA variation, Volume 1).
The modeling work performed in this period showed a significant genetic signal for a demographic bottleneck followed by a demographic expansion, the dating of which was recent (i.e., less than 200 KYA, Slatkin and Hudson, 1991; Rogers and Harpending, 1992), a result found across genetic markers, including independent microsatellite loci (Goldstein et al., 1995; Reich and Goldstein, 1998). These inferences appeared to reject the so-called multiregional (MR) model and to favor a model of recent expansion out of Africa (RAO for recent African origin or OOA for out of Africa), which had the advantage that it correlated with the first appearance of anatomically modern humans. The MR model, which should probably be seen as a family of models (Goldstein and Chikhi, 2002), assumes an ancient origin (more than 1 million years ago, MYA) of human populations. It also posits some regional continuity between present-day populations in the different continents and the early migrations out of Africa of archaic hominids. The RAO model also had the advantage of explaining the limited diversity observed in humans and the lack of strong differentiation between present-day populations, both being higher in chimpanzees despite their much more limited geographical range and census sizes. Thus, in the mid-1990s, the picture could not have been clearer and it seemed to many that only the details needed to be worked out. Fifteen years later, one has to admit that it could not be further from the truth. The increasing use of independent genetic markers, including coding genes, and the rather different modeling assumptions used by various authors have led to a confusing literature from which opposite conclusions have been drawn (Excoffier, 2002). Even assuming that there is a general genetic signature for a recent demographic expansion, it is not necessarily straightforward to conclude in favor of the RAO, as noted by Wall and Przeworsky (2000) and others. The link between genetic results and archaeological, linguistic, or anthropological debates and controversies is not as simple as some would like to believe.
The aim of this article is to describe some of the simple models that have been used to decipher broad trends in that complex history. Principles underlying demographic inference based on genetic data are presented. In particular, we show how summary statistics are differentially influenced by demographic events such as expansions and contractions. We also present some results from the coalescent theory, which focuses on the properties of gene trees and plays a major role in population genetics modeling. We then discuss some recent methodological developments including Bayesian and the so-called approximate Bayesian computational methods (Beaumont et al., 2002; Marjoram et al., 2003; Beaumont and Rannala, 2004) and try to address a number of the issues that are the focus of ongoing research, including the use of ancient DNA data or the use of patterns of linkage disequilibrium (LD) in the genome (Stumpf and Goldstein, 2003; see also Article 1, Population genomics: patterns of genetic variation within populations, Volume 1).
Given the ever-increasing importance attached to genetic data, by nongeneticists and geneticists alike, it should be stated at the outset that the amount of information that can be extracted from genetic data to infer past events is often limited and consequently requires a priori assumptions. There are two fundamental problems: (1) Genetic data only contain information on the relative rates of different processes in the history of the population. This means that it is impossible to make statements about the times of events or population sizes without some external reference, such as mutation rates, or the dating of splits of populations from archaeological evidence. (2) As discussed below, population genetics theory suggests that the vast majority of genes in humans that lived in the past have left no descendent copies today owing to genetic drift, and consequently there will be no simple relation between the history told by archaeological remains and that told by the genes.
2. Principles of demographic inference from genetic data: information extracted from summary statistics and gene tree shapes
In this section, we describe how the demographic history influences genetic patterns by first describing its effects on some summary statistics and then on the shape of gene trees. This allows us to review some results of the coalescent theory and then address some issues regarding parameter inference.
2.1. Summary statistics are differentially affected by demographic events
The detection and quantification of past demographic events relies on the fact that specific events leave a genetic signature in present-day populations. Meaningful inference will therefore be possible only if these signatures are sensitive to specific demographic scenarios, and unlikely to be affected by others. A richly explored area of analysis has been the study of the effect of changes in population size on different summary statistics. For instance, a stationary (or stable) population can be characterized by the scaled mutation rate 0 = 4Ne^ (for diploids) where Ne is the effective population size and \x the locus mutation rate. There are different estimators of 0, on the assumption of a stationary population, which are based on different summary statistics calculated from the data (see below). If the population is growing or contracting, the expected values of these estimators diverge from each other, and this can be used to detect population growth or decline.
A commonly used statistic that summarizes genetic diversity is the heterozygosity expected under Hardy-Weinberg conditions He = 1 — J](nt/n)2 where nt is the observed allelic count of the i th allele. Under an infinite allele model, Kimura and Crow (1964) showed that in a stable population E[He] = 0/(0 + 1), which can be used to obtain an estimate of 0. Another way to estimate 0 comes from the work of Ewens (1972) who studied the sampling properties of neutral alleles in a demographically stable population for the infinite allele model. Ewens showed that at mutation-drift equilibrium, the expected number of distinct alleles, nA, in a sample of size n is a function of n and 0 only:
Under these null-model conditions, he also characterized the expected allelic frequency distribution, showing that it is a function of 0, n, and nA. This distribution obtained from what is now known as Ewens’ sampling formula, provided the means for testing departures from the null-model (Watterson, 1978). Indeed, He values can be computed using nt values or using Ewens’ sampling formula (i.e., ignoring allelic counts). In fact, Watterson originally used the homozygosity that is equal to 1 – He, but He is more commonly used now. Significant differences between the two He values can then be interpreted in terms of departures from any of the neutrality, size constancy, or mutation model assumptions. When large populations go through a bottleneck, rare alleles are lost first, thereby reducing nA significantly. Since He computed as 1 — J](nt/n)2 is little influenced by rare alleles (their frequency is squared), high He values will be maintained for relatively longer periods. Thus, observed He values will be significantly higher than those expected conditional on nA and equilibrium conditions. Conversely, expanding populations will tend to accumulate new (and hence rare) alleles, and significantly lower values of He will be observed, so long as a new equilibrium is not reached. Simple summary statistics such as nA and He thus contain information on ancient demographic events. So long as simple demographic histories and a simple mutation model can be assumed, a straightforward interpretation is possible.
Since the early work of Ewens and Watterson, the approach has been extended to apply to different mutation models and hence to different genetic markers (Tajima, 1989a,b; Fu and Li, 1993) and different summaries of the data. For instance, Marth et al. (2004) studied the properties of the full allele frequency spectrum under different demographic scenarios, and found computationally quick ways to estimate these frequency spectrums. Similar approaches based on other aspects of the allelic distribution have been used. For microsatellites, whose alleles are defined by the size of an amplified DNA fragment consisting of small repeated units, Reich and Goldstein (1998) suggested to use an index of peakedness mathematically related to the distribution’s kurtosis. The rationale was that stable populations tended to have ragged allelic distributions, whereas expanding populations had smoother, often unimodal distributions. With a similar rationale, Garza and Williamson (2001) showed that bottlenecked populations tended to have gappy allelic frequency distributions, whereas the allelic range was little affected.
For DNA sequence data, He and nA are not the most appropriate measures of diversity because they do not account for the amount of mutations between alleles. The mean number of nucleotide differences between sequences, n, and S, the number of segregating sites (i.e., single-nucleotide polymorphisms or SNPs) are more suitable. Both statistics have been shown to provide two estimators, 0S and 0n, of the scaled mutation parameter, 0, at mutation-drift equilibrium and to be differentially affected by demographic events and selection (Tajima, 1989a,b). Tajima (1989a) hence suggested the use of D = (0n — 0S)/[Var(0n — 0S)]1/2, as a measure of departure from equilibrium conditions. Demographic bottlenecks and balancing selection tend to reduce S without affecting n very much and hence to produce positive D values, whereas population expansions and positive selection (selective sweeps) tend to produce negative values. As we shall see below, the situation is actually more complicated (see Article 4, Studies of human genetic history using the Y chromosome, Volume 1 and Article 5, Studies of human genetic history using mtDNA variation, Volume 1).
2.2. The shape of gene trees
Where an ordinal genetic distance can be defined between alleles, such as DNA sequences, and microsatellite alleles, it is possible to summarize or represent genetic diversity, not by a number, like n or He, but by a distribution of allelic pairwise distances. These pairwise difference or mismatch distributions have been extensively used and are also sensitive to demographic events (Slatkin and Hudson, 1991; Rogers and Harpending, 1992). Since, the interpretation of such distributions is easier from a gene tree perspective, we first review some results of the coalescent theory, which is the backbone of population genetic modeling. The coalescent theory provides important results on the probability distribution of genealogies (and hence on their shape) arising as a limiting case under a class of population genetics models such as the Wright-Fisher and Moran models. One major result of the standard coalescent is that in a sample of size n, the time Tn during which there are n lineages (i.e., until the first two lineages coalesce) follows an exponential distribution of parameter = n(n — 1)/4Ne, where Ne is the effective population size. Its expectation is E[T„] = 1/A.„ = 4Ne/n(n — 1).
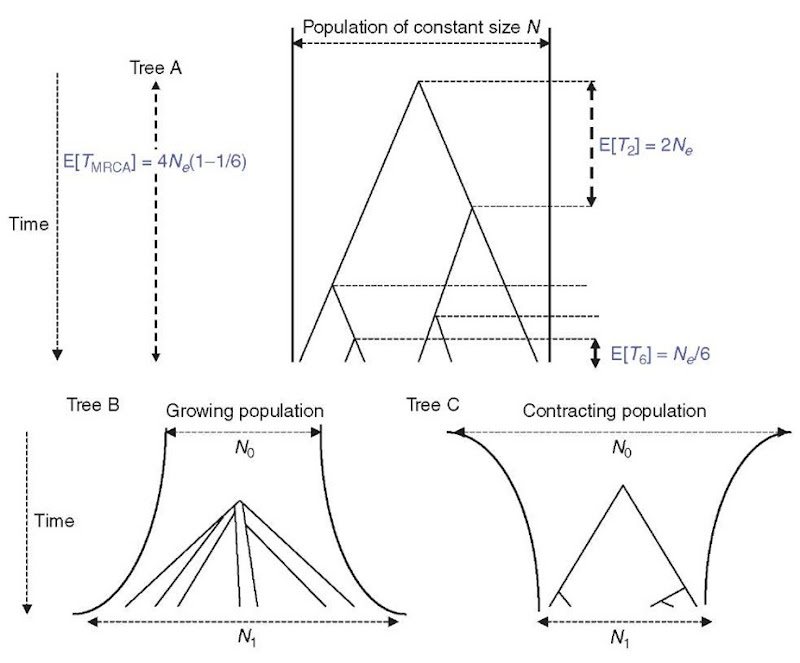
Importantly, coalescent times are functions of Ne and n, and are independent of the mutational process, so long as neutrality can be assumed. After the first coalescent event, the number of lineages decreases to n — 1 and the following coalescent time is sampled from the new exponential distribution with parameter Xn—j and expectation E[Tn—j] = 4Ne/(n — 1)(n — 2). This process continues until the most recent common ancestor (MRCA) of the sample is reached. The time to the MRCA represents the height of the gene tree and has an expectation of E[Tmrca] = E[T„] + E[T„—1] + … + E[T2] = 4Ne(1 — 1/n). Thus, for reasonably large sample sizes, E[TMRCA] ~ 4Ne at equilibrium, and the TMRCA of the sample is nearly equal to the TMRCA of the population. The structure of this null-model tree is interesting as most of the coalescent events take place near the branches tips. For n = 50, coalescence times will vary, in expectation, by more than 3 orders of magnitude, with the first 25 and 35 coalescent events taking place in the first 2 and 5% of the tree’s height, respectively. In contrast, the last coalescent event has an expectation of 2Ne, that is, half the tree’s height. The tree is thus typically dominated by the last two branches in an equilibrium population.
For populations with monotonic size changes, it is straightforward to infer expected tree shapes (Figure 1). An expanding population can be seen as having its Ne decreasing backward in time. Thus, expected coalescence times will also decrease with Ne. Hence, compared to a stable population of similar size today, coalescent events will concentrate around the MRCA, producing a “starlike” tree. By contrast, in a declining population, coalescence times are moved toward the present and the tree has a “comblike” shape. Assuming a high enough mutation rate, a starlike tree is expected to produce alleles that have evolved more or less independently since the MRCA and mutations will accumulate along branches of similar lengths. Hence, going back to mismatch distributions, we expect them to be unimodal and roughly Poisson-like (Slatkin and Hudson, 1991). By contrast, stable populations are expected to produce ragged mismatch distributions with at least two modes (since the tree is dominated by the last branches).
Figure 1 Coalescent trees. Tree A is the tree expected under a simple Wright-Fisher model (population size constant, no selection). Tree B is expected under a population growth. Tree C is expected under a model of population contraction
It may be worth noting that we presented the properties of the true gene trees, which are usually unknown. In practice, trees have to be estimated using polymorphism data, which are dependent on the mutation process and the time since the MRCA. When the total number of mutations is low, we may not be able to separate a starlike from a comblike tree. Similarly, when the number of mutations is high in a starlike phylogeny and if homoplasy is important, as in microsatellite loci, similar alleles may be generated by long branches that will reduce the expansion signal by creating false short branches.
Despite being a limiting case, the coalescent is extremely popular among population geneticists because it is fairly robust to details of life history (Donnelly and Tavare, 1995), and coalescent simulations are also extremely fast (samples, rather than populations are simulated). The standard coalescent has also been extended to account for population structure, recombination within the locus of interest, and different forms of selection, a thorough review of which is given by Nordborg (2001).
In the next section, we discuss some of the ongoing research on population genetic modeling and some of problems that still need to be addressed in coalescent-based modeling.
3. Improving the use of genetic information: increasingly complex models for increasingly complex data
3.1. Bayesian and approximate Bayesian methods: the use of rejection, importance sampling, and Markov chain Monte Carlo algorithms
Following Felsenstein’s (1992) remark that summary statistics discard most of the information present in genetic data, recent genetic modeling has seen the development of a number of statistical approaches that try to extract as much information as possible from the full allelic distributions.
Likelihood-based approaches aim at computing the probability PM(D\0) of generating the observed data D under some demographical model M, defined by a set of parameters 0 = (0\,… ,0k). This probability, which can be seen as a function of 0 (since M is assumed and D is given) is the likelihood LM(0 \D), or simply L(0). Some methods try to find the 0i values that maximize L(0), and use these maximum likelihood estimates (MLE) for the parameters of interest. Other likelihood-based approaches take a Bayesian perspective and try to estimate probability density functions for these parameters (rather than point estimates). Using Bayes formula, this can be written as:
Since the denominator PM(D) is constant, given the data, PM(0\D) is proportional to PM(0) ^ Lm(0\D). In the Bayesian framework, Pm(0) summarizes knowledge (or lack thereof) regarding the 0i before the data are observed and is referred to as the prior. PM(0 \D) is the posterior and represents new knowledge about the 0 i after the data have been observed. The posterior is thus obtained by weighting the prior with the likelihood function. While the use of priors involves some subjectivity, it has the advantage of making clear and explicit assumptions about parameters, rather than assuming point values for, say, mutation rates or generation times, as has often been the case in the past, for instance, to date population split events (Goldstein et al., 1995; Chikhi et al., 1998; Zhivotovsky, 2001).
The two previous approaches require the likelihood to be computed. It is theoretically possible to use coalescent simulations to generate samples under complex demographic models, and hence estimate PM(D\0) for many parameter values using classical Monte Carlo (MC) integration. In practice, however, these probabilities are so small that they cannot be estimated in reasonable amounts of time for most sample sizes (Beaumont, 1999). Efficiency can be improved by using importance sampling (IS), which aims to sample gene trees as closely as possible from their conditional distribution, given the data, thereby avoiding most of the genealogies that would be sampled in classical MC simulations (Griffiths and Tavare, 1994; Stephens and Donnelly, 2000). Another computer-intensive approach that has had some success in making inferences about demographic history is Markov chain Monte Carlo (MCMC), in which a Markov chain is simulated whose stationary distribution is the required Bayesian posterior distribution. Example applications to human population data include estimation of the amount and direction of gene flow in equilibrium models of migration-drift balance (Beerli and Felsenstein, 2001), the relative contributions of source populations in an admixture model (Chikhi et al., 2001), and the inference of ancestral size and splitting of human and chimpanzee populations (Rannala and Yang, 2003). A particularly exciting application of MCMC is in a model of migration with population splitting (Nielsen and Wakeley, 2001; Hey and Nielsen, 2004), which has recently been used to infer aspects of the recent demographic history of chimpanzees (Won and Hey, 2005), and undoubtedly will have useful applications in humans.
Most likelihood-based methods have not yet had the impact one would have expected. This is due to the fact that for most interesting demographic models the likelihood cannot be computed or approximated. Also, the computations are extremely time-consuming and hence cannot be applied to the increasing size of modern data sets. An exception here is computer-intensive methods for detecting admixture and cryptic population structure from multilocus genotypic data (Daw-son and Belkhir, 2001; Pritchard et al., 2000; Falush et al., 2003), but these are based on relatively simple approximations that do not include genealogical structure. However, they do point to one possible avenue in population genetics, the approximation of complex genealogical models, the parameters of which can then be inferred considerably more easily. Examples in this vein are the development of PAC likelihood (for product of approximate conditionals) to simplify inference with recombining sequence data (Li and Stephens, 2003), in which the coalescent is approximated by a simpler genealogy with more tractable analytical properties; the use of composite likelihood methods (Wang, 2003; McVean et al., 2004), where the full likelihood is reduced to simpler components that are treated as independent and multiplied together.
An alternative to the likelihood-based methods that use all the data is the development of approximate likelihood methods that measure summary statistics from the data, and then use simulations to find parameter values that generate data sets with summary statistics that match those in the data most closely. Data are simulated according to a model or set of models for a wide range of parameter values, either using a regular grid (e.g., Weiss and von Haeseler, 1998) or sampling from prior distributions (e.g., Pritchard et al., 1999). Parameter values that produce simulated data sufficiently close to the observed data are used to estimate the likelihood (Weiss and von Haeseler, 1998 on mtDNA data) or construct posterior distributions (Pritchard et al., 1999, on linked Y chromosome microsatellite data). For instance, Weiss and von Haeseler (1998) used the number of segregating sites S and n to measure similarity between data simulated under a model of population size change (exponential increase or decrease versus stability) and observed data. They accepted the ith simulated data (and corresponding parameter values) using the indicator function:
where 8 is some arbitrary tolerance level or threshold (see below).
By varying the exponential rate, the time since the population size started to change and , they constructed a grid of likelihood values. They then computed the ratio to the highest value to define confidence intervals. Applying this approach to a Basque sample, they found virtually no support for a model of constant or decreasing population size. The best support was for a recent exponential increase from an originally small population, which is in agreement with the relative isolation of Basques from other European populations.
Pritchard et al. (1999) also analyzed models of exponential size change, but used three summary statistics, the number of different haplotypes, the mean (across loci) of the variance in repeat numbers, and the mean heterozygosity across loci. They used an indicator function I 5 such that for the i th simulation Is(i) = 1 if the three relative differences \PSIM — Pobs\/Pobs are less than the tolerance 5, where P stands for any of the three parameters, and I5(i) = 0 otherwise. They applied this method to data from different continents and found strong support for a model of population growth for the whole world population (despite genetic differentiation between continents), and for East and South Africa, America, Europe, East, and West Asia but not for West Africa or Oceania. They also found that there was a huge uncertainty on t0, the time at which populations started to increase, and on TMRCA values, confirming as well that t0 and TMRCA are generally very different. Mean TMRCA values around 40 KYA had confidence intervals ranging between ~10 and more than 100 KYA. Another important result for the interpretation of results obtained under different genetic models was that constraints on allelic sizes could lead to significant changes in TMRCA values (but not so much on t0). For instance, the higher end of the TMRCA confidence interval could move from ~120 to ~320 KYA when constraints were accounted for.
Bayesian versions of these summary-statistic methods (such as Pritchard et al., 1999) have recently been dubbed “approximate Bayesian computation (ABC)” (Beaumont et al., 2002; Marjoram et al., 2003), and made more efficient. For example, Beaumont et al. (2002) have suggested improvements by applying a rejection algorithm as above, weighting the accepted parameter values according to their distance to the observed data, and correcting for the relationship between the parameter value and summary statistics in the vicinity of those calculated from the observed data. Marjoram et al. (2003) have proposed an MCMC algorithm where the acceptance or rejection of an update depends on whether the data or summary statistics thereof that arise from the update are within some distance of those observed in the data.
ABC methods are extremely flexible since they can be applied to any demographic model under which data can be simulated. It is also easier to add nongenetic information into the priors, which could be particularly relevant for integrating archaeological data into genetic modeling. Limitations stem from the difficulty to decide which summary statistics should be used and how the value of the tolerance 5 influences inference. Little has been done on these issues, but Beaumont et al. (2002) found that the improved ABC algorithm was little affected by 5 values whereas the simple rejection approach was strongly influenced.
Summary statistics do not need to be used in a likelihood framework. An example here is the study by Pluzhnikov et al. (2002) in which the distribution of summary statistics for different parameter values is estimated by simulations, and then compared with summary statistics in the data. Using this approach on multilocus sequence data, they found that European and Chinese populations did not fit with a stable population or exponentially growing population model. Recent work by Akey et al. (2004) studied the behavior of four summary statistics, Tajima’s D and Fu and Li’s D* and F*, and Fay and Wu’s H, under the standard neutral model and four additional demographical scenarios (an exponential expansion, a bottleneck, a two-island model and an ancient population split). They computed a score function on the basis of the absolute difference in average summary statistics from simulations under specific demographic scenarios with those in the data, and then chose parameter values that minimized this score. This was carried out for 132 genes sequenced in African-American and European-American samples and they were able to (1) estimate parameter values under different scenarios, (2) select reasonable scenarios for the different data sets, and (3) detect loci potentially under selection (outliers). For instance, they found that the European-American data set was most consistent with a bottleneck occurring 40 KYA, whereas the African-American sample was most consistent with either an expansion or an old and strong bottleneck. An interesting result is that out of the 22 loci potentially under selection under a standard model, only 8 were found to be outliers in the other four scenarios, and were termed “demographically robust selection genes”. In other words, the demographical history of populations can potentially account for many outlier genes, which could be interpreted as being under some form of selection based on departures from the standard neutral model. This study also showed that most of the deviations from neutrality and all the “demographically robust selection genes” were not shared by the European- and African-Americans and was interpreted as reflecting potential local adaptations. A similar approach based on mismatch distributions and a set of demographic models was followed by Marth et al. (2003).
As indicated by the study of Akey et al. (2004), summary-statistic approaches can be useful for detecting selection on individual loci or genomic regions when a large number of markers are analyzed. A recently productive area of analysis in this regard has been based on estimators of the parameter FST. This parameter, which is used to measure genetic differentiation between populations, can be interpreted as the probability that two genes chosen at random within a subpopulation share a common ancestor within that subpopulation. It is expected that neutral loci should follow some unknown distribution, and that outlier loci, potentially under selection, can then be detected, as originally suggested by Cavalli-Sforza (1966). It is possible to construct a null distribution of FST under simple models, typically island models, and see where the real data lie (Beaumont and Nichols, 1996). Another solution is to use large numbers of loci sampled randomly in the genome to account for the unknown demographic history (but common to all loci) as suggested by Goldstein and Chikhi (2002). The latter approach has been used for 26 000 SNPs in African, European, and Asians samples by Akey et al. (2002) who detected a number of outliers. It has also been used with microsatellite data on European and African samples (Storz et al., 2004), which has, remarkably, yielded similar patterns to that found by Akey et al. (2004). Indeed, the outlier loci all have substantially reduced variability in non-African populations, suggesting adaptive selective sweeps following the putative OOA expansion. Of course, these inferences are dependent on the demographic model assumed, and it may be possible, for example, that during a wave of advance some loci may be carried all the way with total replacement while others may be lost and replaced by indigenous markers, in which case a complex demography could mimic selection (Eswaran et al. 2005).
3.2. Increasing the complexity of models and the size of the data analyzed
In recent years, there has been increasing recognition and awareness that most of the models used to infer ancient demography were too simple. In this regard, an original and interesting modeling framework was recently developed by the group of L. Excoffier (Currat et al., 2004; Ray et al., 2003), which allows explicit spatial modeling of genetic data in which ecological information can be incorporated. First, complex demographical scenarios can be simulated using digitalized geographical maps made of cells arranged in a two-dimensional grid with defined carrying capacities and friction values (expressing the difficulty in moving through them). Samples are chosen on the digitalized map and coalescent simulations can then be carried out to simulate the genetic data of the populations of interest. Theoretical expectations of a number of summary statistics can be obtained under widely different scenarios and compared to observed data. This framework was implemented in the SPLATCHE software (Currat et al., 2004) and it was used in its simplest form (i.e., assuming no environmental heterogeneity) to study the effect of geographical expansions and varying levels of gene flow on the form of mismatch distributions (Ray et al., 2003). Currat and Excoffier (2004) also simulated the most realistic model to date, of the demographic expansion of humans in Europe and their interaction with Neanderthals. In this model, a range expansion of modern humans starts in the Near East with local logistic growth and a higher carrying capacity for humans over Neanderthals (to model a better exploitation of the environment by humans). Conditional on the fact that no Neanderthal mitochondrial DNA data are observed in humans today, coalescent simulations are carried out for different levels of admixture. Thus, using a summary-statistic approach akin to ABC methods, Currat and Excoffier (2004) demonstrate that the maximum level of admixture between Neanderthals and humans was most probably much lower than 0.1% (for the female line). This value in orders of magnitude lower than the lowest bound found using coalescent simulations that did not incorporate population structure. Thus, this study shows just how incorporating spatial structure into modeling can provide extremely different conclusions on admixture estimates.
Similarly, one of the most disputed issues in human genetics has been the detection of ancient bottlenecks and patterns of population growth. Wall and Przeworsky (2000) tried to put some order in the rather confusing literature, and concluded that the signal for a population bottleneck followed by an expansion detected in the early 1990s was mostly limited to mtDNA and Y chromosome data, and hence probably the result of selection on these loci. A more recent review by Excoffier (2002) concluded that most of the data disagreeing with a population expansion were from coding regions and could, therefore, be explained by balancing selection, as was suggested for the first time by Harpending and Rogers (2000). Thus, the signal for population expansion would actually be real. However, the balancing selection hypothesis predicts that regions of low recombination should exhibit high levels of genetic diversity, whereas Payseur and Nachman (2002) found exactly the opposite, namely, a positive relationship between local recombination rate and variability. Recently, this issue had a new development when Hellman et al. (2003) found that this positive correlation could actually be caused by a correlation between recombination and mutation rates. Thus, it appears that the complexity of patterns of genetic variation in the genome can hinder our ability to uncover patterns of ancient population growth (see Article 1, Population genomics: patterns of genetic variation within populations, Volume 1).
Even assuming that one concentrates on neutral markers, the literature on population growth has been rather confusing. Table 1 is an attempt at summarizing some of the modeling assumptions made regarding past population size changes. The point we would like to make with this table is that it is very difficult to compare quantitatively and even qualitatively the results obtained by studies when the demographical model assumed (exponential vs. sudden growth, with or without previous bottleneck) the markers analyzed (maternally inherited mtDNA vs. nuclear coding genes vs. paternally inherited Y chromosome haplotypes) and the statistical approaches differ that much.
Another level of complexity arises when one studies the temporal behavior of the summary statistics used to detect population size changes. For instance, Tajima’s D, which is probably the most popular of all statistics used to detect population expansions and bottlenecks, may be transiently positive and negative depending on the severity of the population size change and the number of generations since the original demographic event. After a bottleneck, D values will first be positive, then become negative when the population grows again, before tending towards equilibrium (Tajima, 1989b; Fay and Wu, 1999). Moreover, D is affected in a complex manner by increasing complexity of the mutation model. Simulations have shown that mutation rate heterogeneity within a locus can lower S , which could either lead to apparent signals of population bottlenecks, in an otherwise stationary population, or hide real population expansion signals by pushing D values in the opposite direction (Bertorelle and Slatkin, 1995; Aris-Brosou and Excoffier, 1996). More recently, hidden population structure was also shown to generate spurious results. Indeed, Ptak and Przeworski (2002) have shown that the number of “ethnicities” in the samples analyzed was negatively correlated to D. This can be understood by noticing that more diverse samples tend to contain a higher proportion of rare alleles, when populations are differentiated. Given that different loci can have different Nes, the temporal behavior of D could lead to apparently contradictory results depending on whether mtDNA or nuclear microsatellites are analyzed, as was indeed found (Harpending and Rogers, 2000). A similarly complex temporal behavior was found by Reich and Goldstein (1998) for their peakedness statistic or by Kimmel et al. (1998) for their “imbalance index”, making interpretations of these summary statistics more difficult than one would like.
Studies such as that of Akey et al. (2004) or Currat and Excoffier (2004) point to the importance of modeling population structure. However, an issue that has received very little attention is the influence of population extinctions despite the fact that early human groups were probably small enough to be subject to local extinctions. As noted by Eller (2002) and others (Sherry et al., 1998; Goldstein and Chikhi, 2002), the conservation genetics literature has developed approaches and models that could benefit human population genetics modeling. Indeed, an argument often used against the MR and in favor of the RAO model is that human diversity is low and corresponds to an effective size of approximately 10 000. Assuming a subdivided population as in the MR model would lead to census numbers too low to be compatible with any version of the MR model, which would require humans to be present across the Old World. However, as Eller (2002) showed, the argument would not necessarily hold if one accounted for extinction rates. With an extinction rate of 10%, an Ne of 10 000 could be compatible with census sizes greater than 300 000 under a wide range of conditions. This census size could even be larger if one assumed some level of intragroup inbreeding, as is the case in current human groups. Thus, accounting for extinctions would make the MR model compatible with small Ne values. Even though Eller used a simple demographic model (the infinite island model of Wright which allows every population to be in genetic continuity with every other one), this clearly shows that realistic models including extinctions, inbreeding, and differential migration rates could well add unexpected arguments to an already long debate.
Table 1 Examples of mutation and demographic models used to infer ancient human growth patterns
| Demographical model | Initial conditions | Mutation model | Approach | Marker | |||||
| Stepwise | Exponential | Logistic | Linear | Equil | Other | ISM | |||
| Tajima (1989a) | X | X | ISM | Tajima’s D | DNA | ||||
| Slatkin and Hudson (1991) | X | X | ISM | Mismatch | DNA | ||||
| distribution | |||||||||
| Rogers and Harpending | X | X | ISM | Mismatch | DNA | ||||
| (1992) | distribution | ||||||||
| Kimmel et al. (1998) | X | X | X | X | Mono” + Bottle” | aSSM | Imbalance index | Microsatellites | |
| Reich and Goldstein (1998) | X | X | SSM | Summary statistics | Microsatellites | ||||
| Wilson and Balding (1998) | X | X | SMM | Full likelihood | Linked | ||||
| microsatellites | |||||||||
| Pritchard et al. (1999) | X | X | SSM + cSSM | Rejection algorithm | Linked | ||||
| microsatellites | |||||||||
| Beaumont (2004) | X | X | X | SSM | Full likelihood | Microsatellites | |||
| Storz and Beaumont (2002) | X | X | X | SSM | Full likelihood | Microsatellites | |||
| Marth et al. (2003) | X | X | Bottle” | Mismatch | SNPs | ||||
| distributions | |||||||||
| Currat and Excoffier (2004) | X | X | SpatiaL | ISM | Summary statistics | DNA | |||
ISM: infinite site model, aSSM: asymmetric single step model, cSSM: constrained single step model, SSM: single step model. ” Monomorphic initial conditions. fcBottlenecked population.
The patterns and temporal behavior of genomic diversity is also the focus of ongoing and important research. Indeed, it has long been recognized that demographic events can influence patterns of linkage disequilibrium (LD, the statistical association between alleles from different loci), and hence that strong LD between physically unlinked markers could be the signature of admixture events or bottlenecks (Ardlie et al., 2002; Stumpf and Goldstein, 2003; Chikhi and Bruford, 2005). In the last 20 years, it has become increasingly clear that recombination rates vary enormously in the human genome with recombination hotspots separated by regions of low recombination rates (Nachman, 2003; McVean et al., 2004). It has recently been suggested that this structure is not simply the stochastic result in a model of more or less uniform recombination rate, but rather, corresponds to what has been called the blocklike structure of the human genome (e.g., Jeffreys et al., 2001; Ardlie et al., 2002; Stumpf and Goldstein, 2003). There is currently ongoing debate as to whether blocks exist or not (e.g., Anderson and Slatkin, 2004). But it is clear that the patterns of LD observed in many human data sets could not be explained in a model of exponential expansion, which predicted that LD should not extend much over 3 -5 kb around a particular marker (Kruglyak, 1999). Moreover, recent simulations have shown that the expected pattern of LD blocks is stochastic and that even when simulations explicitly assume an extreme variation in recombination rates, some regions may not exhibit a block-like structure depending on the demographic history of the population of interest (Stumpf and Goldstein, 2003). This led these authors to suggest that populations (and regions of the genome) could go through different stages from preblock through block to postblock structure, in a complex manner in which the variance in recombination rates and the demographic history interact. Since different genomic regions have been analyzed in different populations with varied demographic histories, this issue is likely to be discussed for some years.
4. Conclusion and perspectives
We have tried to present above the general principles underlying the use of genetic data to detect past demographical events and estimate parameters of interest. We have seen that there has been a clear tendency toward incorporating more complexity in demographical and mutational models. Larger data sets including many independent loci are also becoming available to the community. For example, Marth et al. (2003) used data from as many as 500 000 SNPs and concluded for a significant bottleneck signal in humans. These data represent new challenges for population geneticists. Indeed, the potential risk in using SNPs is the ascertainment bias associated to their nonrandom discovery and typing. SNPs are usually detected in small samples and tend, therefore, to present balanced allele frequencies, which is not representative of neutral variation (Wakeley et al., 2001; Marth et al., 2003). Recent studies have tried to account for this sampling bias effect (e.g., Nielsen et al., 2004; Wakeley et al., 2001; Marth et al., 2003) but more research needs to be done. Similarly, the sampling of “populations” has to be improved. For instance, in the Akey et al. (2004) study, it is not clear whether differences between African-Americans and European-Americans actually reflect adaptations. Indeed, simulations show that admixture is expected to increase significance in the tests realized. Akey et al. concluded that their result was contrary to the expectation since African-Americans are admixed. As it happens, present-day Europeans are the result of a significant admixture event during the Neolithic transition (e.g., Chikhi et al., 2002), whereas the admixture level observed in African-Americans is very recent and much more limited. Thus, it could be that differences between the two groups are actually the result of their differing admixture histories.
Another avenue of research currently underexplored is the development of statistical approaches to quantitatively compared models (Burnham and Anderson, 2002). Likelihood theory has been used to compare nested models (e.g., Marth et al., 2003) but still much work needs to be done. Other avenues include the use of genomic patterns of diversity (such as variable recombination rates and block-structure patterns). Data from ancient DNA (assuming that contamination can be avoided) will also need to be incorporated in models that allow for genetic data to be sampled at different times. Ongoing research indicates that it is already possible to do so (e.g., Drummond et al., 2002; Shapiro et al., 2004), but future models will have to incorporate population structure since it would be extremely misleading to assume (rather than infer) a genealogical continuity between present-day people and archaeological samples from the same geographical area. A number of graphical methods such as those introduced by Nee et al. (1995) and further developed by Strimmer and Pybus (2001) and others may represent interesting avenues as a first exploratory step. These authors noted that it is possible to convert rates of coalescent events inferred from reconstructed gene phylogenies into Ne values and display them through time together with the corresponding gene tree (Nee et al., 1995). These “skyline plots”, representing variations of Ne through time since the sample’s MRCA, appear to generate different plots under different types of population size changes (linear versus exponential versus logistic). Thus, they could be used to construct a limited set of alternative models before some of the methods described above are applied to the data. A major limitation is that they require the genealogy to be inferred with little error, which is difficult as we have seen. Another similar approach was used by Polanski et al. (1998) who tried to infer the demographic trajectory of humans (assuming monotonic growth) using mtDNA.
At this stage, we would like to make some cautionary remarks on a number of tree- or network-based methods, which have had great success among archaeologists and molecular biologists, but not so much among population geneticists. Indeed, there appears to be increasing use of such methods to devise complex scenarios, with migrations in multiple directions, back migrations, expansions, and long-distance migrations. Many of these complex scenarios are often constructed using sets of linked markers such as mtDNA or Y chromosome haplotypes. From an evolutionary point of view, such markers behave as single loci (with a number of “independent” alleles). The evidence from approximate and full likelihood analyses, which should theoretically extract close to as much information as possible from the data, suggests that they are providing limited amounts of information, even when few demographic parameters are estimated (e.g., Weiss and von Haeseler, 1998; Pritchard et al., 1999; Chikhi et al., 2001). The problem is that many demographic histories can give rise to the same genealogy, and the same demographic history is compatible with many different genealogies. Simulations have shown that population events and tree nodes are very loosely related (Nichols, 2001). For instance, we noted above with the Pritchard et al. (1999) study that the time at which a population expanded had little to do with the TMRCA. In human studies, the already limited information is further reduced by authors who arbitrarily concentrate on subsets (haplogroups). The geographic distribution of haplogroups is then used to describe a possible pattern of past migrations of human populations (see Article 4, Studies of human genetic history using the Y chromosome, Volume 1 and Article 5, Studies of human genetic history using mtDNA variation, Volume 1). It is not clear what assumptions such methods make and under which scenarios they might “work”. It is possible that they could work if one posited that each movement of populations was involving an initial bottleneck followed by an expansion of population size, so that the genealogy would be constrained to follow the demography, and the pattern not blurred by subsequent drifts or admixture. Although it is feasible that this is an accurate description of human history in some regions, it has thus far not been demonstrated. Genetic data are potentially very useful but they may be much more limited than one would like. When single locus data are used, one should always account for the possibility of a huge variance of the coalescent process, particularly when the underlying demography follows the assumptions of the standard coalescent. In this case, for instance, the variance of the TMRCA is approximately 2.3 * Ne for reasonable sample sizes. This means that independent loci, representing independent draws from the same demographic history, are not expected to have similar gene trees or TMRCA values. However, the stable population case represents an extreme, and other demographic histories, for example, expansion, will yield more similar genealogies among loci. Network-based methods are appealing because they are visual and easy to use, but it should be clear that it has not yet been demonstrated that they could provide statistically sound inferences (e.g., Knowles and Maddison, 2002). Their popularity is largely the result of a lack of credible alternative methods for complex modeling of genetic data. However, as demonstrated in this article, the picture is now changing, and we can look forward to an exciting and challenging era based on parametric modeling of genetic data.
We hope that we have convinced the reader that it is a very exciting period to live in. A period in which the complexity of patterns of genomic diversity and of demographic trajectories of human groups is still to be discovered and explored. The field of human population genetic modeling provides, in many ways, richer research avenues than we could have imagined 20 or only 10 years ago.