Statistical Interpretation of Evidence/Bayesian Analysis

Introduction

Bayesian analysis of the statistical interpretation of evidence relies on a rule relating the dependencies among uncertain events through conditional probabilities. This rule enables one to determine the value of evidence in the sense of the effect of the evidence on beliefs in an issue, such as the guilt or innocence of a defendant. The underlying ideas can be applied to categorical and continuous data and to personal beliefs. They can be used to ensure a logical structure to the evaluation of more than one item of evidence and to insure that the evidence is correctly interpreted.

Bayes’ Rule

The Bayesian approach to the interpretation of evidence is named after the Reverend Thomas Bayes, a nonconformist preacher of the eighteenth century. He introduced an important rule, Bayes’ rule, which showed how uncertainty about an event R can be changed by the knowledge of another event S:

where P denotes probability and the bar I denotes conditioning. Thus P (R I S) is the probability R occurs, given that S has occurred. Probabilities are values between 0 and 1; 0 corresponds to an event for which it is impossible that it will happen, 1 to an event which is certain to happen. An alternative version is the odds form, where R denotes the complement of R and P(R) = 1 – P(R). Then the odds in favor of R are P(R)/P(R”), denoted O (R) and the odds in favor of R I S are denoted O(R I S). The odds form of Bayes’ rule is then:

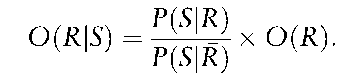
In forensic science, R, S and R can be replaced in the odds form of Bayes’ rule by E, Hp and Hj, where E is the scientific evidence, Hp is the hypothesis proposed by the prosecution and Hj is the hypothesis proposed by the defense.

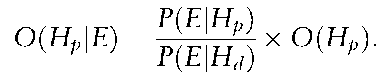
The left-hand-side of the equation is the odds in favor of the prosecution hypothesis after the scientific evidence has been presented. This is known as the posterior odds. The odds O (Hp) are the prior odds (odds prior to the presentation of the evidence). The factor which converts prior odds to posterior odds is the fraction

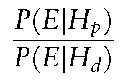
known as the likelihood ratio or Bayes’ factor. Denote this by V, for value. A value greater than one lends support to the prosecution hypothesis Hp and a value less than one lends support to the defense hypothesis Hj. Examples of Hp and Hj include guilt and innocence (G, G), contact or no contact by the suspect with the crime scene (C, C) or, in paternity testing, the alleged father is, or is not, the true father (F, F).
The scientific evidence is evaluated by determining a value for the Bayes’ factor. It is the role of the forensic scientist to evaluate the Bayes’ factor. It is the role of judge and jury to assess the prior and posterior odds. The scientist can assess howthe prior odds are altered by the evidence but cannot assign a value to the prior or posterior odds. In order to assign such a value, all the other evidence in the case has to be considered.
If logarithms are used the relationship becomes additive:

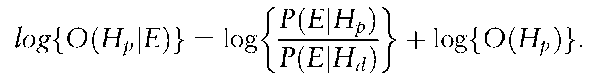
This has the very pleasing intuitive interpretation of weighing evidence in the scales of justice and the logarithm of the Bayes’ factor is known as the weight of evidence. Evidence in support of Hp (for which the Bayes’ factor is greater than 1) will provide a positive value for the logarithm of the Bayes’ factor and tilt the scales in a direction towards finding for Hp. Conversely, evidence in support of Hd (for which the Bayes’ factor is less than 1) will provide a negative value for the logarithm of the Bayes’ factor and tilt the scales in a direction towards finding for Hd. Evidence for which the value is 1 is neutral.
There is a difference between evaluation and interpretation. Evaluation is the determination of a value for the Bayes’ factor. Interpretation is the description of the meaning of this value for the court. Both are considered here.
One of the advantages enjoyed by the Bayesian approach to evidence evaluation is the ability to combine so-called objective and subjective probabilities in one formula. Examples of this are given below in the section on transfer and background evidence. The objective probabilities are those obtained by analyses of data. For example, the relative frequencies of blood groups may be considered to give the probabilities that a particular individual, chosen at random from some relevant population (the one to which the criminal is thought to belong), is of a particular blood group. Subjective probabilities may be provided by the forensic scientist and can be thought of as a measure of the scientist’s belief in the particular event under consideration. For example, when considering the transfer of evidence (such as blood or fibers), the scientist will have an opinion as to how likely (probable) it is that the evidence under examination would be transferred during the course of a crime and be recovered. This opinion can be expressed as a probability which represents the strength of the scientist’s belief in the occurrence of the event about which he is testifying. The stronger the belief, the closer to 1 is the probability.
It is the subjective nature of the Bayesian approach which causes most controversy. Courts do not like subjectivity being expressed so explicitly (R v. Adams, 1996: ‘The Bayes’ theorem [rule] might be an appropriate and useful tool for statisticians but it was not appropriate for use in jury trials or as a means to assist the jury in their task.’).
Another advantage of the Bayesian approach is the help it gives for the structuring of evidence. It insures logical consideration of the dependencies among different pieces of evidence. This is exemplified in the approaches based on influence diagrams or causal networks
Some terminology is required. Evidence whose origin is known is designated source evidence; evidence whose origin is unknown is designated receptor evidence. Other names have been suggested such as control, crime, known, questioned, recovered, suspect.

Early Pioneers of Bayesian Ideas

Examples of the early use of Bayesian reasoning in forensic science are found in relation to the Dreyfus’ case. For example:
An effect may be the product of either cause A or cause B. The effect has already been observed: one wants to know the probability that it is the result of cause A; this is the a posteriori probability. But I am not able to calculate this if an accepted convention does not permit me to calculate in advance the a priori probability for the cause producing the effect; I want to speak of the probability of the eventuality, for one who has never before observed the result. (Poincare 1992)

Another quote, in the context of the Dreyfus’ case is

Since it is absolutely impossible for us [the experts] to know the a priori probability, we cannot say: this coincidence proves that the ratio of the forgery’s probability to the inverse probability is a real value. We can only say: following the observation of this coincidence, this ratio becomes X times greater than before the observation. (Darboux et al. 1908)

Evaluation of Evidence Categorical data

A fuller analysis of the Bayes’ factor is given here to illustrate several underlying principles.
Let Hp be that the defendant was at the scene of the crime and that there was contact between the defendant and the scene resulting in the deposit of a bloodstain at the crime scene by the defendant; denote this hypothesis here by C. The defence hypothesis, Hd,is that the defendant was not in contact with the crime scene and hence the bloodstain was deposited by someone else; denote this hypothesis by C. The evidence E has two parts:
• Es: the blood group T of the defendant (source);
• Ec: the blood group T of the crime stain (receptor).
If the crime stain and the defendant had different blood groups then the blood group evidence would not be relevant. Let J denote the background information. This could include evidence concerning the ethnic group of the criminal, for example. The value of the evidence is then

Consider two assumptions:
1. The blood group of the defendant is independent of whether he was at the scene of the crime (C) or not (C) and thus:

2. If the defendant was not at the scene of the crime (C) then the evidence about the blood group of the stain at the crime scene (Ec) is independent of the evidence (Es) about the blood group of the defendant and thus

The above argument conditions on the blood group of the defendant. A similar argument, conditioning on the blood group of the crime stain shows that

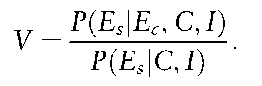
Let the frequency of T in the relevant population be y. Assume the defendant is the criminal: the probability the crime stain is of group T, given the defendant is the criminal and is of group T is 1. Thus, the numerator of V is 1. If the defendant is not the criminal, then the probability the crime stain is of group T is just the frequency of T in the relevant population which is y. Thus the denominator of V is y. The value of the blood grouping evidence is then

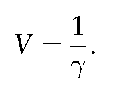
As a numerical example, consider T to be the group AB in the OAB system with frequency y = 0.04 in the relevant population. Then V =1/0.04 = 25. The evidence is said to be 25 times more likely if the suspect were present at the crime scene than if he were not.
If the size of the population to which the criminal belongs (the relevant population) is (N + 1), the prior odds in favor of the suspect equal 1/N, assuming no evidence which favors any individual or group of individuals over any other, and the posterior odds in favor of the suspect equal 1/(Ny).
There is a more general result. Let 7i0 = P(C I J). For each of the other members of the population, let ni be the probability that the ith member left the stain (i = 1, N). Then

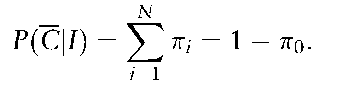
Let pi denote the probability that the blood group of the ith person matches that of the crime stain: i.e. P(EclEs, C, J)= pi, and let wi = Ti/T0. Then

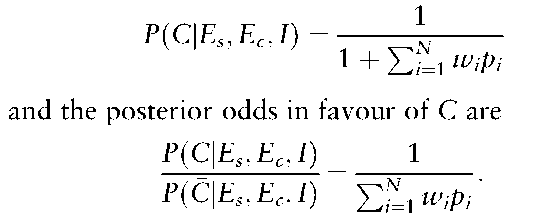
If all of the Wi equal 1 and all of the pi equal y then the posterior odds are 1/(Ny) as before. The more general formulae for the posterior probability and odds can be used to account for evidence that the suspect has a relative, such as a brother, who has not been eliminated from the inquiry.
There are occasions when the numerator of the Bayes’ factor is not 1. Consider an example where a crime has been committed by two people, each of whom has left a bloodstain at the scene. One stain is of group T1, the other is of group T2. A suspect is identified (for reasons unconnected with the blood evidence) and his blood is found to be of group T1. The frequencies of these blood groups are y1 and y2, respectively. The two hypotheses to be considered are
• C: the crime stains came from the suspect and one other person;
• C: the crime stains came from two other people.
The blood evidence E is
• the blood group (T1) of the suspect, (Es, source);
• the two crime stains of groups T1 and T2,(Ec, receptor).
Consider the numerator P(EC I Es, C, J)of V. The stain of group r1 came from the suspect since C is assumed true. Thus, the numerator is y2, the frequency of the other stain, the source of which is unknown. Now, consider the denominator P(EC I Es, C, I)of V. There are two criminals, of whom the suspect is not one. Denote these criminals A and B. Then either A is of group r1 and B is of group T2 or B is of group T1 and A is of group r2. These two events are mutually exclusive and both have probability y1y2. The probability of one event happening or the other, the denominator of V, is their sum, which is 2y1y2. The ratio of the numerator to the denominator gives the value of V as

Compare this result with the single sample case. The value in the two-sample case is one half of that in the corresponding single sample case. This is reasonable. If there are two criminals and only one suspect, it is not to be expected that the evidence will be as valuable as in the case in which there is one criminal and one suspect. These ideas have been extended to cases in which there are general numbers of stains, groups and offenders.

Continuous data

A pioneering paper in 1977 by Dennis Lindley showed how the Bayes’ factor could be used to evaluate evidence which was continuous data in the form of measurements. The measurements used by Lindley by way of illustration were those of the refractive index of glass. There were two sources of variation in such measurements, the variation within a window and the variation between different windows. Lindley showed how these two sources of variation could be accounted for in a single statistic. He was also able to account for the two factors which are of importance to a forensic scientist:
• the similarity between the source and receptor evidence;
• the typicality of any perceived similarity.
Normally, the prosecution will try to show that the source and receptor evidence have the same source, the defence will try to show they have different sources. Before Lindley’s paper evidence had been evaluated in a two-stage process, comparison and typicality:
• are the source evidence and the receptor evidence similar – yes or no? (the comparison stage);
• if no, then assume they come from different sources; if yes, then determine the probability of similarity if the two pieces of evidence came from different sources (the assessment of typicality).
Interpretation is difficult. A small value for the probability of similarity if the two pieces of evidence come from different sources is taken to imply they come from the same source, which is fallacious reasoning, similar to that in the prosecutor’s fallacy discussed below. Also, there is a cut-off point. Pieces of evidence whose measurements fall on one side of this point are deemed ‘similar’ and an assessment of the degree of similarity is made. Pieces whose measurements fall on the other side are deemed ‘dissimilar’ and it is assumed that they come from different sources. Lindley’s approach achieves a continuous gradation from very similar to very dissimilar and encompasses these two stages into one formula. The formula has two components; one accounts for the comparison stage and one accounts for the assessment of typicality. Further developments of Lindley’s approach have followed.
When the data are in the form of measurements the Bayes’ factor is a ratio of probability density functions, rather than a ratio of probabilities.
Consider a set x of source measurements and another set y of receptor measurements of a particular characteristic, such as the refractive index of glass. For this example x would be a set of measurements of refractive indices on fragments of a broken window at the crime scene (source evidence) and y a set of measurements of refractive indices on fragments of glass found on a suspect (receptor evidence). If the suspect was at the crime scene then the fragments found on him could have come from the window at the crime scene, if he was not there then the fragments have come from some other, unknown, source. In general, the characteristic of interest may be parameterized, for example by the mean. Denote the parameter by 9. This parameter 9 may vary from source (window) to source (another window). The evidence of the measurements is E = (x, y). The measurements x are from a distribution with parameter 91, say and the measurements y are from a distribution with parameter 92, say. If x and y come from the same source, then 91 = 92. In practice, the parameter 9 is not known and the analysis is done with the marginal probability densities of x and y. As before, consider two hypotheses
• C: the suspect was present at the crime scene;
• C: the suspect was not present at the crime scene.
Continuous measurements are being considered so the probabilities P of the previous section are replaced by probability density functions f. Then, the value V of the evidence is given by

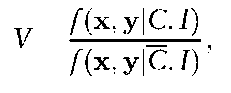
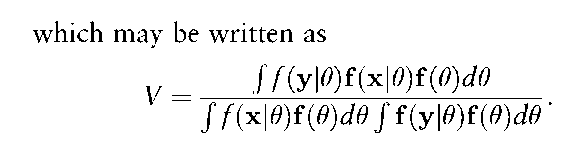
Often, the distributions of (x I 9) and (y I 9) are assumed to be Normal, with 9 representing the mean, varying from source to source, and the variance is assumed to be constant from source to source. Various possibilities have been assumed for the distribution of 9 (with probability density function f(9) which represents the variability among different sources. These include the Normal distribution or some estimation procedure such as kernel density estimation. Further developments are possible involving multivariate data.

Principles

Four principles arise from the application of these ideas.
First, population data need to exist in order to determine objective probabilities. For categorical data, such as blood groups, data are needed in order to knowthe frequency of a particular blood group. For measurement data, such as the refractive index of glass, data are needed in order to model the distribution of measurements, both within and between sources. This requirement for population data means that one needs to have a clear definition of the relevant population. The relevant population is determined by the hypothesis put forward by the defense concerning the circumstances of the crime and by the background information J. It is not necessarily defined by the circumstances of the suspect.
The second principle is that the distribution of the data has to be considered under two hypotheses, that of the prosecution and that of the defense.
The third principle is that evaluation is based on consideration of probabilities of the evidence, given a particular issue is assumed true.
The fourth principle is that the evaluation and interpretation of the evidence has to be conditional on the background information J.

Incorporation of Subjective Probabilities

Another advantage of the Bayesian approach is the ability to incorporate consideration of uncertain events, for which subjective probabilities of occurrence are required. Consider the assessment of the transfer and the presence of background material, innocently acquired.
A crime has been committed during which the blood of a victim has been shed. The victim’s blood group (source evidence) is of group T. A suspect has been identified. A single bloodstain (receptor evidence) of group T is found on an item of the suspect’s clothing. The suspect’s blood group is not T. There are two possibilities: (A0) the bloodstain on the suspect’s clothing has come from some innocent source or (A1) the bloodstain has been transferred during the commission of the crime. The hypotheses to consider are
• C: the suspect and victim were in contact;
• C the suspect and victim were not in contact.
Some additional probabilities are defined. These are t0 = P(A0 I C)and t1 = P(A1 I C), which denote the probabilities of no stain or one stain being transferred during the course of the contact. Also, let b0 and b1 denote the probabilities that a person from the relevant population will have zero bloodstains or one bloodstain on his clothing for innocent reasons. Let y denote the frequency of blood group T in the relevant population. Then, it can be shown that

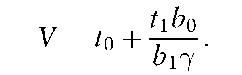
The probabilities t0, t1, b0 and b1 are subjective probabilities, values for which are a matter of the forensic scientist’s personal judgment. The probability y is an objective probability, determined from examination of a sample from a relevant population and the determination from the sample of the relative frequency of group T in the population. The Bayesian approach enables these two different sorts of probabilities to be combined in a meaningful way. Without consideration of transfer and background probabilities, V would be equal to 1/y.

Combining Evidence

The representation of the value of the evidence as a Bayes’ factor enables successive pieces of evidence to be evaluated sequentially. The posterior odds from one piece of evidence, E1 say, become the prior odds for the next piece of evidence, E2 say. Thus

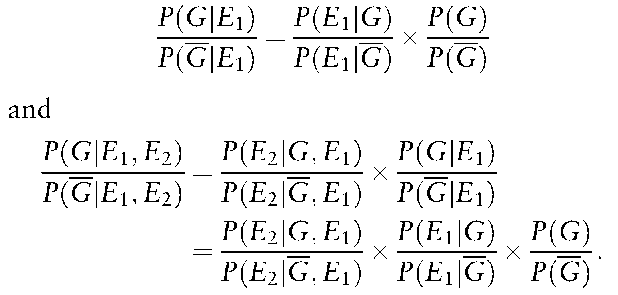
The possible dependence of E2 on E1 is recognized in the form of probability statements within the Bayes’ factor. If the two pieces of evidence are independent this leads to the Bayes’ factors combining by simple multiplication:

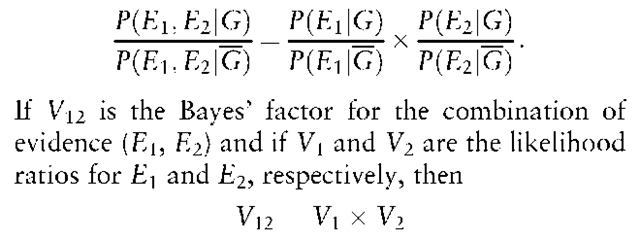
If the weights of evidence (logarithms) are used different pieces of evidence may be combined by addition.
Bayesian analyses can also help to structure evidence when there are many pieces of evidence. This may be done using so-called influence diagrams or causal networks (Fig. 1). Influence diagrams represent the associations among characteristics (individual pieces of evidence) and suspects by a system of nodes and edges. Each characteristic or suspect is represented by a node. Causal connections are the edges of the diagram. Three stages may be considered. These are the qualitative representations of relationships as an influence diagram, quantitative expression of subjective beliefs as probabilities, and coherent evidence propagation through the diagram. Figure 1 represents the relationships in a hypothetical example where there are two suspects X and Y for the murder of a victim V and several pieces of evidence. There is eyewitness evidence E, fiber evidence F, and evidence that Y drives X’s car regularly. T is a suggestion that Y picks up fibers from X’s jacket.
Influence diagrams may be more of an investigatory tool than evidence as they can enable investigators to structure their investigation. A diagram can be constructed at the beginning of an investigation. Nodes can represent evidence that may or may not be found based on previous experience of similar crimes. The edges represent possible associations. Probabilities represent the levels of uncertainty attached to these associations. As evidence is discovered so the nodes and edges may be deleted or inserted. One would then hope that the belief in the guilt or innocence of suspects may become clearer as the probabilities associated with their nodes tend towards one or zero.

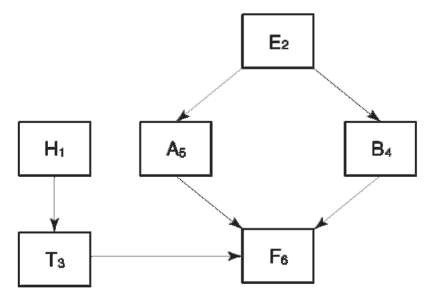
Figure 1 Causal network of nodes in the fictitious example. A: X committed the murder; B: Y committed the murder; E: Eyewitness evidence of a row between X, Y and the victim sometime before the commission of the crime; F: Fibers from a jacket similar to one found in the possession of X are found at the crime scene; H: Y drives X’s car regularly; and T: Y picks up fibers from X’s jacket.

Qualitative Scales

Qualitative scales are intended to make it easier to convey the meaning of the numerical value of the evidence. One such scale has four points:

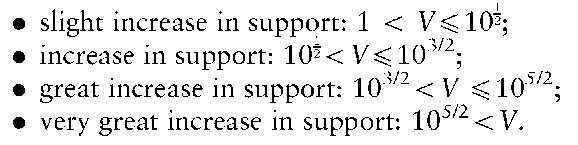
Such a scale is not sufficient to allow for the large values associated with DNA profiling, for example. A scale with more points on it and larger numerical values is more appropriate. This can be made manageable by the use of logarithms.

Interpretation

The Bayesian approach to the interpretation of evidence enables various errors and fallacies to be exposed. The most well-known of these are the prosecutor’s and defender’s fallacies. For example, a crime is committed. A bloodstain is found at the scene and it is established that it has come from the criminal. The stain is of a group which is present in only 1% of the population. It is also estimated that the size of the relevant population is 200 000. A suspect is identified by other means and his blood is found to be of the same group as that found at the crime scene.
The prosecutor argues that, since the blood group is present in only 1% of the population, there is only a 1% chance the suspect is innocent. There is a 99% chance he is guilty.
The defence attorney argues that, since 1% of 200 000 is 2000, the suspect is only one person in 2000. There is a probability of 1/2000 that he is guilty. Thus, the evidence of the blood group is not relevant to the case.
Consideration of the odds form of Bayes’ rule explains these fallacies. Denote the blood type evidence by E. Let the two hypotheses be
• G: the suspect is guilty;
• G: the suspect is innocent.
Then the odds form of Bayes’ rule is that

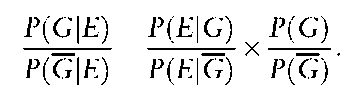
The Bayes’ factor P(E I G)/P(E I G) = 1/0.01 = 100. The posterior odds are larger than the prior odds by a factor of 100.
Consider the prosecutor’s statement. He has said that the probability of guilt, after presentation of the evidence, is 0.99. In symbols, Pr(G I E) = 0.99 and, hence, Pr(G I E) = 0.01. The posterior odds are 99, which is approximately 100. V is also 100. Thus, the prior odds are 1 and Pr(G)=Pr(G) = 0.5. For the prosecutor’s fallacy to be correct the prior belief is that the suspect is just as likely to be guilty as innocent. In a criminal court, this is not compatible with a belief in innocence until proven guilty.
The phrase ‘innocent until proven guilty’ does not mean that P(G) = 0. If that were the case, the odds form of Bayes’ rule shows that, no matter how much evidence was led to support a hypothesis of guilt, P( G I E) will remain equal to zero. Any person who believed that is unlikely to be permitted to sit on a jury.
The defense argues that the posterior probability of guilty P(G I E) equals 1/2000 and, hence, P(G I E) equals 1999/2000. The posterior odds are 1/1999, which is approximately 1/2000. Since the posterior odds are bigger by a factor of 100 than the prior odds, the prior odds are 1/200 000, or the reciprocal of the population size. The defense is arguing that the prior belief in guilt is approximately 1/200 000. This could be expressed as a belief that the suspect is just as likely to be guilty as anyone else in the relevant population. This seems a perfectly reasonable definition of ‘innocent until proven guilty’. The fallacy arises because the defense then argues that the evidence is not relevant. However, before the evidence was led, the suspect was one of 200 000 people, after the evidence was led he is only one of 2000 people. Evidence which reduces the size of the pool of potential criminals by a factor of 100 is surely relevant.
Other errors have been identified. The ultimate issue error is another name for the prosecutor’s fallacy. It confuses the probability of the evidence if a defendant is innocent with the probability he is innocent, given the evidence. The ultimate issue is the issue proposed by the prosecution of which it is asking the court to find in favor. The source probability error is to claim the defendant is the source of the evidence. This would place the defendant at the scene of the crime but would not, in itself, be enough to show that he was guilty. The probability (another match) error assigns the relative frequency of a characteristic to the probability that another person has this characteristic. The numerical conversion error equates the reciprocal of the relative frequency to the number of people that have to be examined before another person with the same characteristic is found.
High values for the evidence provide strong support for the prosecution evidence. They are not sufficient in themselves to declare a defendant guilty. The prior odds have to be considered. Very high values for the evidence, when combined with very small values for prior odds, may produce small values for the posterior odds.