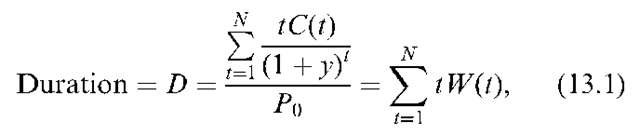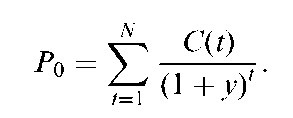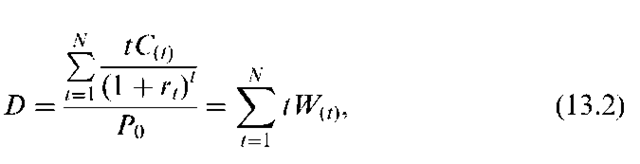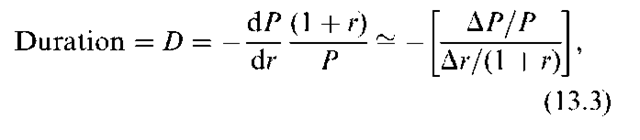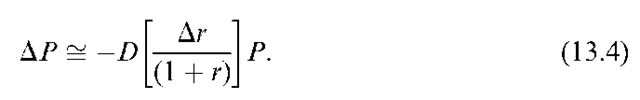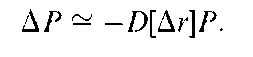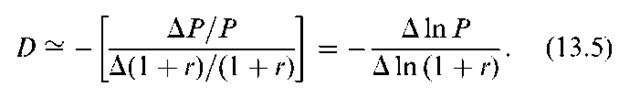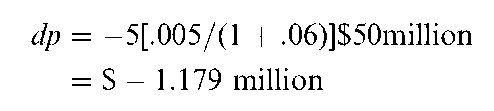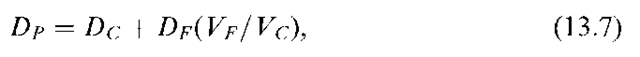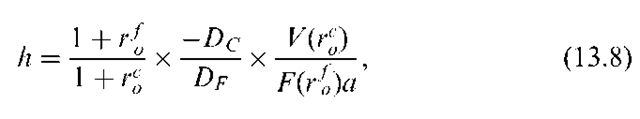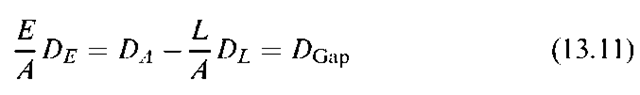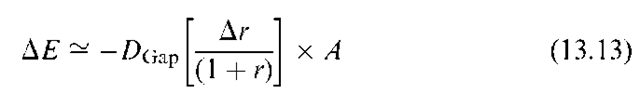Abstract
We discuss duration and its development, placing particular emphasis on various applications. The survey begins by introducing duration and showing how traders and portfolio managers use this measure in speculative and hedging strategies. We then turn to convexity, a complication arising from relaxing the linearity assumption in duration. Next, we present immunization – a hedging strategy based on duration. The article goes on to examine stochastic process risk and duration extensions, which address it. We then examine the track record of duration and how the measure applies to financial futures. The discussion then turns to macrohedging the entire balance sheet of a financial institution. We develop a theoretical framework for duration gaps and apply it, in turn, to banks, life insurance companies, and defined benefit pension plans.
Introduction
Duration Analysis is the key to understanding the returns on fixed-income securities. Duration is also central to measuring risk exposures in fixed-income positions.
The concept of duration was first developed by Macaulay (1938). Thereafter, it was occasionally used in some applications by economists (Hicks, 1939; Samuelson, 1945), and actuaries (Redington, 1952). However, by and large, this concept remained dormant until 1971 when Fisher and Weil illustrated that duration could be used to design a bond portfolio that is immunized against interest rate risk. Today, duration is widely used in financial markets.
We discuss duration and its development, placing particular emphasis on various applications. The survey begins by introducing duration and showing how traders and portfolio managers use this measure in speculative and hedging strategies. We then turn to convexity, a complication arising from relaxing the linearity assumption in duration. Next, we present immunization – a hedging strategy based on duration. The article goes on to examine stochastic process risk and duration extensions, which address it. We then examine the track record of duration and how the measure applies to financial futures. The discussion then turns to macrohedging the entire balance sheet of a financial institution. We develop a theoretical framework for duration gaps and apply it, in turn, to banks, life insurance companies and defined benefit pension plans.
Calculating Duration
Recognising that term-to-maturity of a bond was not an appropriate measure of its actual life, Macaulay (1938) invented the concept of duration as the true measure of a bond’s ”longness,” and applied the concept to asset/liability management of life insurance companies.
Thus, duration represents a measure of the time dimension of a bond or other fixed-income security. The formula calculates a weighted average of the time horizons at which the cash flows from a fixed-income security are received. Each time horizon’s weight is the percentage of the total present value of the bond (bond price) paid at that time. These weights add up to 1. Macaulay duration uses the bond’s yield to maturity to calculate the present values.
where C(t) = cash flow received at time t, W(t) = weight attached to time t, cashflow, X^t=i W(t) = 1, y = yield-to-maturity, and P0 = current price of the bond,
A bond’s duration increases with maturity but it is shorter than maturity unless the bond is a zero-coupon bond (in which case it is equal to maturity). The coupon rate also affects duration. This is because a bond with a higher coupon rate pays a greater percentage of its present value prior to maturity. Such a bond has greater weights on coupon payments, and hence a shorter duration.
Using yield to maturity to obtain duration implies that interest rates are the same for all maturities (a flat-term structure). Fisher and Weil (1971) reformulated duration using a more general (non-flat) term structure, and showed that duration can be used to immunize a portfolio of fixed-income securities.
where rt = discount rate for cashflows received at time t.
Their development marks the beginning of a broader application to active and passive fixed-income investment strategies, which came in the 1970s as managers looked for new tools to address the sharply increased volatility of interest rates.1 In general, duration has two practical properties.
1 Duration represents the ”elasticity” of a bond’s price with respect to the discount factor (1 + y)”1. This was first developed by Hicks (1939). This property has applications for active bond portfolio strategies and evaluating ”value at risk.”
2 When duration is maintained equal to the time remaining in an investment planning horizon, promised portfolio return is immunized.
Duration and Price Volatility
In analyzing a series of cash flows, Hicks (1939) calculated the elasticity of the series with respect to the discount factor, which resulted in re-deriving Macaulay duration. toting that this elasticity was defined in terms of time, he called it ”average period,” and showed that the relative price of two series of cash flows with the same average period is unaffected by changes in interest rates. Hicks’ work brings our attention to a key mathematical property of duration. ”The price elasticity of a bond in response to a small change in its yield to maturity is proportional to duration.” Following the essence of work by Hopewell and Kaufman (1973), we can approximate the elasticity as:
where P denotes the price of the bond and r denotes the market yield. Rearranging the term we obtain:
When interest rates are continuously compounded, Equation (13.4) turns to:
This means that if interest rates fall (rise) slightly, the price increases (decreases) in different bonds are proportional to duration.
The intuition here is straightforward: if a bond has a longer duration because a greater portion of its cash flows are being deferred further into the future, then a change in the discount factor has a greater effect on its price. Note again that, here, we are using yield instead of term structure, and thus strictly speaking, assuming a flat-term structure.
The link between bond duration and price volatility has important practical applications in trading, portfolio management, and managing risk positions. For the trader taking a view on the movement of market yields, duration provides a measure of volatility or potential gains. Other things equal, the trader will seek maximum returns to a rate anticipation strategy by taking long or short positions in high-duration bonds. For derivative strategies, price sensitivity for options and futures contracts on bonds also depends on duration. In contrast with traders, bond portfolio managers have longer horizons. They remain invested in bonds, but lengthen or shorten portfolio average duration depending on their forecast for rates.
Convexity – A Duration Complication
Equation (13.4) is accurate for small shifts in yields. In practice, more dramatic shifts in rates sometimes occur. For example, in its unsuccessful attempt to maintain the U.K. pound in the European monetary snake, the Bank of England raised its discount rate by 500 basis points in one day! In cases where interest rate changes involve such large shifts, the price changes predicted from the duration formula are only approximations. The cause of the divergence is convexity. To understand this argument better, note that the duration derived in Equation (13.3) can be rewritten as:
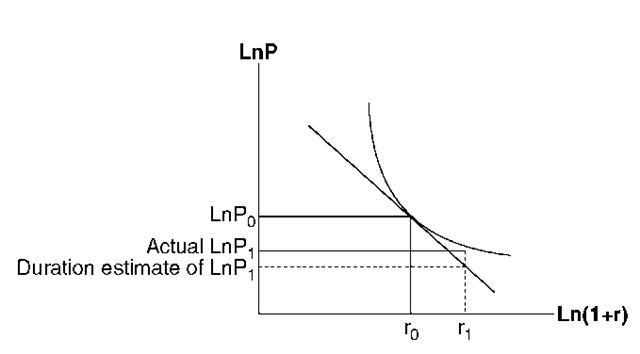
However, the true relationship between lnP and ln (1 + r) is represented by a convex function. Duration is the absolute value of the slope of a line, which is tangent to the curve representing this true relationship. A curve may be approximated by a tangent line only around the point of tangency.
Figure 13.1 illustrates convexity plotting the ”natural log of bond price” on the y-axis and the ”natural log of 1 plus interest rate” on the x-axis. The absolute value of the slope of the straight line that is tangent to the actual relationship between price and interest rate at the present interest rate represents the duration. Figure 13.1 shows that the duration model gives very accurate approximations of percentage price changes for small shifts in yields. As the yield shifts become larger, the approximation becomes less accurate and the error increases. Duration overestimates the price decline resulting from an interest rate hike and underestimates the price increase caused by a decline in yields. This error is caused by the convexity of the curve representing the true relationship.
Figure 13.1. Actual versus duration estimate for changes in the bond price
Thus, convexity (sometimes called positive convexity) is ”good news” for an investor with a long position: when rates fall, the true price gain (along the curve ) is greater than predicted by the duration line. On the other hand, when rates rise, the true percentage loss is smaller than predicted by the duration line.
Note that the linear price-change relationship ignores the impact of interest rate changes on duration. In reality, duration is a function of the level of rates because the weights in the duration formula all depend on bond yield. Duration falls (rises) when rates rise (fall) because a higher discount rate lowers the weights for cash flows far into the future. These changes in duration cause the actual price-change curve to lie above the tangent line in Figure 13.1. The positive convexity described here characterizes all fixed-income securities which do not have embedded options such as call or put features on bonds, or prepayment, or lock-in features in mortgages.
Embedded options can cause negative convexity. This property is potentially dangerous as it reverses the ”good news” feature of positive convexity, as actual price falls below the level predicted by duration alone.
Value At Risk
Financial institutions face market risk as a result of the actions of the trader and the portfolio manager. Market risk occurs when rates move opposite to the forecast on which an active strategy is based. For example, a trader may go short and will lose money if rates fall. In contrast, a portfolio manager at the same financial institution may take a long position with higher duration, and will face losses if rates rise.
Value at risk methodology makes use of Equation (13.4) to calculate the institution’s loss exposure2. For example, suppose that the net position of the trader and the portfolio manager is $50 million (P = $50 million) in a portfolio with a duration of 5 years. Suppose further that the worst-case scenario is that rates, currently at 6 percent, jump by 50
agement professional calculates the maximum loss or value at risk as:
If this maximum loss falls within the institution’s guidelines, the trader and the portfolio manager may not take any action. If, however, the risk is excessive, the treasury professional will examine strategies to hedge the interest rate risk faced by the institution. This leads to the role of duration in hedging.
Duration and Immunization
Duration hedging or immunization draws on a second key mathematical property. ”By maintaining portfolio duration equal to the amount of time remaining in a planning horizon, the investment manager can immunize locking in the original promised return on the portfolio.” Note that immunization seeks to tie the promised return, not to beat it. Because it requires no view of future interest rates, immunization is a passive strategy. It may be particularly attractive when interest rates are volatile.3
Early versions of immunization theory were offered by Samuelson (1945) and Redington (1952). Fisher and Weil (1971) point out that the flat-term structure assumption made by Redington and implied in Macaulay duration is unrealistic. They assume a more general (nonflat) term structure of continuously compounded interest rates and a stochastic process for interest rates that is consistent with an additive shift, and prove that ”a bond portfolio is immune to interest rate shifts, if its duration is maintained equal to the investor’s remaining holding horizon.”
The intuition behind immunization is clearly explained by Bierwag (1987a, Chapter 4). For investors with a fixed-planning period, the return realized on their portfolio of fixed-income securities could be different than the return they expected at the time of investment, as a result of interest rate shifts. The realized rate of return has two components: interest accumulated from reinvestment of coupon income and the capital gain or loss at the end of the planning period. The two components impact the realized rate of return in opposite directions, and do not necessarily cancel one another. Which component dominates depends on the relationship between portfolio duration and the length of the planning horizon. When the portfolio duration is longer than the length of the planning period, capital gains or losses will dominate the effect of reinvestment return. This means that the realized return will be less (greater) than promised return if the rates rise (fall). If the portfolio duration is less than the length of the planning period, the effect of reinvestment return will dominate the effect of capital gains or losses. In this case, the realized return will be less (greater) than promised return if the rates fall (rise). Finally, when the portfolio duration is exactly equal to the length of the planning period, the portfolio is immunized and the realized return will never fall below that promised rate of return.4
Zero-coupon bonds and duration matching with coupon bonds are two ways of immunizing interest rate risk. Duration matching effectively creates synthetic zero-coupon bonds. Equating duration to the planed investment horizon can easily be achieved with a two-bond portfolio. The duration of such a portfolio is equal to the weighted average of the durations of the two bonds that form the portfolio as shown in Equation (13.6).
where W2 = 1 — W1. Setting the right-hand side of Equation (13.6) equal to the investment horizon, this problem is reduced to solving one equation with one unknown.
The preceding argument is consistent with the view presented in Bierwag and Khang (1979) that immunization strategy is a maxmin strategy: it maximizes the minimum return that can be obtained from a bond portfolio. Prisman (1986) broadens this view by examining the relationship between a duration strategy, an immunization strategy, and a maxmin strategy. He concludes that, for a duration strategy to be able to maximize the lower bound to the terminal value of the bond portfolio, there must be constraints on the bonds to be included.
Contingent Immunization
Since duration is used in both active and passive bond portfolio management, it can also be used for a middle-of-the-road approach. Here fund managers strive to obtain returns in excess of what is possible by immunization, at the same time, they try to limit possible loss from incorrect anticipation of interest rate changes. In this approach, called contingent immunization, the investor sets a minimum acceptable Holding Period Return (HPR) below the promised rate, and then follows an active strategy in order to enhance the HPR beyond the promised return. The investor continues with the active strategy unless, as a result of errors in forecasting, the value of the portfolio reduces to the point where any further decline will result in an HPR below the minimum limit for the return. At this point, the investor changes from an active to immunizing strategy5.
Stochastic Process Risk – Immunization Complication
Macaulay duration uses yield to maturity as the discount rate as in Equation (13.1). Because yield to maturity discounts all bond cash flows at an identical rate, Macaulay duration implicitly assumes that the interest rates are generated by a stochastic process in which a flat-term structure shifts randomly in a parallel fashion so that “all” interest rates change by the same amount. When we assume a different stochastic process, we obtain a duration measure different from Macaulay duration (Bierwag, 1977; Bierwag et al., 1982a). If the actual stochastic process is different from what we assume in obtaining our duration measure, our computed duration will not truly represent the portfolio’s risk. In this case, equating the duration measure to the investment horizon will not immunize portfolio, and there will be stochastic process risk. Although immunization is a passive strategy, which is not based on an interest rate forecast, it is necessary to predict the stochastic process governing interest rate movements.
A number of researchers have developed strategies for minimizing stochastic process risk and its consequences (for example, Fong and Vasicek, 1983, 1984; Bierwag et al., 1987, 1993; Prisman and Shores, 1988; Fooladi and Roberts, 1992).
In a related criticism of Macaulay duration, Ingersoll et al. (1978) argue that the assumed stochastic process in the development of single-factor duration models is inconsistent with equilibrium conditions. The source of arbitrage opportunities is the convexity of the holding period return from immunized portfolios with respect to interest rate shifts. Total value is a convex function of interest rate changes, which for the immunized funds has its minimum at the point of the original rate, r0. This means that holding period return is also a convex function of interest rate shifts with the minimum at the original rate. Thus, the larger the shift, the greater the benefit from an interest rate shock. Therefore, in particular in the presence of large shocks to interest rates, and or for high-coupon bonds, risk-less arbitrage would be possible by investors who short zero-coupon bonds for a return of r0, and invest in other bond portfolios without taking an extra risk.
Although, this argument is sound, it does not mar the validity of immunization strategies. Bier-wag et al. (1982a) develop an additive stochastic process that is consistent with general equilibrium, and for which the holding period return is not a strictly convex function of interest rate shifts. Further, Bierwag (1987b) shows that there is no one-to-one correspondence between a particular duration measure and its underlying stochastic process. Duration measures derived from some disequilibrium processes such as the Fisher-Weil process, the Khang process, and additive and multiplicative processes of Bierwag also correspond to equilibrium processes. Additionally, Bierwag and Roberts (1990) found examples of equilibrium stochastic processes give rise to duration measures that have been previously derived from disequilibrium stochastic processes such as Fisher-Weil duration.
On the practical side, the risk-less-arbitrage argument seemed hypothetical to many practitioners who were aware of the difficulties in taking a large short position in bonds. Practitioners were more concerned that the reality of nonparallel shifts in sloping yield curves could impair the hedges constructed based on Macaulay duration.
The current generation of models incorporates the term structure so that it is no longer the case that duration users must assume a flat-term structure. Bierwag et al. (1983b, 1987, 1993) and Bren-nan and Schwartz (1983) are a few examples. Current models also allow for nonparallel shifts in the yield curve. These include multifactor models (Chambers et al., 1988; Nawalka and Chambers, 1997) in which the short and long ends of the yield curve are allowed to shift in opposite directions.6
Effectiveness of Duration-Matched Strategies
Given that duration extensions are numerous, how effective is basic Macaulay duration in the design and implementation of active and passive strategies? Bierwag and Roberts (1990) test the key implication of duration theory for active managers – portfolios with higher durations are predicted to have greater price sensitivity when rates change. Constructing portfolios with constant durations using Government of Canada bonds, they measure monthly holding period returns over the period of 1963-1986. They find that, as predicted, higher duration portfolios had greater return volatility and that Macaulay duration explained around 80 percent of the variance in holding period returns.
A number of studies examine the effectiveness of immunization over sample sets of government bonds for the United States, Canada, and Spain, among others. Fooladi and Roberts (1992) use actual prices for Government of Canada bonds over the period 1963-1986, setting the investment horizon to five years, and rebalancing every six months to maintain duration equal to the time remaining in the investment horizon. Their performance benchmark consists of investing in a bond with maturity matched to the horizon. This maturity-bond strategy involves buying and holding a bond with an initial five year maturity. Due to stochastic process risk, there will always be cases in which the duration hedging strategy falls short or overshoots the promised return, which brings the target proceeds. Their test measures hedging performance so that the better strategy is the one that comes closer most often to the original promised return. They conclude that duration matching allowed the formation of effective hedges that outperformed nonduration-matched portfolios. These results validate the widespread use of Macaulay duration in measuring risk and in immunization. They also support similar results obtained for U.S. Treasury Securities by Bierwag and coworkers (1981, 1982b).
Beyond establishing the credibility of duration matching as a hedging technique, empirical research has also probed the hedging effectiveness of alternative duration-matching strategies in the face of stochastic process risk. Fong and Vasicek (1983, 1984) propose hedging portfolios designed by constraining M-squared, a measure of cashflow dispersion. Prisman and Shores (1988) and Bierwag et al. (1993) show that the Fong-Vasicek measure does not offer a general solution to minimizing hedging error. The latter paper reinforces results in tests of duration effectiveness discussed earlier which find that stochastic process risk is best controlled by constraining the portfolio to include a maturity bond. This result is replicated for immunization in the Spanish government bond market by Soto (2001).
Going beyond Macaulay duration, Soto (2001) and Nawalkha and Chambers (1997), among others, examine the increase in hedging effectiveness offered by multi-factor duration models. They establish that a three-factor model controlling for the level, slope and term structure curvature works best in the absence of the maturity bond constraint.
Use of Financial Futures
The basics of duration analysis can be combined with the use of futures markets instruments for hedging purposes. An investor can hold a long position in a certain security (for example, three month bankers acceptances) and a short position in a futures contract written on that security, and reduce overall exposure to interest rate risk. This is because, as interest rates change, prices of the security and the futures contract move in the same direction and gains and losses in the long and short positions largely cancel out. The durations of the security held long and of the security underlying the futures contract determine the hedge ratio. When we combine the cash and futures positions, the duration of the overall portfolio may be expressed as:
where, DC, DF, and DP denote durations of the cash portfolio, futures portfolio, and the overall portfolio, respectively, and VF and VC are the values of futures and cash positions, respectively. It should be noted that VF = hF where F denotes the futures price and h is the number of future contracts per unit of cash portfolio (the hedge ratio).
Bierwag (1987a) shows that, for a perfect hedge, in general the hedge ratio (h) is determined by:
where V(rco) = the value of the long position, F(rfo) = the future price for one unit of contract, rC = the current yield to maturity of the long asset, r-C = the current yield to maturity of the asset underlying the futures contract, and a = the derivative rf with respect to rc.
If the underlying asset is the same and the maturities of asset and future contract are identical, it may be reasonable to assume a = 1. Equation (13.7) shows how an investor can use futures contracts to alter duration of a bond portfolio.
Duration of Corporate Bonds
Our review of immunization research has so far concentrated on government bonds, and ignored default risk. In practice, bond portfolio managers often hold corporate, state, and municipal bonds to enhance yields. This raises the question of how to apply immunization to such portfolios. Simply using Macaulay (or Fisher-Weil) duration for each bond to find portfolio weights will be misleading. Ignoring default risk is equivalent to assuming that we have locked in a higher yield than is possible immunizing with government bonds alone. The promised return must be adjusted to an expected return reflecting the probability of default.
As Bierwag and Kaufman (1988) argue, in computing duration for nondefault-free bonds, in addition to the stochastic process governing interest rate shifts, we must also consider the stochastic process governing the timing of the losses from default. Default alters both a bond’s cash flows and their timing. Thus, we cannot immunize a portfolio of nonde-fault-free bonds at its promised rate of return. An interesting question follows. Is it possible to immunize such a portfolio at its (lower) risk-adjusted return using a single-factor duration model?
Fooladi et al. (1997) answer affirmatively but contend that Macaulay duration is not a true measure of interest rate sensitivity for bonds with default risk. Assuming risk-averse investors, they derive a general expression for duration, which includes terms for default probabilities, expected repayment, and the timing of repayment. They illustrate that, under certain circumstances, their general single-factor duration measure is an immunizing measure. They conclude that practical application of duration analysis in immunization calls for employing duration measures that are adjusted for default risk.
Jacoby (2003) extends the model of Fooladi et al. (1997), by representing bondholders’ preferences with a log-utility function. Accounting for default risk, his duration measure is the sum of the Fisher-Weil duration and the duration of the expected delay between the time of default and actual recovery caused by the default option. Using historical long-term corporate bond default and recovery rates, he numerically simulates his duration measure. His conclusion is that failing to adjust duration for default is costly for high-yield bonds, but appears to be trivial for investment-grade bonds.
In an earlier paper, Chance (1990) draws on Merton’s (1974) option pricing bond valuation. Chance shows that the duration of a zero-coupon bond is the weighted average of the duration of a corresponding risk-less discount bond and that of the limited liability option. Chance finds that his duration is lower than the bond’s Macaulay duration (maturity for a zero-coupon bond).
Since many corporate bonds are callable, Acharya and Carpenter (2002) also use option pricing technology to derive a valuation framework of callable defaultable bonds. In their model, both interest rates and firm value are stochastic and the call and default decisions are endogenized. With respect to interest rate sensitivity, as in Chance’s model, their model implies that default risk alone reduces the bond’s duration. They further show that, everything else being equal, call-risk will also shorten bond duration.
The theoretical work of Chance (1990) and Acharya and Carpenter (2002) emphasizes the significance of adjusting Macaulay duration for both default and call-risks. Jacoby and Roberts (2003) address the question of the relative importance for duration of these two sources of risk. Using Canadian corporate data, they estimate and compare the default-and call-adjusted duration with its Macaulay counterpart. In general, their results support the need for callability adjustment, but fail to uncover any significant impact of default risk for investment-grade callable and defaultable bonds. Their results provide some support for the Acharya and Carpenter (2002) model, that predicts an interaction between call and default risks. Jacoby and Roberts demonstrate that during a recessionary period (1991-1994), the call adjustment is less important (but still significant) relative to other periods. This is because bond prices are depressed during recessionary periods, and therefore the incentive to call these bonds arising from lower interest rates is significantly reduced.
Macrohedging
This section broadens the application of duration to ”macrohedging” addressing interest rate exposure at the macro level of a corporate entity, in particular, a financial institution. Macrohedging or balance sheet hedging considers the entire balance sheet and treats both sides as variable. Without a macro approach to hedging, we are forced to take the liability side as given, and cannot address asset/liability management.
As with its micro counterpart, macrohedging can be a tool for either passive or active strategies. In a passive (”routine hedging”) strategy, immunization for example, hedging seeks to eliminate interest rate risk completely. In contrast, an active (”selective hedging”) approach leaves some interest rate exposure unhedged seeking to achieve superior returns based on a view of future rates.
Duration Gap
A ”duration gap” measures the mismatch between assets and liabilities. When the duration gap is zero, the assets and liabilities are perfectly matched so that the financial institution’s net worth is immunized against shifts in interest rates. We illustrate duration gap using a simple example involving ”one” discount rate for all assets and a financial institution with a single asset, which is financed partly by equity and partly by liabilities. The balance sheet identity requires:
where A denotes assets, E denotes equity, and L denotes liabilities. Taking the derivative of Equation (13.9) with respect to the interest rate (single discount rate) and rearranging the terms we obtain:
For the equity to be unaffected by changes in interest rates, the right hand side of Equation (13.10) must be zero. Multiplying both sides of Equation (13.10) by a fixed quantity, (1 + r)/A, and noting the definition of duration, we obtain
where DA, DL, and DE denote the durations of assets, liabilities, and equity, respectively. The right hand side of Equation (13.11) is called duration gap, DGap. A zero duration gap tells us that the equity has zero interest rate exposure.
Restating the equation for duration of equity in terms of Equation (13.3), replacing P (for price) with E (for equity), results in Equation (13.12).
Substituting for DE from Equation (13.12) into Equation (13.11), and rearranging the terms results in the following formula for changes in the value of equity as a function of duration gap7:
This highly useful formula shows how a shift in interest rates impacts the market value of an Financial Institution equity.8 It is set up so that duration gap mathematically plays the same role as duration in the corresponding formula for fixed-income securities in Equation (13.4). When duration gap is zero, the shares of the FI will not be affected by interest rate shocks; the Fl’s shares will behave like floating rate bonds with zero duration. The shares of an FI with a positive duration gap will rise when rates fall analogously to a long position in a bond. If an FI has a negative duration gap, its shares will increase in value when rates rise. Holding the shares of such an FI is like taking a short position in a bond.9
It follows that, in parallel with fixed-income securities, the formula (Equation 13.13) has practical implications both for passive management (immunization) and for active management (interest rate speculation). To illustrate, suppose that the management of an FI regards future interest rate movements as highly uncertain. In this case, the FI should immunize by setting the duration gap to zero. On the other hand, if senior executives predict that rates will fall, the FI should expand its portfolio of longer term loans financed by short term deposits increasing DGap.10
Central to this strategy is the implied assumption that the difference between convexity of assets and convexity of liabilities (adjusted for capital structure and the ratio of return on assets over return on liabilities) is non-negative. Fooladi and Roberts (2004) show that if this difference which they call ”convexity gap” is not nonnegative, satisfying duration condition is not sufficient for hedging against interest rate risk.
To reduce adjustment time, and to save on transactions costs, FIs adjust duration gaps using off-balance-sheet positions in derivative securities such as interest rate futures, interest rate options and swaps. Bierwag (1997) shows that to find the proper hedge ratio for futures hedging, we simply substitute DGap for Dc in Equation (13.8) (that is used for constructing hedged positions in bond portfolios).
Other Applications of Duration Gaps
Duration gap also has applications to managing the balance sheets of life insurance companies and pension funds, and even to nonfinancial corporations and governments.
Life insurance companies were the first class of financial institutions to implement duration matching.11 Policy reserves are the main liability of a life company and represent the expected present value of future liabilities under life policies.
The typical life insurance company invests the bulk of its assets in bonds and mortgages. This leads to a constitutionally negative duration gap as future policy liabilities generally have a longer duration than bonds and mortgages. To address the resulting interest rate exposure, during the 1980s life companies increased their investments in mortgages and other positions in real estate. The recession and real estate collapse of the early 1990s led to the insolvency of several life companies. Today, well-managed life insurance companies recognize that off-balance sheet positions in futures and other derivatives offer an attractive way to hedge an imbalanced duration gap without the risks that come with large positions in real estate.
Pension plans come in two types: defined benefit and defined contribution. The balance sheet of a defined benefit pension plan, like that of a life insurance company, has a constitutional imbalance in duration. Given that an average employee may retire 20 years from today, and then live for another 20 years, the duration of the pension liability is generally longer than the duration of the asset portfolio invested in equities and bonds. As a result, in the 1990s, many defined benefit pension plans were increasing their equity exposures and taking equity positions in real estate.12 Bodie (1996) shows that this leaves pension funds exposed to mismatched exposures to interest rate and market risks. Beginning in 2000, sharp declines in both stock prices and long-term interest rates created a ”Perfect Storm” for defined benefit pension funds (Zion and Carache, 2002). As a result, a number of plans are seeking to switch to the defined contribution format.
Many pension plans offer some form of indexation of retirement benefits to compensate for inflation that occurs after employees retire. To address inflation risk, pension funds can immunize all or part of their liabilities against interest rate risk using macro or micro hedging, and then add an inflation hedge. The portfolio shifts to equities and real estate investments discussed earlier offer a potential inflation hedge. Another attractive possibility is Treasury Inflation Protected Securities (TIPS). These bonds offer indexation of principal and interest, and thus have approximately zero nominal (inflation) duration.
Duration gaps can also be used to hedge the equity of nonfinancial corporations and governments against interest rate fluctuations. For example, in a highly innovative application of duration analysis, the New Zealand government explored how this tool could help guide the recent restructuring of its liabilities.13