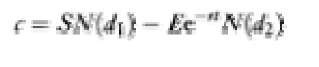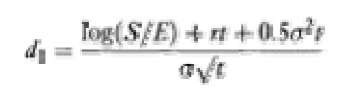This is a famous equation for determining the price of an option, first discovered in 1972 by Fischer Black of Goldman Sachs and Myron Scholes of the University of Chicago and published in Black and Scholes (1973). The unique insight of this research was to use arbitrage in solving the option-pricing problem. Black and Scholes reasoned that a position which involved selling a call option and buying some of the underlying asset could be made risk-free. It would be a hedged position and, as such, should pay the risk free rate on the net investment. Using continuous-time mathematics they were able to solve for the call price from the equation for the hedged position. This resulted in an equation for the value of a European option (i.e. one which cannot be exercised before maturity) which did not need to take account of the attitude to risk of either the buyer or seller.
The equation (expressed for a call option) is:
where c is the call price, S is the asset price, N(x) is a normal-distribution probability, E is the exercise price, r is the interest rate in continuou s form and t is years to maturity.
The N(d1) and N(d2) values, which are probabil ities from the normal-distribution, have values for d and d- calculated as follows:
and
where a is the standard deviation of returns on the asset per annum.
In the equation, the value of a call option depends on five variables: the asset price (S), the exercise price (E), the continuous interest rate (r), the time to maturity (t), and the standard deviation of returns on the asset (a) (which is usually known as the volatility). Of these five variables, only the volatility is unknown and needs to be forecasted to the maturity of the option. The call price in the equation is a weighted function of the asset price (S) and the present value of the exercise price (Ee-t) The weights are respectively N(d) which is the hedge ratio or “delta” of the option, and N(d2) which is the probability that the option matures in the money.
Many academic papers have proposed more complicated models, only to conclude that the simple Black-Scholes model can be modified to give almost equally good results. Several assumptions are necessary to derive the model , but it is surprisingly robust to small changes in them. The first assumption is that the asset price follows a random walk with drift. This means that the asset price is lognormally distributed and so returns on the asset are normally distributed. This assumption is widely used in financial models. The second assumption is that the distribution of returns on the asset has a constant volatility. This assumption is clearly wrong and use of the model depends crucial ly on forecasting volatility for the period to maturity of the option. The third assumption is that there are no transaction costs, so that the proportions of the asset and option in the he dged portfolio may be continuously adjusted without incurring huge costs. This assumption sounds critical, but it is relatively unimportant in liquid markets. The fourth assumption is that interest rates are constant, which is not correct but is of little importance since option prices are not very sensitive to interest rates. The fifth assumption is that there are no d ividends on the asset, which once again is unrealistic, but modification of the model to accommodate them is relatively simple (e.g. Black, 1975).
While most of the theoretical results in finance have not had any impact on practitioners, the Black-Scholes model is universally known and used. The existence of the equation has facilitated the development of markets in options, both on-exchange (beginning with the Chicago Board Options Exchange in 1973) and over the counter. Without the equation, there could not have been such rapid growth in the use of derivative assets over the last twenty years. Many derivative assets might even not exist.