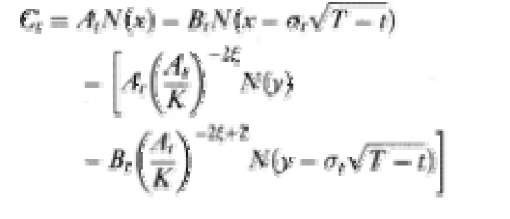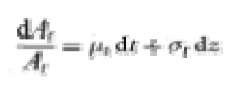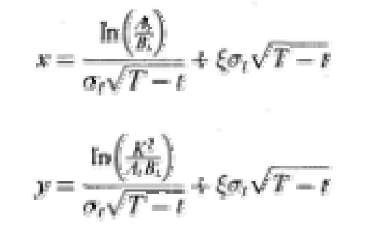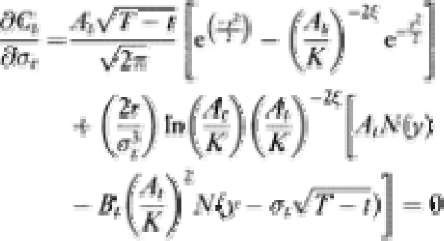A barrier option is an option which is initiated or extinguished if the underlying asset price hits a prespecified value. More specifically, a “down and out call” is a call option expiring worthless as soon as the value of the underlying asset hits a lower bound K, which is usually equal to or less than the option’s exercise price, as developed in Merton (1973) and Cox and Rubinstein (1985).
Chesney and Gibson (1993, 1994) applied the down and out call model to the pricing of equity in a levered firm, while Paris (1995, 1996) extended the model to banks and financial intermediaries.
Valuing bank capital as a traditional call option written on the bank assets, with a strike price equal to the total bank deposits, has two main theoretical underpinnings:
1. As soon as the bank asset value declines to the value of the liabilities, the bank capital is worth zero, while the call value is positive, before the option’s expiration.
2. In order to maximize the market value of their equity, the bank shareholders systematically choose the most risky projects characterizing the investment opportunity set.
The down and out call approach overcomes both of these problems. The value of the bank capital is:
where C, is the current market value of the bank capital, A, is the stochastic current value of the bank assets, which follow a continuous diffusion process,
where p.t is the expected instantaneous rate of return of the bank assets, a, is the standard deviation of the instantaneous rate of return of the bank assets, z is a standard Wiener process, Bt is the current market value of the bank liabi lities, K is the knock out value, assumed to be
and goes to zero whenever At > K.
The optimal value of the asset volatility is ob tained by setting the partial derivative of the capital value with respect to the bank asset volatility equal to 0:
This equation can be solved numerically. The optimal value of the asset volatility is an increasing function of the bank leverage and a decreasing function of the knock-out value K. This result means that the greater the bank’s capitalization, the lower the management bias towards the volatility of its investments.
K can be interpreted as a reputational constraint resulting in insolvency if it is violated. It is usually industry specific, even if it could be related to some firm specific feature, like leverage.
This approach to the valuation of bank capital has two fundamental implications: (1) the asset volatility is related to the bank capital structure , meaning that an explicit and positive linkage exists between the two main sources of risk in the bank; and (2) the existence of an optimal asset volatility implies that the bank shareholders may be risk averse instead of risk neutral, as they are traditionally considered in the theoretical literature, eliminating, as a consequence, any behavioral differences among shareholders and bank managers. Distinguishing between a shareholder and a management-controlled bank is thus meaningless, to the extent that the utility function of the bank controller is considered.
Paris (1995) applies the down and out call framework to the valuation of bank capital. This approach has two merits. (1) The market value of the bank capital can be easily computed at any time, once the marking to the market of bank assets and liabilities is assumed to be feasible, and a continuous time model of bank monitoring can be implemented. It is worthwhile to stress that frequent, possibly continuous, monitoring is a necessary, if not sufficient, condition for prompt and effective corrective actions by financial regulators, in case of bank problems. (2) The chosen optimal value of the bank asset volatility, if observed by the market, is an effective signal of the true bank capitalization. The important implication is that observing the bank’s investment strategy allows the market to evaluate the bank’s safety and soundness.
An extension of the down and out call model to any kind of financial intermediary has been applied in Paris (1996) in order to derive relevant properties of alternative regulatory approaches. Once more the optimal intermediary asset volatility is the critical variable determining the intermediary’s response to the regulatory provision, in addition to the regulator’s action in terms of minimum capital requirement. Moreover, under specific conditions, the same volatility measure can be unambiguously inferred by the market, by simply observing the intermediary’s capital ratio.