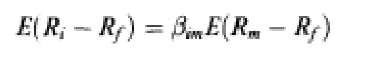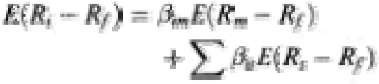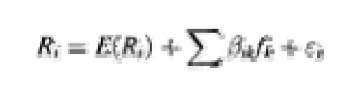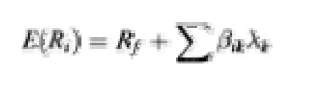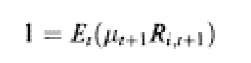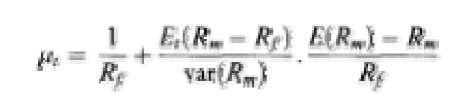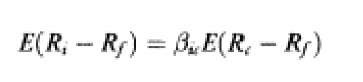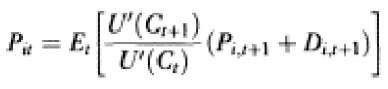The modern theory of asset prices has its foundations in the portfolio selection theory initiated by Markowitz (1952). In a one-period framework Markowitz assumed that agents’ utilities, and hence the price they will pay, depend only on the means and variances of returns. This mean-variance model can be justified either on the grounds of quadratic utility (for arbitrary distributions of the asset returns) or on the grounds of multivariate normal (or, more generally, elliptic) distribution of asset returns (for arbitrary preferences). Although quadratic utility has the unappealing properties of satiation and increasing absolute risk aversion in the sense of Arrow-Pratt and multivariate normality violates the limited liability properties of assets, the mean-variance model has had a perv asive influence on financial economics.
The portfolio frontier obtained within the mean-variance framework can be generated by any two frontier portfolios, a property called two-fund separation. Lintner (1965), Sharpe (1964), and Mossin (1966) combined the two-fund separation with the assumptions that agents have homogeneous beliefs, that markets clear in equilibrium, and that there is unlimited lending and borrowing at the riskless rate. The resulting model, the capital asset pricing model (CAPM), has been the major framework of thinking about the trade-off between risk and return. The (unconditional) CAPM states that the excess return on each asset (return less the risk-free rate) is proportional to the asset’s market beta:
where Rm is the return on the market portfolio and J = cov(Rh R„,)/var(R„,), the asset’s market beta, measures the covariance of the asset’s return with the market return. Black (1972) derived the CAPM for an economy without a ri skless asset (the zero-beta CAPM).
The CAPM has been extensively tested. Black et al. (1972) and Fama and MacBeth (1973) originated the two frameworks in which most of the tests were done. However, the unsatisfactory empirical performance of the CAPM, as well as the problems identified by Roll (1977) related to the unobserved nature of the market portfolio, are the reasons why the single-period, single-beta relation had to be relaxed. Historically, the first direction was to place the individual decision making in an intertemporal set-up in which agents maximized utility, thus leading to the intertemporal CAPM (ICAPM) of Merton (1973). The other is the arbitrage pricing theory (APT) of Ross (1976).
Merton, working in continuous time under th e assumptions of many identical agents with homogeneous expectations and market clearing, derived the ICAPM. The asset prices in Merton’s model follow a diffusion process. If the investment opportunity set, namely the drift and diffusion parameters, and the instantane ous correlations between the returns of the different assets, do not change over time, then a continuous time version of the static CAPM holds: one obtains a single-beta security-market-line relationship. If the investment opportunity set is stochastic, however, a multi-beta relationship emerges:
where ( measures the covariance of the return of the z’th asset with the sth state variable. Thus, with a stochastically changing investment opportunities set agents need to hedge the future changes in their consumption for a given level of wealth. Given the interpretation of the S state variables as portfolios, the S portfolios are often referred to as hedge portfolios.
To derive the arbitrage pricing theory (APT) Ross (1976) assumes that asset returns are generated by a linear factor model:
where each factor f (without loss of generality) and the error s are zero-mean. In well-diversified portfolios the excess expected return on each asset will be given by a linear combination of the (‘s above:
where the (s are referred to as factor loadings while the X’s are the risk premiums.
Huberman (1982) offers an alternative derivati on of the APT. Connor (1984) was the first to use equilibrium arguments in relation to the AP T. Connor and Korajczyk (1986, 1988) extend his arguments. Dybvig and Ross (1983) and Ingersoll (1984) contain useful extensions and refinements of the APT.
There has been substantial empirical work on the APT. Roll and Ross (1980) use factor analysis to test the APT while Connor and Korajczyk (1988) use “asymptotic” principal components analysis to uncover the factors. On the other hand, Chen et al. (1986) explicitly specify five macroeconomic variables (unexpe cted change in the term structure, unexpected change in the risk premium, change in expected inflation, the unexpected inflation rate, and the unexpected change in industrial productio n) that proxy for the economy-wide factors. Shanken (1982, 1985) questions the possibility of testing the APT; Dybvig and Ross (1983) present the counter-argument.
The works of Ross (1976), Cox and Ross (1976), Harrison and Kreps (1979), and Ross (1978) contain what has come to be known as the fundamental theorem of asset pricing: the absence of arbitrage is equivalent to the existence of a positive linear pricing rule and still further equivalent to the existence of an optimal demand for some agent with increasing preferences.
From this theorem it follows that the absence of arbitrage implies the existence of a strictly positive stochastic process called a stochastic discount factor p.t such that:
For the CAPM (an equilibrium model):
while for the consumption CAPM (CCAPM) pt = U’(Ct+l)/U’(C). The theoretical work on both the ICAPM and APT preceded much of the empirical work which found that price-earnings ratios (Basu, 1977), dividend yi elds (Fama and French, 1988), and size (Banz, 1981; Reiganum, 1981; Schwert, 1983; Chan et al., 1985) improve the fit of the single-beta CAPM. Some of these papers, together with the weekend effect (French, 1980) and the January effect (Keim, 1983) have been interpreted as evidence of market inefficiency. However, as Fama (1970) has noted, a test of market efficiency, being performed within the framework of a specific model, is a test of that particular model as well. Much research has been done on whether any of these statistics are proxies for others. Reiganum (1981) has shown that the price-earnings effect disappears when controlling for size. Recently, Fama and French (1992, 1993) have shown that size and topic-to-market equity (portfolios proxying for factors related to size and topic-to-market equity) have high explanatory power for the cross-section (variance) of expected returns.
Considerable work has also been done on testing the conditional CAPM (Sharpe, 1964; Constantinides, 1982). Keim and Stambaugh (1986), among others, have shown that in a CAPM context the risk premium is time varying. Harvey (1989) and Ferson and Harvey (1991) show that the betas are also time varying. These authors have argued that failing to recognize the time variability may lead to a premature rejection of the model.
Historically, the difficulties in identifying the relevant state variables to be used in Merton’s ICAPM have led Breeden (1979) to reduce th e multi-beta model to a single-beta, CCAPM model:
where Rc is the return on a security which is pe rfectly correlated with aggregate consumption and Jic = cov(Ri, d ln C)/var(d ln C).
Lucas (1978) independently derives this asset pricing model in discrete time for a pure exchange economy in which aggregate con sumption equals the aggregate dividend in equilibrium. For that model the price of asset i is a properly discounted sum of next period’s payoff:
where the representative consumer is assumed to maximize a time- and state-separable utility function with periodic utility U(C). Cox et al. (1985a, 1985b) present a full-fledged general equilibrium model (with production) in continuous time along these lines and apply it to a study of the term structure of interest rates. Brock (1982) also derives asset prices in a production economy.
The consumption-based CAPM has not been very successful empirically. The Euler equations have been rejected by Grossman and Shiller (1981), Hansen and Singleton (1982), and Grossman et al. (1987). Moreover, the simple separable utility representative agent model gives rise to various asset pricing puzzle s such as the equity premium puzzle of Mehra and Prescott (1985) and the risk-free rate puzzle of Weil (1989).
Recent work on the consumption-based asset pricing model has focused on the calibration of preferences and investment opportunities to in clude various market frictions (borrowing and short-sales constraints, transactions costs (Bewley, 1992; Heaton and Lucas, 1992)), time non-separable preferences (Constantinides, 1982), recursive preferences allowing for a partial separation between the coefficient of relative risk aversion and the coefficient of intertemporal substitution (Epstein and Zin, 1989, 1991) and various forms of agent heterogeneity (following the work of Constanti nides, 1982; Mankiw, 1986; Heaton and Lucas, 1992; Telmer, 1993).