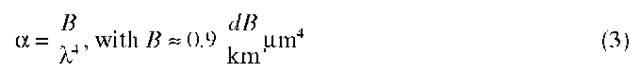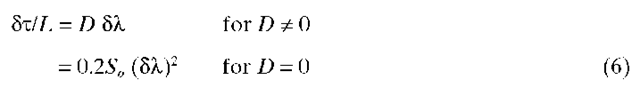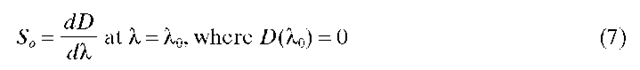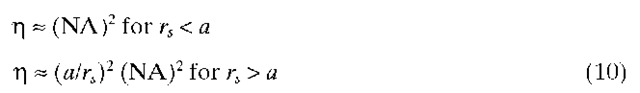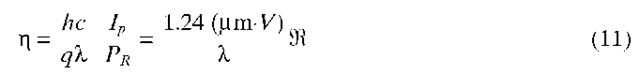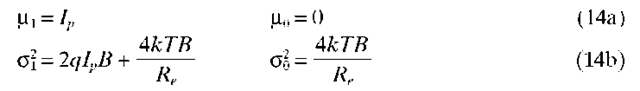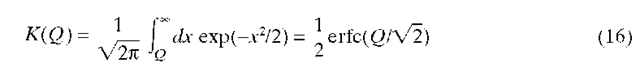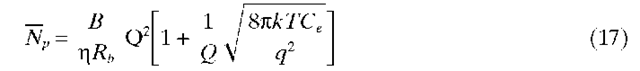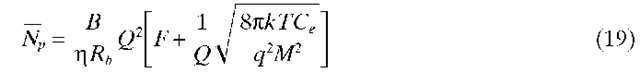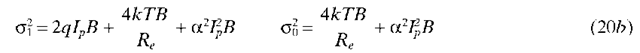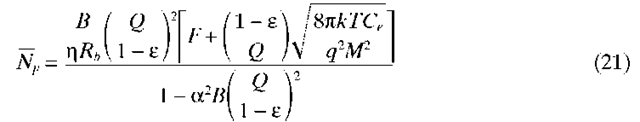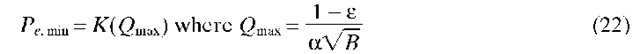INTRODUCTION
Basic elements of an optical fiber communication system include the transmitter [laser or light-emitting diode (LED)], fiber (multimode, single-mode, or dispersion-shifted), and the receiver [positive-intrinsic-negative (PIN) diode and avalanche photodetector (APD) detectors, coherent detectors, optical preamplifiers, receiver electronics]. Receiver sensitivities of digital systems are compared on the basis of the number of photons per bit required to achieve a given bit error probability, and eye degradation and error floor phenomena are described. Laser relative intensity noise and nonlinearities are shown to limit the performance of analog systems. Networking applications of optical amplifiers and wavelength-division multiplexing are considered, and future directions are discussed.
Although the light-guiding property of optical fibers has been known and used for many years, it is only relatively recently that optical fiber communications has become both a possibility and a reality.1 Following the first prediction in 19662 that fibers might have sufficiently low attenuation for telecommunications, the first low-loss fiber (20 dB/km) was achieved in 1970.3 The first semiconductor laser diode to radiate continuously at room temperature was also achieved in 1970.4 The 1970s were a period of intense technology and system development, with the first systems coming into service at the end of the decade. The 1980s saw both the growth of applications (service on the first transatlantic cable in 1988) and continued advances in technology. This evolution continued in the 1990s with the advent of optical amplifiers and with the applications emphasis turning from point-to-point links to optical networks.
This topic provides an overview of the basic technology, systems, and applications of optical fiber communication. It is an update and compression of material presented at a 1994 North Atlantic Treaty Organization (NATO) Summer School.5
BASIC TECHNOLOGY
This section considers the basic technology components of an optical fiber communications link, namely the fiber, the transmitter, and the receiver, and discusses the principal parameters that determine communications performance.
Fiber
An optical fiber is a thin filament of glass with a central core having a slightly higher index of refraction than the surrounding cladding. From a physical optics standpoint, light is guided by total internal reflection at the core-cladding boundary. More precisely, the fiber is a dielectric waveguide in which there are a discrete number of propagating modes.6 If the core diameter and the index difference are sufficiently small, only a single mode will propagate. The condition for single-mode propagation is that the normalized frequency V be less than 2.405, where
and a is the core radius, X is the free space wavelength, and n1 and n2 are the indexes of refraction of the core and cladding, respectively. Multimode fibers typically have a fractional index difference (A) between core and cladding of between 1 and 1.5 percent and a core diameter of between 50 and 100 |im. Single-mode fibers typically have A = 0.3% and a core diameter of between 8 and 10 |im.
The fiber numerical aperture (NA), which is the sine of the half-angle of the cone of acceptance, is given by
Single-mode fibers typically have an NA of about 0.1, whereas the NA of multimode fibers is in the range of 0.2 to 0.3.
From a transmission system standpoint, the two most important fiber parameters are attenuation and bandwidth.
Attenuation. There are three principal attenuation mechanisms in fiber: absorption, scattering, and radiative loss. Silicon dioxide has resonance absorption peaks in the ultraviolet (electronic transitions) and in the infrared beyond 1.6 |im (atomic vibrational transitions), but is highly transparent in the visible and near-infrared.
Radiative losses are generally kept small by using a sufficiently thick cladding (communication fibers have an outer diameter of 125 |im), a compressible coating to buffer the fiber from external forces, and a cable structure that prevents sharp bends.
In the absence of impurities and radiation losses, the fundamental attenuation mechanism is Rayleigh scattering from the irregular glass structure, which results in index of refraction fluctuations over distances that are small compared to the wavelength. This leads to a scattering loss
for "best" fibers. Attenuation as a function of wavelength is shown in Fig. 1. The attenuation peak at X = 1.4 |im is a resonance absorption due to small amounts of water in the fiber, although fibers now may be made in which this peak is absent. Initial systems operated at a wavelength around 0.85 |im owing to the availability of sources and detectors at this wave- length.
FIGURE 1 Fiber attenuation as a function of wavelength. Dashed curve shows Rayleigh scattering. Solid curve indicates total attenuation including resonance absorption at 1.38 |im from water and tail of infrared atomic resonances above 1.6 |im.
Present systems (other than some short-distance data links) generally operate at wavelengths of 1.3 or 1.55 |m. The former, in addition to being low in attenuation (about 0.32 dB/km for best fibers), is the wavelength of minimum intramodal dispersion (see the next section) for standard single-mode fiber. Operation at 1.55 |m allows even lower attenuation (minimum is about 0.16 dB/km) and the use of erbium-doped-fiber amplifiers (see Sec. 2.5), which operate at this wavelength.
Dispersion. Pulse spreading (dispersion) limits the maximum modulation bandwidth (or maximum pulse rate) that may be used with fibers. There are two principal forms of dispersion: intermodal dispersion and intramodal dispersion. In multimode fiber, the different modes experience different propagation delays resulting in pulse spreading. For graded-index fiber, the lowest dispersion per unit length is given approximately by7
[Grading of the index of refraction of the core in a nearly parabolic function results in an approximate equalization of the propagation delays. For a step-index fiber, the dispersion per unit length is 8x/L = n1A/c, which for A=0.01 is 1000 times larger than that given by Eq. (4).]
Bandwidth is inversely proportional to dispersion, with the proportionality constant dependent on pulse shape and how bandwidth is defined. If the dispersed pulse is approximated by a Gaussian pulse with 8t being the full width at the half-power point, then the -3-dB bandwidth B is given by
Multimode fibers are generally specified by their bandwidth in a 1-km length. Typical specifications are in the range from 200 MHz to 1 GHz. Fiber bandwidth is a sensitive function of the index profile and is wavelength dependent, and the scaling with length depends on whether there is mode mixing.8 Also, for short-distance links, the bandwidth is dependent on the launch conditions. Multimode fibers are generally used only when the bit rates and distances are sufficiently small that accurate characterization of dispersion is not of concern, although this may be changing with the advent of graded-index plastic optical fiber for high-bit-rate short-distance data links.
Although there is no intermodal dispersion in single-mode fibers,* there is still dispersion within the single mode (intramodal dispersion) resulting from the finite spectral width of the source and the dependence of group velocity on wavelength. The intramodal dispersion per unit length is given by
where D is the dispersion coefficient of the fiber, 8X is the spectral width of the source, and So is the dispersion slope
If both intermodal and intramodal dispersion are present, the square of the total dispersion is the sum of the squares of the intermodal and intramodal dispersions. For typical digital systems, the total dispersion should be less than half the interpulse period T. From Eq. (5) this corresponds to an effective fiber bandwidth that is at least 0.88/T
There are two sources of intramodal dispersion: material dispersion, which is a consequence of the index of refraction being a function of wavelength, and waveguide dispersion, which is a consequence of the propagation constant of the fiber waveguide being a function of wavelength.
For a material with index of refraction n(X), the material dispersion coefficient is given by
For silica-based glasses, Dmat has the general characteristics shown in Fig. 2. It is about -100 ps/kmnm at a wavelength of 820 nm, goes through zero at a wavelength near 1300 nm, and is about 20 ps/kmnm at 1550 nm.
For step-index single-mode fibers, waveguide dispersion is given approximately by10
For conventional single-mode fiber, waveguide dispersion is small (about -5 ps/kmnm at 1300 nm). The resultant D(X) is then slightly shifted (relative to the material dispersion curve) to longer wavelengths, but the zero-dispersion wavelength (Xo) remains in the vicinity of 1300 nm. However, if the waveguide dispersion is made larger negative by decreasing a or equiva-lently by tapering the index of refraction in the core the zero-dispersion wavelength may be shifted to the vicinity of 1550 nm (see Fig. 2). Such fibers are called dispersion-shifted fibers and are advantageous because of the lower fiber attenuation at this wavelength and the advent of erbium-doped-fiber amplifiers (see Sec. 8.5). Note that dispersion-shifted fibers have a smaller slope at the dispersion minimum (So = 0.06 ps/km nm2 compared to So = 0.09 ps/km nm2 for conventional single-mode fiber).
FIGURE 2 Intramodal dispersion coefficient as a function of wavelength. Dotted curve shows -Dmat; dashed curve shows Dwg to achieve D (solid curve) with dispersion 0 at 1.55 |im.
With more complicated index of refraction profiles, it is possible, at least theoretically, to control the shape of the waveguide dispersion such that the total dispersion is small in both the 1300- and 1550-nm bands, leading to dispersion-flattened fibers.11
Transmitting Sources
Semiconductor light-emitting diodes (LEDs) or lasers are the primary light sources used in fiber-optic transmission systems. The principal parameters of concern are the power coupled into the fiber, the modulation bandwidth, and (because of intramodal dispersion) the spectral width.
Light-Emitting Diodes (LEDs). LEDs are forward-biased positive-negative (PN) junctions in which carrier recombination results in spontaneous emission at a wavelength corresponding to the energy gap. Although several milliwatts may be radiated from high-radiance LEDs, the radiation is over a wide angular range, and consequently there is a large coupling loss from an LED to a fiber. Coupling efficiency (n = ratio of power coupled to power radiated) from an LED to a fiber is given approximately by12
where rs is the radius of the LED. Use of large-diameter, high-NA multimode fiber improves the coupling from LEDs to fiber. Typical coupling losses are 10 to 20 dB for multimode fibers and more than 30 dB for single-mode fibers.
In addition to radiating over a large angle, LED radiation has a large spectral width (about 50 nm at X = 850 nm and 100 nm at X = 1300 nm) determined by thermal effects. Systems employing LEDs at 850 nm tend to be intramodal-dispersion-limited, whereas those at 1300 nm are intermodal-dispersion-limited.
Owing to the relatively long time constant for spontaneous emission (typically several nanoseconds), the modulation bandwidths of LEDs are generally limited to several hundred MHz. Thus, LEDs are generally limited to relatively short-distance, low-bit-rate applications.
Lasers. In a laser, population inversion between the ground and excited states results in stimulated emission. In edge-emitting semiconductor lasers, this radiation is guided within the active region of the laser and is reflected at the end faces.* The combination of feedback and gain results in oscillation when the gain exceeds a threshold value. The spectral range over which the gain exceeds threshold (typically a few nanometers) is much narrower than the spectral width of an LED. Discrete wavelengths within this range, for which the optical length of the laser is an integer number of half-wavelengths, are radiated. Such a laser is termed a multilongitudinal mode Fabry-Perot laser. Radiation is confined to a much narrower angular range than for an LED, and consequently may be efficiently coupled into a small-NA fiber. Coupled power is typically about 1 mW.
The modulation bandwidth of lasers is determined by a resonance frequency caused by the interaction of the photon and electron concentrations.14 Although this resonance frequency was less than 1 GHz in early semiconductor lasers, improvements in materials have led to semiconductor lasers with resonance frequencies (and consequently modulation bandwidths) in excess of 10 GHz. This not only is important for very high-speed digital systems, but now also allows semiconductor lasers to be directly modulated with microwave signals. Such applications are considered in Sec. 2.7.
Although multilongitudinal-mode Fabry-Perot lasers have a narrower spectral spread than LEDs, this spread still limits the high-speed and long-distance capability of such lasers. For such applications, single-longitudinal-mode (SLM) lasers are used. SLM lasers may be achieved by having a sufficiently short laser (less than 50 |im), by using coupled cavities (either external mirrors or cleaved coupled cavities15), or by incorporating a diffraction grating within the laser structure to select a specific wavelength. The latter has proven to be most practical for commercial application, and includes the distributed feedback (DFB) laser, in which the grating is within the laser active region, and the distributed Bragg reflector (DBR) laser, where the grating is external to the active region.16
There is still a finite line width for SLM lasers. For lasers without special stabilization, the line width is on the order of 0.1 nm. Expressed in terms of frequency, this corresponds to a frequency width of 12.5 GHz at a wavelength of 1550 nm. (Wavelength and frequency spread are related by 8f/f = -8X/X, from which it follows that 8f = -c8X/X2.) Thus, unlike electrical communication systems, optical systems generally use sources with spectral widths that are large compared to the modulation bandwidth.
The finite line width (phase noise) of a laser is due to fluctuations of the phase of the optical field resulting from spontaneous emission. In addition to the phase noise contributed directly by the spontaneous emission, the interaction between the photon and electron concentrations in semiconductor lasers leads to a conversion of amplitude fluctuations to phase fluctuations, which increases the line width.17 If the intensity of a laser is changed, this same phenomenon gives rise to a change in the frequency of the laser (chirp). Uncontrolled, this causes a substantial increase in line width when the laser is modulated, which may cause difficulties in some system applications, possibly necessitating external modulation. However, the phenomenon can also be used to advantage. For appropriate lasers under small signal modulation, a change in frequency proportional to the input signal can be used to frequency-modulate and/or to tune the laser. Tunable lasers are of particular importance in networking applications employing wavelength-division multiplexing (WDM).
Photodetectors
Fiber-optic systems generally use PIN or APD photodetectors. In a reverse-biased PIN diode, absorption of light in the intrinsic region generates carriers that are swept out by the reverse-bias field. This results in a photocurrent (Ip) that is proportional to the incident optical power (PR), where the proportionality constant is the responsivity of the photodetector; that is, ^ = IP/PR. Since the number of photons per second incident on the detector is power divided by the photon energy, and the number of electrons per second flowing in the external circuit is the photocurrent divided by the charge of the electron, it follows that the quantum efficiency (n = electrons/photons) is related to the responsivity by
For wavelengths shorter than 900 nm, silicon is an excellent photodetector, with quantum efficiencies of about 90 percent. For longer wavelengths, InGaAs is generally used, with quantum efficiencies typically around 70 percent. Very high bandwidths may be achieved with PIN photodetectors. Consequently, the photodetector does not generally limit the overall system bandwidth.
In an avalanche photodetector (APD), a larger reverse voltage accelerates carriers, causing additional carriers by impact ionization resulting in a current IAPD = MIp, where M is the current gain of the APD. As noted in Sec. 2.3, this can result in an improvement in receiver sensitivity.
RECEIVER SENSITIVITY
The receiver in a direct-detection fiber-optic communication system consists of a photodetec-tor followed by electrical amplification and signal-processing circuits intended to recover the communications signal. Receiver sensitivity is defined as the average received optical power needed to achieve a given communication rate and performance. For analog communications, the communication rate is measured by the bandwidth of the electrical signal to be transmitted (B), and performance is given by the signal-to-noise ratio (SNR) of the recovered signal. For digital systems, the communication rate is measured by the bit rate (Rb) and performance is measured by the bit error probability (Pe).
For a constant optical power transmitted, there are fluctuations of the received photocur-rent about the average given by Eq. (11). The principal sources of these fluctuations are signal shot noise (quantum noise resulting from random arrival times of photons at the detector), receiver thermal noise, APD excess noise, and relative intensity noise (RIN) associated with fluctuations in intensity of the source and/or multiple reflections in the fiber medium.
Digital On-Off-Keying Receiver
It is instructive to define a normalized sensitivity as the average number of photons per bit (Np) to achieve a given error probability, which we take here to be Pe = 10-9. Given Np, the received power when a 1 is transmitted is obtained from
where the factor of 2 in Eq. (12) is because PR is the peak power, and Np is the average number of photons per bit.
Ideal Receiver. In an ideal receiver individual photons may be counted, and the only source of noise is the fluctuation of the number of photons counted when a 1 is transmitted. This is a Poisson random variable with mean 2Np. No photons are received when a 0 is transmitted. Consequently, an error is made only when a 1 is transmitted and no photons are received. This leads to the following expression for the error probability
This is termed the quantum limit.
This is termed the quantum limit.
PIN Receiver. In a PIN receiver, the photodetector output is amplified, filtered, and sampled, and the sample is compared with a threshold to decide whether a 1 or 0 was transmitted. Let I be the sampled current at the input to the decision circuit scaled back to the corresponding value at the output of the photodetector. (It is convenient to refer all signal and noise levels to their equivalent values at the output of the photodetector.) I is then a random variable with means and variances given by
where the subscripts 1 and 0 refer to the bit transmitted, kT is the thermal noise energy, and Re is the effective input noise resistance of the amplifier. Note that the noise values in the 1 and 0 states are different owing to the shot noise in the 1 state.
Calculation of error probability requires knowledge of the distribution of I under the two hypotheses. Under the assumption that these distributions may be approximated by gaussian distributions with means and variances given by Eq. (14), the error probability may be shown to be given by (Chap. 4 in Ref. 18)
where
It can be shown from Eqs. (11), (12), (14), and (15) that
where
is the effective noise capacitance of the receiver, and from Eq. (16), Q = 6 for Pe = 10-9. The minimum bandwidth of the receiver is half the bit rate, but in practice B/Rb is generally about 0.7.
The gaussian approximation is expected to be good when the thermal noise is large compared to the shot noise. It is interesting, however, to note that Eq. (17) gives Np = 18 when Ce = 0, B/Rb = 0.5, n = 1, and Q = 6. Thus, even in the shot noise limit, the gaussian approximation gives a surprisingly close result to the value calculated from the correct Poisson distribution. It must be pointed out, however, that the location of the threshold calculated by the gaussian approximation is far from correct in this case. In general, the gaussian approximation is much better in estimating receiver sensitivity than in establishing where to set receiver thresholds.
Low-input-impedance amplifiers are generally required to achieve the high bandwidths required for high-bit-rate systems. However, a low input impedance results in high thermal noise and poor sensitivity. High-input-impedance amplifiers may be used, but this narrows the bandwidth, which must be compensated for by equalization following the first-stage amplifier. Although this may result in a highly sensitive receiver, the receiver will have a poor dynamic range owing to the high gains required in the equalizer.19 Receivers for digital systems are generally implemented with transimpedance amplifiers having a large feedback resistance. This reduces the effective input noise capacitance to below the capacitance of the photodiode, and practical receivers can be built with C ~ 0.1 pF. Using this value of capacitance and B/Rb = 0.7, n = 0.7, and Q = 6, Eq. (17) gives Np = 2600. Note that this is about 34 dB greater than the value given by the quantum limit.
APD Receiver. In an APD receiver, there is additional shot noise owing to the excess noise factor F of the avalanche gain process. However, thermal noise is reduced because of the current multiplication gain M before thermal noise is introduced. This results in a receiver sensitivity given approximately by*
The excess noise factor is an increasing function of M, which results in an optimum M to minimize Np.19 Good APD receivers at 1300 and 1550 nm typically have sensitivities of the order of 1000 photons per bit. Owing to the lower excess noise of silicon APDs, sensitivity of about 500 photons per bit can be achieved at 850 nm.
Impairments. There are several sources of impairment that may degrade the sensitivity of receivers from the values given by Eqs. (17) and (19). These may be grouped into two general classes: eye degradations and signal-dependent noise.
An eye diagram is the superposition of all possible received sequences. At the sampling point, there is a spread of the values of a received 1 and a received 0. The difference between the minimum value of a received 1 and the maximum value of the received 0 is known as the eye opening. This is given by (1 – e)Ip where £ is the eye degradation. The two major sources of eye degradation are intersymbol interference and finite laser extinction ratio. Intersymbol interference results from dispersion, deviations from ideal shaping of the receiver filter, and low-frequency cutoff effects that result in direct current (DC) offsets.
Signal-dependent noises are phenomena that give a variance of the received photocurrent that is proportional to I2p and consequently lead to a maximum signal-to-noise ratio at the output of the receiver. Principal sources of signal-dependent noise are laser relative intensity noise (RIN), reflection-induced noise, mode partition noise, and modal noise. RIN is a consequence of inherent fluctuations in laser intensity resulting from spontaneous emission (Ref. 17; Chap. 4 in Ref. 18). This is generally sufficiently small that it is not of concern in digital systems, but is an important limitation in analog systems requiring high signal-to-noise ratios (see Sec. 2.7). Reflection-induced noise is the conversion of laser phase noise to intensity noise by multiple reflections from discontinuities (such as at imperfect connectors.) This may result in a substantial RIN enhancement that can seriously affect digital as well as analog sys-tems.20 Mode partition noise occurs when Fabry-Perot lasers are used with dispersive fiber.
Fiber dispersion results in changing phase relation between the various laser modes, which results in intensity fluctuations. The effect of mode partition noise is more serious than that of dispersion alone.21 Modal noise is a similar phenomenon that occurs in multimode fiber when relatively few modes are excited and these interfere.
Eye degradations are accounted for by replacing Eq. (14a) by
and signal-dependent noise by replacing Eq. (14b) by
and a2 is the relative spectral density of the signal-dependent noise. (It is assumed that the signal-dependent noise has a large bandwidth compared to the signal bandwidth B.) With these modifications, the sensitivity of an APD receiver becomes
where the PIN expression is obtained by setting F = 1 and M = 1. It follows from Eq. (21) that there is a minimum error probability (error floor) given by
The existence of eye degradations and signal-dependent noise causes an increase in the receiver power (called power penalty ) required to achieve a given error probability.