Nonlinear Effects in Optical Fibers Part 2

STIMULATED BRILLOUIN SCATTERING

The stimulated Brillouin scattering process (SBS) involves the input of a single intense optical wave at frequency m2, which initiates a copropagating acoustic wave at frequency op. The acoustic wave is manifested as a traveling index grating in the fiber, which back-diffracts a portion of the original input. The backward (Stokes) wave is Doppler-shifted to a lower frequency rn1 and is proportional to the phase conjugate of the input.29 The backward wave is amplified as it propagates, with the gain increasing with increasing input (pump) power.

The beam interaction geometry is shown in Fig. 3. Usually, the Stokes wave builds up spontaneously, but can be inputted at the far end. The effect can be understood by considering a case in which counter-propagating Stokes and pump waves exist that together form a moving interference pattern whose velocity is proportional to the difference frequency m2 – m1. Coupling between the waves will occur via SBS when the interference pattern velocity is in the vicinity of the acoustic wave velocity vp. It is the interference pattern that forms and reinforces the acoustic wave through electrostriction. With a single input, spontaneous scattering from numerous shock waves occurs, with preferential feedback from the acoustic wave that matches the condition just described. With the Stokes wave generated (although it is initially weak), the acoustic wave is reinforced, and so backscattering increases.

FIGURE 3 Beam geometry for stimulated Brillouin scattering in an optical fiber.

In terms of the wave vector magnitudes, the condition for phase matching is given by kp = k1 + k2. Since the sound frequency is much less than those of the two optical waves, we can write kp ~ 2k2. Then, since kp = fp/vp, it follows that f ~ 2nf2vp/c, where n is the refractive index (assumed to be the same value at both optical frequencies). The Brillouin frequency shift under phase-matched conditions thus becomes

This yields a value of about 11 GHz, with vp ~ 6 km/s in fused silica and X2 = 1.55 |im.

The process can be described by the nonlinear polarization produced by the product of complex fields, E1, E*, and E2; this yields a polarization at m1 that propagates with wave vector k1 in the direction of the Stokes wave. Another polarization, describing back-coupling from Stokes to pump, involves the product E1E*1E2. Substituting fields and polarizations into the wave equation yields the following coupled equations that describe the evolution of the optical intensities with distance (pp. 214-220 of Ref. 18):

where a is the linear loss coefficient. The Brillouin gain is given by

where m10 is the Stokes frequency at precise phase matching, ap is the loss coefficient for the acoustic wave, and the peak gain gb0 is a function of the material parameters. The Brillouin line width, defined as the full width at half-maximum of gb, is Amb = vpap. In optical fibers, Af = Acob/2rc is typically between 10 and 30 MHz (p. 374 of Ref. 16) and gb0 = 4.5 x 10-9 cm/W.20 Signal bandwidths in high-data-rate communication systems greatly exceed the Brillouin line width, and so SBS is typically too weak to be considered a source of noise or signal depletion. This is to be compared to stimulated Raman scattering, which supports considerable gain over approximately 5 THz. Consequently, SRS is a much more serious problem in high-data-rate systems.

Using analysis methods similar to those employed in SRS, a critical condition (or threshold) can be defined for SBS, at which the backscattered power is equal to the input power:30

where kB is Boltzmann’s constant and T is the temperature in degrees Kelvin. The gain parameter is:

with Leff as defined in Eq. (17). Equation (22) is approximately satisfied when Gb ~ 21.30 In practice, the backscattered power will always be less than the input power, since pump depletion will occur. Nevertheless, this condition is used as a benchmark to determine the point at which SBS becomes excessive in a given system.31 In one study, it was found that Gb ~ 21 yields the pump power required to produce an SBS output that is at the level of Rayleigh back-scattering.32 Pump powers required to achieve threshold can be on the order of a few milliwatts for CW or narrowband signals, but these increase substantially for broadband signals.33 Reduction of SBS is accomplished in practice by lowering the input signal power (I20) or by taking advantage of the reduction in gb that occurs when signal bandwidths (Am) exceed the Brillouin line width. Specifically, if

FOUR-WAVE MIXING

The term four-wave mixing in fibers is generally applied to wave coupling through the electronic nonlinearity in which at least two frequencies are involved and in which frequency conversion is occurring. The fact that the electronic nonlinearity is involved distinguishes four-wave mixing interactions from stimulated scattering processes because in the latter the medium was found to play an active role through the generation or absorption of optical phonons (in SRS) or acoustic phonons (in SBS). If the nonlinearity is electronic, bound electron distributions are modified according to the instantaneous optical field configurations. For example, with light at two frequencies present, electron positions can be modulated at the difference frequency, thus modulating the refractive index. Additional light will encounter the modulated index and can be up- or downshifted in frequency. In such cases, the medium plays a passive role in the interaction, as it does not absorb applied energy or release energy previously stored. The self- and cross-phase modulation processes also involve the electronic nonlinearity, but in those cases, power conversion between waves is not occurring—only phase modulation.

As an illustration of the process, consider the interaction of two strong waves at frequencies m1 and m2, which mix to produce a downshifted (Stokes) wave at m3 and an upshifted (anti-Stokes) wave at m4. The frequencies have equal spacing, that is,(Fig. 4).

 

FIGURE 4 Frequency diagram for four-wave mixing, showing pump frequenciesand sideband frequencies

All fields assume the real form:

The nonlinear polarization will be proportional toWith all

fields copolarized, complex nonlinear polarizations at m3 and rn4 appear that have the form:

whereis proportional to the nonlinear refractive index n2.

The significance of these polarizations lies not only in the fact that waves at the sideband frequencies m3 and rn4 can be generated, but that preexisting waves at those frequencies can experience gain in the presence of the two pump fields at m1 and m2. The sideband waves will contain the amplitude and phase information on the pumps, thus making this process an important crosstalk mechanism in multiwavelength communication systems. Under phase-matched conditions, the gain associated with FWM is more than twice the peak gain in SRS.34 The wave equation, when solved in steady state, yields the output intensity at either one of the sideband frequencies.35 For a medium of length L, having loss coefficient a, the sideband intensities are related to the pump intensities through

where Lef is defined in Eq. (17), and where

Other FWM interactions can occur, involving products of intensities at three different frequencies rather than two as demonstrated here. In such cases, the output wave intensities are increased by a factor of 4 over those indicated in Eqs. (28) and (29).

One method of suppressing four-wave mixing in WDM systems includes the use of unequal channel spacing.36 This assures, for example, that m3 ^ 2m1 + m2, where m1, m2, and m3 are assigned channel frequencies. Other methods involve phase-mismatching the process in some way. This is accomplished by increasing AP, which has the effect of decreasing n in Eqs. (28) and (29). Note that in the low-loss limit, where a ^ 0, Eq. (30) reduces to n = (sin2 (APL/2))/(APL/2)2. The AP expressions associated with wave generation at m3 and rn4 are given by

and

It is possible to express Eqs. (31) and (32) in terms of known fiber parameters by using a Taylor series for the propagation constant, where the expansion is about frequency om as indicated in Fig. 4, where om = (m2 + m1)/2.

In Eq. (33),are, respectively, the first, second, and third derivatives of with respect to m, evaluated at mm. These in turn relate to the fiber dispersion parameter D (ps/nmkm) and its first derivative with respect to wavelength through andUsing these relations along with Eq. (33) in Eqs. (31) and (32) results in:

where the plus sign is used forthe minus sign is used for

Phase matching is not completely described by Eq. (34), since cross-phase modulation plays a subtle role, as discussed on pp. 410-411 of Ref. 16. Nevertheless, Eq. (34) does show that the retention of moderate values of dispersion D is a way to reduce FWM interactions that would occur, for example, in WDM systems. As such, modern commercial fiber intended for use in WDM applications will have values of D that are typically in the vicinity of 2 ps/nm km.37 With WDM operation in conventional dispersion-shifted fiber (with the dispersion zero near 1.55 |im), having a single channel at the zero dispersion wavelength can result in significant four-wave mixing.38 Methods that were found to reduce four-wave mixing in such cases include the use of cross-polarized signals in dispersion-managed links39 and operation within a longer-wavelength band near 1.6 |im40 at which dispersion is appreciable and where gain-shifted fiber amplifiers are used.41

Examples of other cases involving four-wave mixing include single-wavelength systems, in which the effect has been successfully used in a demultiplexing technique for TDM signals.42 In another case, coupling through FWM can occur between a signal and broadband amplified spontaneous emission (ASE) in links containing erbium-doped fiber amplifiers.43 As a result, the signal becomes spectrally broadened and exhibits phase noise from the ASE. The phase noise becomes manifested as amplitude noise under the action of dispersion, producing a form of modulation instability.

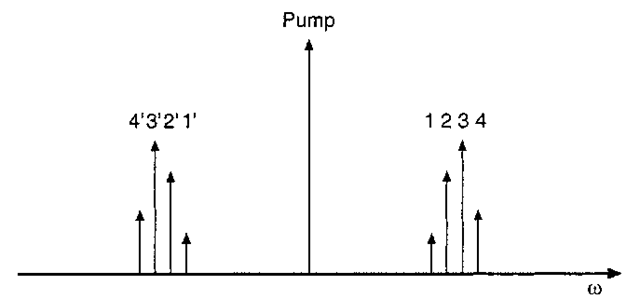
An interesting application of four-wave mixing is spectral inversion. Consider a case that involves the input of a strong single-frequency pump wave along with a relatively weak wave having a spectrum of finite width positioned on one side of the pump frequency. Four-wave mixing leads to the generation of a wave whose spectrum is the "mirror image" of that of the weak wave, in which the mirroring occurs about the pump frequency. Figure 5 depicts a representation of this, where four frequency components comprising a spectrum are shown along with their imaged counterparts.

FIGURE 5 Frequency diagram for spectral inversion using four-wave mixing with a single pump frequency.

An important application of this is pulses that have experienced broadening with chirping after propagating through a length of fiber exhibiting linear group dispersion.44 Inverting the spectrum of such a pulse using four-wave mixing has the effect of reversing the direction of the chirp (although the pulse center wavelength is displaced to a different value). When the spectrally inverted pulse is propagated through an additional length of fiber having the same dispersive characteristics, the pulse will compress to nearly its original input width. Compensation for nonlinear distortion has also been demonstrated using this method.45

CONCLUSION

An overview of fiber nonlinear effects has been presented here in which emphasis is placed on the basic concepts, principles, and perspectives on communication systems. Space is not available to cover the more subtle details of each effect or the interrelations between effects that often occur. The text by Agrawal16 is recommended for further in-depth study, which should be supplemented by the current literature. Nonlinear optics in fibers and in fiber communication systems comprises an area whose principles and implications are still not fully understood. It thus remains an important area of current research.