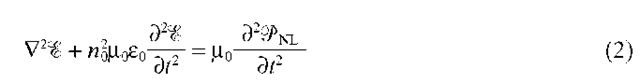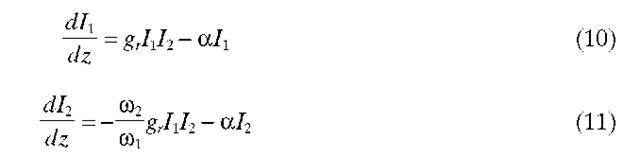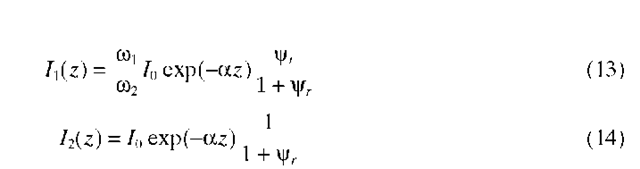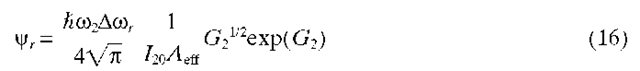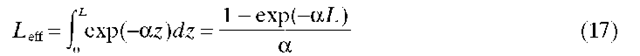Fiber nonlinearities are important in optical communications, both as useful attributes and as characteristics to be avoided. They must be considered when designing long-range high-data-rate systems that involve high optical power levels and in which signals at multiple wavelengths are transmitted. The consequences of nonlinear transmission can include (1) the generation of additional signal bandwidth within a given channel, (2) modifications of the phase and shape of pulses, (3) the generation of light at other wavelengths at the expense of power in the original signal, and (4) crosstalk between signals at different wavelengths and polarizations. The first two, arising from self-phase modulation, can be used to advantage in the generation of solitons—pulses whose nonlinear phase modulation compensates for linear group dispersion in the fiber channel1 or in fiber gratings,2 leading to pulses that propagate without changing shape or width (see Chap. 7). The third and fourth effects arise from stimulated Raman or Brillouin scattering or four-wave mixing. These can be used to advantage when it is desired to generate or amplify additional wavelengths, but they must usually be avoided in systems.
KEY ISSUES IN NONLINEAR OPTICS IN FIBERS
Optical fiber waveguides, being of glass compositions, do not possess large nonlinear coefficients. Nonlinear processes can nevertheless occur with high efficiencies since intensities are high and propagation distances are long. Even though power levels are usually modest (a few tens of milliwatts), intensities within the fiber are high due to the small cross-sectional areas involved. This is particularly true in single-mode fiber, where the LP01 mode typically presents an effective cross-sectional area of between 10-7 and 10-8 cm2, thus leading to intensities on the order of MW/cm2. Despite this, long interaction distances are usually necessary to achieve nonlinear mixing of any significance, so processes must be phase matched, or nearly so. Strategies to avoid unwanted nonlinear effects usually involve placing upper limits on optical power levels, and if possible, choosing other parameters such that phase mismatching occurs. Such choices may include wavelengths or wavelength spacing in wavelength-division multiplexed systems, or may be involved in special fiber waveguide designs.3
The generation of light through nonlinear mixing arises through polarization of the medium, which occurs through its interaction with intense light. The polarization consists of an array of phased dipoles in which the dipole moment is a nonlinear function of the applied field strength. In the classical picture, the dipoles, once formed, reradiate light to form the nonlinear output. The medium polarization is conveniently expressed through a power series expansion involving products of real electric fields:
in which the % terms are the linear, second-, and third-order susceptibilities. Nonlinear processes are described through the product of two or more optical fields to form the nonlinear polarization 9NL, consisting of all terms of second order and higher in Eq. (1).
The second-order term in Eq. (1) [involving %(2)] describes three-wave mixing phenomena, such as second-harmonic generation. The third-order term describes four-wave mixing (FWM) processes and stimulated scattering phenomena. In the case of optical fibers, second-order processes are generally not possible, since these effects require noncen-trosymmetric media.4 In amorphous fiber waveguides, third-order effects [involving %(3)] are usually seen exclusively, although second-harmonic generation can be observed in special instances.5
The interactions between fields and polarizations are described by the nonlinear wave equation:
where % and 9 are the sums of all electric fields and nonlinear polarizations that are present, and where n0 is the refractive index of the medium. The second-order differential equation is usually reduced to first order through the slowly varying envelope approximation (SVEA):
where E is the complex field amplitude. The interpretation of the SVEA is that the changes in field amplitude that occur over distances on the order of a wavelength are very large compared to variations in the rate of change over the same distance. The wave equation will separate according to frequencies or propagation directions, yielding sets of coupled differential equations that, under the SVEA, are first order. These describe the growth or decay of fields involved in the mixing process.
The requirement for phase matching is that the nonlinear polarization wave and the electric field associated with the generated wave propagate with the same phase constant; that is, their phase velocities are equal. Phase-matched processes in fiber include those that involve (1) interacting waves at the same wavelength and polarization, such as self-and cross-phase modulation, as well as other degenerate Kerr-type interactions; and (2) stimulated scattering processes (Raman and Brillouin), in addition to cross-phase modulation involving two wavelengths. Four-wave mixing processes involving light at different wavelengths can occur that are not precisely phase matched but that can nevertheless yield high efficiencies. Matters are further complicated by the fact that different nonlinear processes can occur simultaneously, with each affecting the performance of the other. Nonlinear effects are usually favored to occur under pulsed operation, since high peak powers can be achieved with comparatively modest average powers. Consequently, group velocity matching is desirable (although not always required) to achieve efficient mixing between pulses.
SELF- AND CROSS-PHASE MODULATION
Self-phase modulation (SPM) can occur whenever a signal having a time-varying amplitude is propagated in a nonlinear material. The origin of the effect is the refractive index of the medium, which will change with the instantaneous signal intensity. The complex nonlinear polarization for the process is:
where E0(t) is the time-varying electric field amplitude that describes the pulse or signal envelope, and where the frequency m is the same as that of the input light. Incorporating this polarization and the field into the wave equation leads to a modified refractive index over the original zero-field value n0. The net index becomes:6
where the nonlinear refractive index is given by
In fused silica it has the value
Equation (5) can also be expressed in terms of light intensity through
In optical fibers the index is modified
from the effective mode index of the single-mode fiber neff (which assumes the role of n0).
The complex field as it propagates through the medium can be expressed as:
which exhibits phase modulation that follows the shape of the intensity envelope. The instantaneous frequency is found through the time derivative of the phase:
The effects of self-phase modulation on pulse propagation can be qualitatively observed from Eqs. (6) and (7). First, additional frequency components are placed on the pulse, thus increasing its spectral width. Second, a frequency sweep (chirp) imposed on the pulse, the direction of which depends on the sign of dI/dt. The latter feature is particularly important in optical fibers, since the imposed frequency sweep from SPM will either add to or subtract from the chirp imposed by linear group dispersion. If the chirp directions for self-phase modulation and group dispersion are opposite, an effective cancellation may occur, leading to the formation of an optical soliton. In more conventional systems in which solitons are not employed, SPM must be considered as a possible benefit or detriment to performance, as some pulse shaping (which could include broadening or compression) can occur;8,9 however, such systems can in theory yield excellent performance.10 Furthermore, in systems employing fiber amplifiers, the change in refractive index associated with the signal-induced upper state population in erbium has been shown to be an important performance factor.11 An additional effect can occur when pulse spectra lie within the anomalous group dispersion regime of the fiber; pulse breakup can occur as a result of modulation instability, in which the interplay between dispersive and nonlinear contributions to pulse shaping becomes unstable.12
Cross-phase modulation (XPM) is similar to SPM, except that two overlapping but distinguishable pulses (having, for example, different frequencies or polarizations) are involved. One pulse will modulate the index of the medium, which then leads to phase modulation of an overlapping pulse. XPM thus becomes a cross-talk mechanism between two channels if phase encoding is employed or if intensity modulation is used in dispersive systems.13,14 No transfer of energy occurs between channels, however, which distinguishes the process from other crosstalk mechanisms in which growth of signal power in one channel occurs at the expense of power in another. The strength of the effect is enhanced by a factor of 2 over that which can be obtained by a single field acting on itself (the nonlinear refractive index n2 is effectively doubled in XPM).15 The XPM process, while twice as strong as SPM, is effectively weakened by the fact that pulses of differing frequencies or polarizations are generally not group velocity matched, and so cannot maintain overlap indefinitely. The efficiency is further reduced if the interaction occurs between cross-polarized waves; in this case the nonlinear tensor element (and thus the effective nonlinear index) is a factor of M less than the tensor element that describes copolarized waves (pp. 164-165 in Ref. 6).
Self- and cross-phase modulation are analyzed by way of coupled equations of the nonlinear Schrodinger form,16 which describes the evolution over time and position of the electric field envelopes of two pulses, E0a and E0b, where SVEA is used and where pulse widths are on the order of 1 ps or greater:
In these equations,
are the group delays of the pulses at the two frequencies or polarizations over a unit distance; p2;- are the group dispersion parameters associated with the two pulses; and Yj = n2ro/(cAeH), where Aef£ is the effective cross-sectional area of the fiber mode. The coefficient 8 is equal to 2 for copolarized pulses of different frequencies and is if the pulses are cross-polarized. Propagation loss characterized by coefficients a;- is assumed. The equation form that describes the propagation with SPM of a single pulse—E0a, for example—is found from Eq. (8) by setting E0b = 0. The terms on the right sides of Eqs. (8) and (9) describe in order the effects of group dispersion, SPM, XPM, and loss.
For subpicosecond pulses, the accuracy of Eqs. (8) and (9) begins to degrade as pulse band-widths increase with decreasing temporal width. Additional terms are usually incorporated in the equations as pulse widths are reduced to the vicinity of 100 fs. These embody (1) cubic dispersion, which becomes important as bandwidth increases, and (2) changes in group velocity with intensity. This latter effect can result in self-steepening, in which the pulse trailing edge shortens to the point of forming an optical shock front (pp. 113-120 of Ref. 16) under appropriate conditions. An additional consequence of broad pulse spectra is that power conversion from high-frequency components within a pulse to those at lower frequencies can occur via stimulated Raman scattering, provided the interacting components are sufficiently separated in wavelength. The effect is an overall red shift of the spectrum. At sufficiently high intensities, cross-coupling between pulses having different center wavelengths can also occur through Raman scattering, regardless of pulse width.
STIMULATED RAMAN SCATTERING
In stimulated Raman scattering (SRS), coupling occurs between copropagating light waves whose frequency difference is in the vicinity of resonances of certain molecular oscillation modes. In silica-based fibers, stretch vibrational resonances occur between Si and O atoms in several possible modes within the glass matrix (see Ref. 17 for illustrations of the important modes in pure silica). In the Stokes process, light at frequency m2 (pump wave) is downshifted to light at m1 (Stokes wave), with the excess energy being absorbed by the lattice vibrational modes (manifested in the generation of optical phonons). The process is either spontaneous, 
in which the Stokes wave builds up from noise, or is stimulated, in which both waves are present in sufficient strength to generate a beat frequency that excites the oscillators and promotes coupling. A fiber Raman amplifier works on this principle, in which an input signal at m1 experiences gain in the presence of pump light at m2. Figure 1 shows the beam geometry in which an input wave at m1 and intensity I10 can emerge at the far end with amplified value I1L. This occurs in the presence of the pump wave at m2 that has initial intensity I20 and that emerges with depleted intensity I2L.
Back-conversion from m1 to m2 (the inverse Raman effect) will also occur once the Stokes wave reaches sufficient intensity, but gain will only occur for the Stokes wave. Both processes are phase matched, and so occur with high efficiency in long fibers. The back-conversion process is to be distinguished from anti-Stokes scattering, in which pump light at m2 is upshifted to frequency m3, with the additional energy being supplied by optical phonons associated with the previously excited medium. The anti-Stokes process is rarely seen in fiber transmission because (1) it is phase mismatched and (2) it requires a substantial population of excited oscillators, which is not the case at thermal equilibrium.
Figure 2 shows the measured Raman gain for the Stokes wave in fused silica. The gain is plotted as a function of difference frequency between the interacting waves measured in cm-1 (to convert this to wavelength shift, use the formula AX = XpAf(cm-1), where Xp is the pump wavelength). Other fiber constituents such as GeO2, P2O5, and B2O3 exhibit their own Raman resonances, which occur at successively greater wavelength shifts;19 the effects of these will be weak, since their concentration in the fiber is generally small. Thus the dominant Raman shifts in optical fiber are associated with SiO2, and occur within the range of 440 to 490 cm-1, as is evident in Fig. 2.
Nonlinear polarizations at frequencies m1 and m2 can be constructed that are proportional to products of the Stokes and pump fields, Ef1 and E22. These are of the form PgL m iE22i2Ef1 (Stokes generation) and PNL m iEf1i2E22 (the inverse Raman effect). Substituting these polarizations and the two fields into the wave equation, using the SVEA, and assuming copolarized fields leads to the following coupled equations involving the Stokes and pump wave intensities I1 and I2:18
where the loss terms involving a (the fiber loss per unit distance) are added phenomenologi-cally. The Raman gain function gr is expressed in a general way as
where A is a function of the material parameters and
is a normalized line shape function, which is either derived from theory or experimentally measured (determined from Fig. 2, for example). With X2 expressed in
The solutions of Eqs. (10) and (11) are:
FIGURE 1 Beam geometry for stimulated Raman scattering in an optical fiber.
FIGURE 2 Raman gain spectrum in fused silica.
In these equations,
are the Stokes and pump intensities at the fiber input. The coupling parameter yr assumes different forms, depending upon whether the input Stokes intensity I10 is present or not. If I10 is present, and if its magnitude is much greater than light from spontaneous Raman scattering, we have:
When no Stokes input is present, the signal builds up from spontaneous Raman scattering, and the coupling parameter in this case becomes:
with the gain parameters defined through
The effective length of the fiber accounts for the reduction of Stokes and pump intensities as a result of loss, and is defined as
The effective area of a single-mode fiber Aeff is calculated through nr0, where r0 is the mode field radius. For a multimode fiber, Aeff is usually taken as the core area, assuming that the power is uniformly distributed over the core. The power in the fiber is then P1? 2 = I1, 2AeH.
Two basic issues concerning SRS are of interest in fiber communication systems. First, pump-to-Stokes coupling provides a mechanism for crosstalk from short- to long-wavelength channels. This will occur most efficiently if the channel frequency spacing is in the vicinity of that associated with the maximum Raman gain. The Raman gain peak at approximately 500 cm-1 corresponds to a frequency spacing of 15 THz, meaning that operation at 1.55 |im produces a Stokes wave of about 1.67 |im wavelength. Two-channel operation at these wavelengths would lead to a maximum allowable signal level of about 50 mW.21 In WDM systems, within the 1.53- to 1.56-^m erbium-doped fiber amplifier window, channel spacings on the order of 100 GHz are used. Raman gain is thus considerably reduced, but is still sufficient to cause appreciable crosstalk, which can lead to system penalties of between 1 and 3 dB depending on the number of channels.22 Second, and of more importance to single-wavelength systems, is the conversion to Stokes power from the original signal—a mechanism by which signal power can be depleted. A related problem is walkoff23 occurring between the signal and Stokes pulses, since these will have different group delays. Walkoff is a means for aliasing to occur in digital transmission, unless the signal is filtered at the output. If pulses are of subpicosecond widths, additional complications arise due to the increased importance of SPM and XPM.24 In any event, an upper limit must be placed on the signal power if significant conversion to Stokes power is to be avoided. In single-wavelength systems, where crosstalk is not an issue, pulse peak powers must be kept below about 500 mW to avoid significant SRS conversion.25
A useful criterion is the so-called critical condition (or Raman threshold), defined as the condition under which the output Stokes and signal powers are equal. This occurs when yr = 1, which, from Eq. (16), leads to G2 ~ 16. SRS can also be weakened by taking advantage of the gain reduction that occurs as signal (pump) wavelengths increase, as shown in Eq. (12). For example, operation at 1.55 |im yields less SRS for a given signal power than operation at 1.3 |im.
Apart from the need to reduce SRS, the effect can be used to advantage in wavelength conversion and in amplification. Fiber Raman lasers have proven to be good sources of tunable radiation and operate at multiple Stokes wavelengths.26 Specifically, a Stokes wave can serve as a pump to generate an additional (higher-order) Stokes wave at a longer wavelength.27 Fiber Raman amplifiers have been demonstrated as repeaters in 1.3-^m wavelength systems.28
