Local Representation of Facial Features (Face Image Modeling and Representation) (Face Recognition) Part 2

Face Description Using LBP

Description of Static Face Images

In the LBP approach for texture classification [64], the occurrences of the LBP codes in an image are collected into a histogram. The classification is then performed by computing simple histogram similarities. However, considering a similar approach for facial image representation results in a loss of spatial information and therefore one should codify the texture information with their locations. One way to achieve this goal is to use the LBP texture descriptors to build several local descriptions of the face and combine them into a global description. Such local descriptions have gained interest lately which is understandable given the limitations of the holistic representations. These local feature based methods seem to be more robust against variations in pose or illumination than holistic methods.

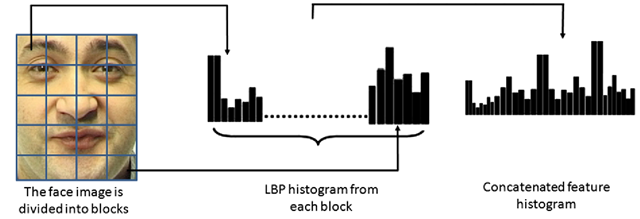
Fig. 4.6 Example of an LBP based facial representation

The basic methodology for LBP based face description is as follows: The facial image is divided into local regions and LBP texture descriptors are extracted from the each region independently. The descriptors are then concatenated to a global face description, as shown in Fig. 4.6.

The basic histogram that is used to gather information about LBP codes in an image can be extended into a spatially enhanced histogram which encodes both the appearance and the spatial relations of facial regions. As the facial regions have been determined, the spatially enhanced histogram is defined as

This histogram effectively has a description of the face on three different levels of locality: the LBP labels for the histogram contain information about the patterns on a pixel-level, the labels are summed over a small region to produce information on a regional level and the regional histograms are concatenated to build a global description of the face. It should be noted that when using the histogram based methods the regionsdo not need to be rectangular.Neither do they need to be of the same size or shape, and they do not necessarily have to cover the whole image. It is also possible to have partially overlapping regions.

This outlines the original LBP based facial representation [1, 2] that has been later adopted to various facial image analysis tasks [31, 45]. Figure 4.6 shows an example of an LBP based facial representation.

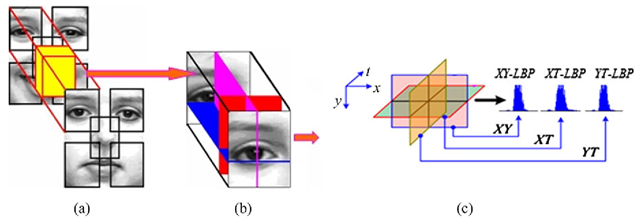
Fig. 4.7 Features in each block volume. a Block volumes; b LBP features from three orthogonal planes; c Concatenated features for one block volume with the appearance and motion

Description of Face Sequences

How can moving faces be efficiently represented? Psychophysical findings state that facial movements can provide valuable information to face analysis. Therefore, efficient facial representations should encode both appearance and motion. We thus describe an LBP based spatiotemporal representation for face analysis in videos using region-concatenated descriptors. Like in [2], an LBP description computed over a whole face sequence encodes only the occurrences of the micro-patterns without any indication about their locations. To overcome this effect, a representation in which the face image is divided into several overlapping blocks is used. The LBP-TOP histograms in each block are computed and concatenated into a single histogram, as illustrated in Fig. 4.7. All features extracted from the each volume are connected to represent the appearance and motion of the face in the sequence. The basic VLBP features could also be considered and extracted on the basis of region motion in the same way as the LBP-TOP features.

The LBP-TOP histograms in each block volume are computed and concatenated into a single histogram. All features extracted from each block volume are connected to represent the appearance and motion of the face. In this way, we effectively have a description of the face on three different levels of locality. The labels (bins) in the histogram contain information from three orthogonal planes, describing appearance and temporal information at the pixel level. The labels are summed over a small block to produce information on a regional level expressing the characteristics for the appearance and motion in specific locations, and all information from the regional level is concatenated to build a global description of the face sequence.

Face Recognition Using LBP Descriptors

This section describes the application of the LBP based face description to face recognition. Typically a nearest neighbor classification rule is used in the face recognition task. This is due to the fact that the number of training (gallery) images per subject is low, often only one. However, the idea of a spatially enhanced histogram can be exploited further when defining the distance measure for the classifier.

Fig. 4.8 a An example of a facial image divided into 7 x 7 windows. b The weights set for weighted χ 2 dissimilarity measure. The black squares indicate weight 0.0, dark gray 1.0, light gray 2.0 and white 4.0

An indigenous property of the proposed face description method is that each element in the enhanced histogram corresponds to a certain small area of the face. Based on the psychophysical findings, which indicate that some facial features (such as eyes) play a more important role in human face recognition than other features [101], it can be expected that some of the facial regions contribute more than others in terms of extra-personal variance. Utilizing this assumption the regions can be weighted based on the importance of the information they contain. Figure 4.8 shows an example of weighting different facial regions. The weighted Chi square distance can be defined as

in which x and ξ are the normalized enhanced histograms to be compared, indices i and j refer to i th bin corresponding to the j th local region and Wj is the weight for the region j.

In [1, 2,4], Ahonen et al. performed a set of experiments on the FERET face images [67]. The results showed that the LBP approach yields higher face recognition rates than the control algorithms (PCA [82], Bayesian Intra/Extra-personal Classifier (BIC) [62] and Elastic Bunch Graph Matching EBGM [89]). To gain better understanding on whether the obtained recognition results are due to general idea of computing texture features from local facial regions or due to the discriminatory power of the local binary pattern operator, we also compared LBP to three other texture descriptors, namely the gray-level difference histogram, homogeneous texture descriptor [55] and an improved version of the texton histogram [83]. The details of these experiments can be found in [4]. The results confirmed the validity of the LBP approach and showed that the performance of LBP in face description exceeds that of other texture operators as shown in Table 4.2. We believe that the main explanation for the better performance over other texture descriptors is the tolerance to monotonic gray-scale changes. Additional advantages are the computational efficiency and avoidance of gray-scale normalization prior to the LBP operator.

Table 4.2 The recognition rates obtained using different texture descriptors for local facial regions. The first four columns show the recognition rates for the FERET test sets and the last three columns contain the mean recognition rate of the permutation test with a 95% confidence interval

Method	fb	fc	dup I	dup II	lower	mean	upper
Difference histogram	0.87	0.12	0.39	0.25	0.58	0.63	0.68
Homogeneous texture	0.86	0.04	0.37	0.21	0.58	0.62	0.68
Texton Histogram	0.97	0.28	0.59	0.42	0.71	0.76	0.80
LBP (nonweighted)	0.93	0.51	0.61	0.50	0.71	0.76	0.81

Fig. 4.9 Example of Gallery and probe images from the FRGC database, and their corresponding filtered images with Tan and Triggs’ preprocessing chain [80]

Recently, Tan and Triggs developed a very effective preprocessing chain for face images and obtained excellent results using LBP-based face recognition for the FRGC database [80]. Since then, many others have adopted their preprocessing chain for applications dealing with severe illumination variations. Figure 4.9 shows an example of gallery and probe images from the FRGC database and the corresponding filtered images with the preprocessing method.

Chan et al. [12] considered multi-scale LBPs and derived new face descriptor from Linear Discriminant Analysis (LDA) of multi-scale local binary pattern histograms. The face image is first partitioned into several non-overlapping regions. In each region, multi-scale uniform LBP histograms are extracted and concatenated into a regional feature. The features are then projected on the LDA space to be used as a discriminative facial descriptor. The method was tested in face identification on the standard FERET database and in face verification on the XM2VTS database with very promising results.

Zhang et al. [95] considered the LBP methodology for face recognition and used AdaBoost learning algorithm for selecting an optimal set of local regions and their weights. This yielded to a smaller feature vector than that used in the original LBP approach [1]. However, no significant performance enhancement was obtained. Later, Huang et al. [36] proposed a variant of AdaBoost called JSBoost for selecting the optimal set of LBP features for face recognition.

In order to deal with strong illumination variations, Li et al. developed a very successful system combining near infrared (NIR) imaging with local binary pattern features and AdaBoost learning [49]. The invariance of LBP with respect to mono tonic gray level changes makes the features extracted from NIR images illumination invariant.

In [70], Rodriguez and Marcel proposed an approach based on adapted, client-specific LBP histograms for the face verification task. The method considers local histograms as probability distributions and computes a log-likelihood ratio instead of χ2 similarity. A generic face model is considered as a collection of LBP histograms. Then, a client-specific model is obtained by an adaptation technique from the generic model under a probabilistic framework. The reported experimental results show that the proposed method yields good performance on two benchmark databases (XM2VTS and BANCA). Later, Ahonen and Pietikainen [3] have further enhanced the face verification performance on the BANCA database by developing a novel method for estimating the local distributions of LBP labels. The method is based on kernel density estimation in xy-space, and it provides much better spatial accuracy than the block-based method of Rodriguez and Marcel [70].

LBP in Other Face-Related Problems

The LBP approach has also been adopted to several other face analysis tasks such as facial expression recognition [23, 74], gender recognition [78], age classification [86], face detection [30, 71, 91], iris recognition [79], head pose estimation [54] and 3D face recognition [48]. For instance, LBP is used in [35] with Active Shape Model (ASM) for localizing and representing facial key points since an accurate localization of such points of the face is crucial to many face analysis and synthesis problems. The local appearance of the key points in the facial images are modeled with an Extended version of Local Binary Patterns (ELBP). ELBP was proposed in order to encode not only the first derivation information of facial images but also the velocity of local variations. The experimental analysis showed that the combination ASM-ELBP enhances the face alignment accuracy compared to the original ASM method.

In [30], the authors devised another LBP based representation which is suitable for low-resolution images and has a short feature vector needed for fast processing. A specific aspect of this representation is the use of overlapping regions and a 4-neighborhood LBP operator (LBP4,1) to avoid statistical unreliability due to long histograms computed over small regions. Additionally, the holistic description of a face was enhanced by including the global LBP histogram computed over the whole face image. The proposed representation performed well in the face detection problem.

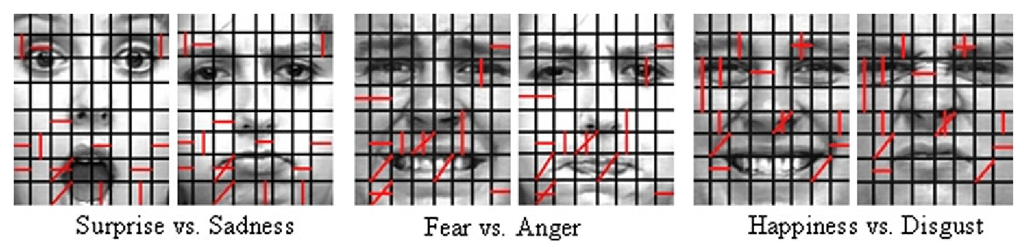
Spatiotemporal LBP descriptors, especially LBP-TOP, have been successfully utilized in many video-based applications, for example, dynamic facial expression recognition [100], visual speech recognition [102] and gender recognition from videos [29]. They can effectively describe appearance, horizontal motion and vertical motion from the video sequence. LBP-TOP based approach was also extended to include multiresolution features which are computed from different sized blocks, different neighboring samplings and different sampling scales, and utilize AdaBoost to select the slice features for all the expression classes or every class pair, to improve the performance with short feature vectors. After that, on the basis of selected slices, the location and feature types of most discriminative features for every class pair are considered. Figure 4.10 shows the selected features for two expression pairs. They are different and specific depending on the expressions.

Fig. 4.10 Selected 15 slices for different facial expression pairs

GaborFeatures

Introduction

Methods using Gabor features have been particularly successful in biometrics. For example, Daugman’s iris code [18] is The Method for iris recognition, Gabor features were used in the two best methods in the ICPR 2004 face recognition contest [57] and they are among the top performers in fingerprint matching [38], and so on. It is interesting, why feature extraction based on the Gabor’s principle of simultaneous localization in the frequency and spatial domains [25], is so successful in many applications of computer vision and image processing. The same principle was independently found as an intuitive requirement for a “general picture processing operator” by Granlund [28], and later rigorously defined in 2D by Daug-man [16].

As the well-known result in face recognition, Lades et al. developed a Gabor based system using dynamic link architecture (DLA) framework which recognizes faces by extracting a set of features (“Gabor jet”) at each node of a rectangular grid over the face image [44]. Later, Wiskott et al. extended the approach and developed the well-known Gabor wavelet-based elastic bunch graph matching (EBGM) method to label and recognize faces [89]. In the EBGM algorithm, faces are represented as graphs with nodes positioned at fiducial points (such as the eyes and the tip of the nose) and edges labeled with distance vectors. Each node contains a set of Gabor wavelet coefficients, known as a jet. Thus, the geometry of the face is encoded by the edges while the local appearance is encoded by the jets. The identification of a face consists of determining among the constructed graphs the one which maximizes the graph similarity function.

In this section, we first explain the main properties of Gabor filters, then describe how image features can be constructed from filter responses, and finally, demonstrate how these features can accurately and efficiently represent and detect facial features. Note that, similarly to LBP, Gabor filters can be used to either detect face parts or whole face for recognition. In the previous sections, we explained the use of LBP for face appearance description. For completeness, we focus below on the use of Gabor filters for representing and detecting facial landmarks.

Gabor Filter

Gabor filter is Gabor function changed into the linear filter form, that is, a signal or an image can be convolved with the filter to produce a “response image”. This process is similar to edge detection. Gabor features are formed by combining responses of several filters from a single or multiple spatial locations. Gabor function provides the minimal joint-uncertaintysimultaneously in the time (spatial) and frequency domains. In 1946, Dennis Gabor proved that: “The signal which occupies the minimum areais    the modulation product of a harmonic oscillation1′*’1 of any frequency with pulse of the form of a probability function^**’” [25]

In (4.6), a is the sharpness (time duration and bandwidth) of the Gaussian, t0 is the time shift defining the time location of the Gaussian, f0 is the frequency of the harmonic oscillations (frequency location), and φ denotes the phase shift of the oscillation. The Gabor elementary function in (4.6) has a Fourier spectrum of analytical form

Two important findings can be seen in (4.6) and (4.7): Gabor function, or more precisely its magnitude, has the Gaussian form in the time domain and frequency domain; The Gaussian is located at t0 in time and f0 in frequency; If you increase the bandwidth α, the function will shrink in time (more accurate), but stretch in frequency (more inaccurate). These are the properties which help understand Gabor filter as a linear operator operating in time and frequency simultaneously. For the linear filter form, the function is typically simplified by centering it to origin (t0 = 0) and removing the phase shift (φ = 0).

Gabor’s original idea was to synthesize signals using a set of these elementary functions. That research direction has lead to the theory of Gabor expansion (Gabor transform) [8] and more generally to the Gabor frame theory [22]. Feature extraction, however, is signal analysis. The development of the 2D Gabor elementary functions began from Granlund in 1978, when he defined some fundamental properties and proposed the form of a general picture processing operator. The general picture processing operator had a form of the Gabor elementary function in two dimensions and it was derived directly from the needs of the image processing without a connection to Gabor’s work [28]. It is noteworthy that Granlund addressed many properties, such as the octave spacing of the frequencies, that were reinvented later for the Gabor filters. Despite the original contribution of Granlund the most referred works are those conducted by Daugman [16, 17]. Daugman was the first who exclusively derived the uncertainty principle in two dimensions and showed the similarity between a structure based on the 2D Gabor functions and the organization and the characteristics of the mammalian visual system. Again, several simplifications are justifiable [39] and 2D Gabor function can be defined as

where the new parameters are β for sharpness of the second Gaussian axis and θ for its orientation. In practice, the sharpness is connected to the frequency in order to make filters self-similar (Gabor wavelets) [39]. This is achieved by setting

and by normalizing the filter. Finally, the 2D Gabor filter in the spatial domain is

where f is the central frequency of the filter, θ the rotation angle of the Gaussian major axis and the plane wave, γ the sharpness along the major axis, and η the sharpness along the minor axis (perpendicular to the wave). In the given form, the aspect ratio of the Gaussian is η/γ. The normalized 2D Gabor filter function has an analytical form in the frequency domain

The effects of the Gabor filter parameters, interpretable via the Fourier similarity theorem, are demonstrated in Fig. 4.11.

Fig. 4.11 2D Gabor filter functions with different values of the parameters /, θ, γ, and η in the space (top) and frequency domains (bottom). Left: (/ = 0.5, θ = 0ο,γ = 1.0, η = 1.0); middle-left: (/ = 1.0, Θ = 0°, γ = 1.0, η = 1.0); middle-right: (/ = 1.0, θ=0ο,γ= 2.0, η = 0.5); right: (/ = 1.0, θ = 45°, γ = 2.0, η =0.5)