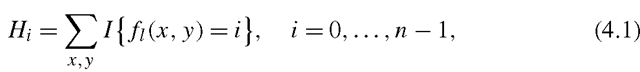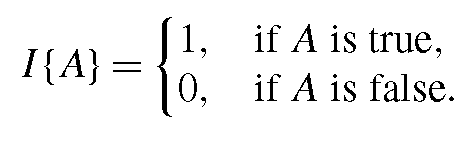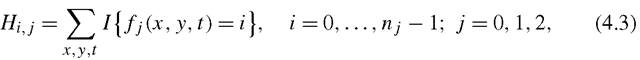The aim of this topic is to give a comprehensive overview of different facial representations and in particular describe local facial features.
Introduction
Developing face recognition systems involves two crucial issues: facial representation and classifier design [47,101]. The aim of facial representation is to derive a set of features from the raw face images which minimizes the intra-class variations (i.e., within face instances of a same individual) and maximizes the extra-class variations (i.e., between face images of different individuals). Obviously, if inadequate facial representations are adopted, even the most sophisticated classifiers fail to accomplish the face recognition task. Therefore, it is important to carefully decide on what facial representation to adopt when designing face recognition systems. Ideally, the facial feature representation should: (i) discriminate different individuals well while tolerating within-class variations; (ii) be easily extracted from the raw face images in order to allow fast processing; and (iii) lie in a low dimensional space (short vector length) in order to avoid a computationally expensive classifier. Naturally, it is not easy to find features which meet all these criteria because of the large variability in facial appearances due to different imaging factors such as scale, orientation, pose, facial expressions, lighting conditions, aging, presence of glasses, etc. These considerations are important for the other subtasks in face biometrics: detection, localization and registration, and verification, and thus, a key issue in face recognition is finding efficient facial feature representations.
Numerous methods have been proposed in literature for representing facial images for recognition purposes. The earliest attempts, such as Kanade’s work in early 70s [41], are based on representing faces in terms of geometrical relationships, such as distances and angles, between the facial landmarks (eyes, mouth etc.). Later, appearance based techniques have been proposed. These methods generally consider a face as a 2D array of pixels and aim at deriving descriptors for face appearance without explicit use of face geometry. Following these lines, different holistic methods such as Principal Component Analysis (PCA) [82], Linear Discriminant Analysis (LDA) [21] and the more recent 2D PCA [92] have been widely studied. Lately local descriptors have gained an increasing attention due to their robustness to challenges such as pose and illumination changes. Among these descriptors are Gabor filters and Local Binary Patterns [2] which are shown to be very successful in encoding facial appearance.
Structure and Scope of the topic
The aim of this topic is to give a comprehensive overview of different facial representations and in particular describe local facial features. Section 4.2 discusses the major methods which have been proposed in literature. Then, more detailed descriptions of two widely used approaches, namely local binary patterns and Gabor filters, are presented in Sects. 4.3 and 4.4, respectively. Section 4.5 discusses related issues and promising directions. Finally, concluding remarks are drawn in Sect. 4.6.
The methods discussed in this topic can be applied to detection and recognition of faces or face parts (landmarks). Face parts are also referred to as facial features, but we use the terms feature and facial feature interchangeably for any features extracted from the face area. We specifically discuss local binary patterns in the context of face recognition and Gabor features in the context of face part detection, but they can be used in the both tasks. Furthermore, the feature extraction methods are discussed from the face image processing point of view and other face description methods are available for the modeling purposes, such as the active shape models and morphable model described in the following topics. These novel modeling methods can also be applied to face recognition without explicit feature extraction and classification as discussed in this topic.
Review of Facial Feature Representations
We first justify and restrict the scope of this topic to generic features which do not require optimization or learning stages and then proceed to the actual review.
Zhao et al. [101] divide face recognition algorithms into (i) appearance-based (holistic), (ii) feature-based, and (iii) hybrid approaches. This taxonomy is widely accepted and also applies to face detection, localization and verification algorithms [33]. This topic specifically focuses on the feature-based and hybrid methods which utilize representations of local face parts. Zhao et al. further divide the feature-based and hybrid approaches into: (1) generic methods based on generic image processing features, such as edges, lines, curves, etc.; (2) feature-template-based methods that are used to detect specific facial features such as eyes, nostrils, etc.; and (3) structural matching methods that take into consideration geometrical constraints on the features. From the feature extraction point of view, the holistic approach and the feature-template-based methods are equivalent. They both learn a scanning window template or templates to represent and detect faces or facial parts. The most popular solutions are Viola-Jones detector [85] and PCA or LDA computed subspace-templates (Eigenfaces or Fisherfaces) [9] and their seminal works. These methods can be effective, but we do not include the Haar-cascades produced by the Viola-Jones method or subspace templates produced by the PCA and LDA to this topic since they are not generic features. They should be considered as learned statistical or algorithmic detectors themselves. Subspace methods are discussed in Chap. 3 and Viola-Jones type boosted detectors in Chap. 11. The Haar-like features used by the Viola-Jones detector, however, are generic features for facial feature representation. The structural matching methods are not in the scope either since they too involve the learning stage for a “constellation model” which captures information about spatial relationships between local features. Typical examples are active shape models, discussed in Chap. 4, and the Elastic Bunch Graph Matching (EBGM) [89]. The generic low level features used by these methods, however, belong to this topic.
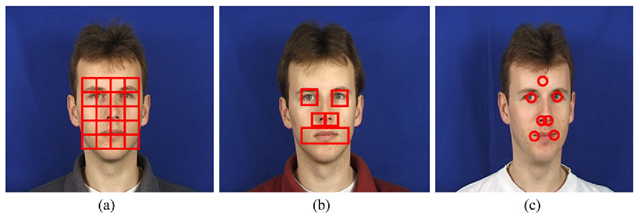
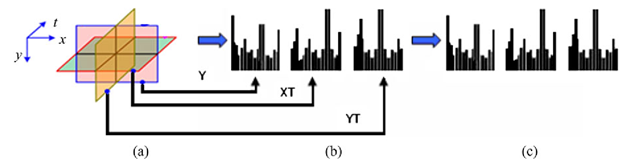
The selection of features for a proper facial feature representation is actually similar to the feature selection and extraction task occurring in the most computer vision and image analysis applications. But what features are the most suitable for face biometrics? The best results have been achieved by concatenating and learning person specific features computed from several local areas, for example, from fixed area (Fig. 4.1(a)) or varying area regions (Fig. 4.1(b)) which can be regular or feature-driven, or simply at specific locations with no strictly defined spatial extent (Fig. 4.1(c)). As already mentioned, implementations based on the subspace approach [11] and the boosted Haar-like features [103] for face detection and recognition exist, but they are not included here due to their need of task-specific learning.
Computer vision and image processing literature contains numerous features and feature extraction methods. In face biometrics, however, certain features retain their popularity and continuously succeed to producing state-of-the-art results for various benchmarks. Widely adopted are features constructed from responses of Gabor filters on various orientations and scales. More recent, and particularly successful, are local binary pattern (LBP) features.
Fig. 4.1 Facial feature computation from a a regular grid of fixed size regions, b irregular variable size regions (feature-driven) and c around central feature locations
In order to verify their status and to spot new trends, we reviewed the recently published feature-intense articles in the top tier forums of computer vision and face biometrics. A short summary of the review is presented in Table 4.1. We draw the following conclusions: (1) Gabor filters and other similar “local oriented frequency approaches” are still a popular choice and produce state-of-the-art results in face detection and recognition; (2) a new feature appears in the literature: the SIFT descriptor which is popular in visual object categorization and baseline matching; (3) gray-level patch remains as a popular choice as well despite of its extreme simplicity; and finally (4) success of LBP in biometrics promotes other similar algorithmically constructed features. An interesting work is the method by Xu et al. [90], which uses several different kind of features on different processing levels in their hierarchical system.
The most popular region features, modular PCA, LBP and Gabor magnitudes, were compared for face recognition in [103]. The LBP and Gabor features produced good results and were generally recommended. In Table 4.1, we classify many features, such as complex and smooth wavelets, steerable filters and difference of Gaus-sians, to Gabor-based methods, because there is no fundamental difference between them and properly utilized they should lead to equally good results. Similarly, SIFT, LBP and Daugman’s phase descriptor have similar characteristics. The flexibility of LBP features, however, makes them more suitable and preferable for face biometrics. The flexibility, appearing as various intuitive parameterizations and extensions to the standard LBP are further discussed in Sect. 4.3. The Haar-like features seem to succeed for the boosting approaches, but as a generic method for face biometrics there is no clear evidence for their success. Their accuracy to locate different facial landmarks have been studied in [11] and recently, other kind of features, such as anisotropic Gaussian [60] or constructed features [87], have succeeded in the boosting scheme.
It is clear from all previously published surveys and from the recent state-of-the-art results that the three mentioned features pop up as very popular and successful: features based on Gabor filter responses, local binary patterns (LBPs) and Haar-like features. Since the Haar-like features are covered in Chap. 11, this topic introduces the remaining two and presents results from face recognition and facial feature localization experiments.
Table 4.1 Feature-based methods for face detection and/or recognition. Papers utilizing LBP are numerous and therefore not included here but in Sect. 4.3
|
# |
Ref. |
Feature(s) |
Comment |
|
1 |
Zhang et al. [98] |
“Local derivative pattern” |
Similar to LBP |
|
2 |
Kozakaya et al. [42] |
Histogram of gradients (HOG) |
Similarto SIFT |
|
3 |
Zhang and Wang [94] |
SIFT |
|
|
4 |
Su et al. [77] |
Gabor |
Reg. grid, magn. only |
|
5 |
Pinto et al. [68] |
Gabor, Patch |
Magn. only, post-processing |
|
6 |
Hua and Akbarzadeh [34] |
Gradient descriptor in [88] |
|
|
7 |
Lee et al. [46] |
Modular PCA |
|
|
8 |
Liu and Dai [53] |
Wavelet |
Similar to Gabor |
|
9 |
McCool and Marcel [56] |
DCT coeffs. |
Similar to Gabor magn. histogram |
|
10 |
Ashraf et al. [7] |
Patch |
|
|
11 |
Ding and Martinez [19] |
Patch and geometric |
|
|
12 |
Liang et al. [50] |
Patch |
|
|
13 |
Meyers and Wolf [59] |
Gabor |
V1 type post-processing |
|
14 |
Mian et al. [61] |
3D descriptor and SIFT |
|
|
15 |
Xu et al. [90] |
Patch, gradient (AAM) and geometric |
Fusion over layers of processing |
|
16 |
Yan et al. [91] |
Haar based pattern (LAB) |
Similar to LBP |
|
17 |
Gokberk et al. [27] |
Gabor |
Magn. only, centroids |
|
18 |
Shastri and Levine [75] |
Non-negative sparse codebook |
Similar to Gabor magn. |
|
19 |
Zhang et al. [97] |
Gabor |
Daugman’s phase code [18] (similar to SIFT) |
|
20 |
Arca et al. [6] |
Gabor |
Magn. only, centroids |
|
21 |
Bicego et al. [10] |
SIFT |
|
|
22 |
Ekenel and Stiefelhagen [20] |
DCT coeffs. |
Similar to Gabor magn. histogram |
|
23 |
Zhang and Jia [93] |
Steerable filters |
Similar to Gabor |
|
24 |
Dalal and Triggs [14] |
Histogram of gradients (HOG) |
Similar to SIFT |
Local Binary Patterns
The use of local binary patterns in face analysis started in 2004 when a novel facial representation for face recognition was proposed [1, 2]. In this approach, the face image is divided into several regions from which the LBP features are extracted and concatenated into an enhanced feature histogram which is used as a face descriptor.
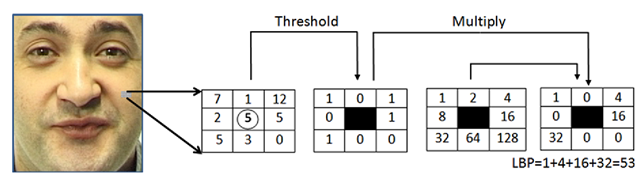
Fig. 4.2 The basic LBP operator
The approach has evolved to be a growing success and has been adopted and further developed by a large number of research groups and companies around the world. The LBP operator and its variants have been used not only in face recognition but also in various other face-related problems such as face detection, facial expression recognition, gender classification, age estimation and visual speech recognition. The success of LBP in face description is due to the discriminative power and computational simplicity of the operator, and its robustness to monotonic gray scale changes caused by, for example, illumination variations. The use of histograms as features also makes the LBP approach robust to face misalignment and pose variations. The Matlab code of the LBP operators can be found and freely downloaded from http://www.ee.oulu.fi/mvg/page/downloads.
Local Binary Patterns
LBP in the Spatial Domain
The LBP texture analysis operator, introduced by Ojala et al. [63, 64], is defined as a gray-scale invariant texture measure, derived from a general definition of texture in a local neighborhood. It is a powerful texture descriptor and among its properties in real-world applications are its discriminative power, computational simplicity and tolerance against monotonic gray-scale changes.
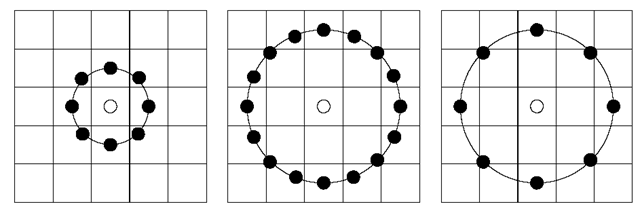
The original LBP operator forms labels for the image pixels by thresholding the 3 x 3 neighborhood with the center value and considering the result as a binary number. The histogram of these 28 = 256 different labels can then be used as an image descriptor. See Fig. 4.2 for an illustration of the basic LBP operator. The operator has been extended to use neighborhoods of different sizes [64]. Using a circular neighborhood and bilinear interpolation at noninteger pixel coordinates allow any radius and number of sampling points. In the following, the notation (P, R) will be used for pixel neighborhoods which means P sampling points on a circle of radius R. See Fig. 4.3 for an example of circular neighborhoods.
Another extension to the original operator is the definition of so called uniform patterns [64]. This extension was inspired by the fact that some binary patterns occur more frequently than others in texture images. A local binary pattern is called uniform if the binary pattern contains at most two bitwise transitions from 0 to 1 or vice versa when the bit pattern is traversed circularly. For example, the patterns 00000000 (0 transitions), 01110000 (2 transitions) and 11001111 (2 transitions) are uniform whereas the patterns 11001001 (4 transitions) and 01010011 (6 transitions) are not. In the computation of the LBP labels, uniform patterns are used so that there is a separate label for each uniform pattern and all the non-uniform patterns are labeled with a single label. For example, when using (8,R) neighborhood, there are a total of 256 patterns of which 58 are uniform thus yielding to the total of 59 different labels.
Fig. 4.3 Neighborhood set for different (P, R). The pixel values are bilinearly interpolated whenever the sampling point is not in the center of a pixel
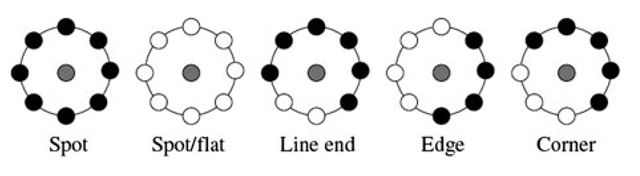
Fig. 4.4 Examples of texture primitives detected by LBP (white circles represent ones and black zeros)
Ojala et al. noticed in their experiments with texture images that uniform patterns account for almost 90% of all patterns when using the (8, 1) neighborhood and around 70% for the (16, 2) neighborhood. We have found that 90.6% of the patterns in the (8, 1) neighborhood and 85.2% of the patterns in the (8, 2) neighborhood are uniform in the case of preprocessed FERET face images [67]. Each LBP code can be regarded as a micro-texton. Local primitives which are codified by these bins include different types of curved edges, spots, flat areas etc. as illustrated in Fig. 4.4.
We use the following notation for the LBP operator: LBPp2s. The subscript denotes the operator in a (P, R) neighborhood. Superscript u2 stands for uniform patterns of maximum of 2 transitions and labeling all remaining patterns with a single label.
After the LBP labeled image fi(x, y) has been obtained, the LBP histogram can be defined as
in which n is the number of different labels produced by the LBP operator and
Fig. 4.5 a Three planes of dynamic texture; b LBP histograms of each plane; c Concatenated feature
When the image patches whose histograms are to be compared have different sizes, the histograms must be normalized to get a coherent description:
Spatiotemporal LBP
The original LBP operator was defined to only deal with the spatial information, but recently it has been extended to a spatiotemporal representation for dynamic texture (DT) analysis. This has yielded to so called Volume Local Binary Pattern operator (VLBP) [99]. The idea behind VLBP consists of looking at dynamic texture as a set of volumes in the (X,Y,T)-space where X and Y denote the spatial coordinates and T the frame index (time). The neighborhood of each pixel is thus defined in a three dimensional space. Then, similarly to LBP, volume textons can be defined and extracted into histograms. Therefore, VLBP combines motion and appearance into a dynamic texture description.
To make the VLBP computationally simple and easy to extend, the cooccurrences of the LBP on the three orthogonal planes (LBP-TOP) was introduced [99]. LBP-TOP consists of the three orthogonal planes: XY, XT and YT, and concatenating local binary pattern co-occurrence statistics in these three directions. The circular neighborhoods are generalized to elliptical sampling to fit to the space-time statistics. The LBP codes are extracted from the XY, XT and YT planes, denoted as XY-LBP, XT-LBP and YT-LBP, for all pixels, and statistics of the three different planes are concatenated into a single histogram. The procedure is shown in Fig. 4.5. In this representation, dynamic texture (DT) is encoded by XY-LBP, XT-LBP and YT -LBP.
Using equal radii for the time and spatial axes is not reasonable for dynamic textures [99] and therefore, in the XT and YT planes, different radii can be assigned to sample neighboring points in space and time. More generally, the radii in axes X, Y and T, and the number of neighboring points in the XY, XT and YT planes can also be different denoted by Rx, Ry and Rt, Pxy, Pxt and Pyt. The corresponding feature is denoted as LBP-TOPPxy,PxTiPyt,RxiRyiRt.
Let us assume we are given an X x Y x T dynamic texture![]()
![]() A histogram of the DT can be defined as
A histogram of the DT can be defined as
in which nj is the number of different labels produced by the LBP operator in the jth plane (j = 0 : XY, 1 : XT and 2 : YT) and fi(x,y,t) expresses the LBP code of central pixel (x,y,t) in the j th plane. Similarly to the original LBP, the histograms must be normalized to get a coherent description for comparing the DTs:
Multi-Scale LBP
Noticing that LBP features calculated in a local 3 x 3 neighborhood cannot capture large-scale structures, multi-scale LBP has been proposed to overcome this limitation. A straightforward way of enlarging the spatial support area is to combine the information provided by N LBP operators with varying P and R values. This way, each pixel in an image gets N different LBP codes. The most accurate information would be obtained by using the joint distribution of these codes. However, such a distribution would be overwhelmingly sparse with any reasonable image size. Therefore, only the marginal distributions of the different operators are considered. Even though the LBP codes at different radii are not statistically independent in the typical case, using multi-resolution analysis often enhances the discriminative power of the resulting features. With most applications, this straightforward way of building a multi-scale LBP operator has resulted in very good accuracy.
An extension of multi-scale LBP operator is the multiscale block local binary pattern (MB-LBP) [51] which has gained popularity especially in facial image analysis. The key idea of MB-LBP is to compare average pixel values within small blocks instead of comparing pixel values. The operator always considers 8 neighbors, producing labels from 0 to 255. For instance, if the block size is 3 x 3 pixels, the corresponding MB-LBP operator compares the average gray value of the center block to the average values of the 8 neighboring blocks of the same size and the effective area of the operator is 9 x 9 pixels.