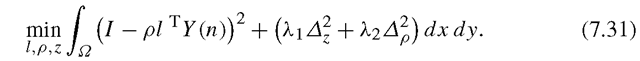Enforcing Nonnegative Light
When we take arbitrary linear combinations of the harmonic basis images, we may obtain images that are not physically realizable. This is because the corresponding linear combination of the harmonics representing lighting may contain negative values. That is, rendering these images may require negative “light,” which of course is physically impossible. In this section, we show how to use the basis images while enforcing the constraint of nonnegative light.
When we use a 9D approximation to an object’s images, we can efficiently enforce the nonnegative lighting constraint in a manner similar to that proposed by Belhumeur and Kriegman [9], after projecting everything into the appropriate 9D linear subspace. Specifically, we approximate any arbitrary lighting function as a nonnegative combination of a fixed set of directional light sources. We solve for the best such approximation by fitting to the query image a nonnegative combination of images each produced by a single, directional source.
We can do this efficiently using the 9D subspace that represents an object’s images. We project into this subspace a large number of images of the object, in which each image is produced by a single directional light source. Such a light source is represented as a delta function; we can derive the representation of the resulting image in the harmonic basis simply by taking the harmonic transform of the delta function that represents the lighting. Then we can also project a query image into this 9D subspace and find the nonnegative linear combination of directionally lit images that best approximate the query image. Finding the nonnegative combination of vectors that best fit a new vector is a standard, convex optimization problem. We can solve it efficiently because we have projected all the images into a space that is only 9D.
Note that this method is similar to that presented in Georghiades et al. [18]. The primary difference is that we work in a low dimensional space constructed for each model using its harmonic basis images. Georghiades et al. performed a similar computation after projecting all images into a 100-dimensional space constructed using PCA on images rendered from models in a 10-model database. Also, we do not need to explicitly render images using a point source and project them into a low dimensional space. In our representation, the projection of these images is given in closed form by the spherical harmonics.
A further simplification can be obtained if the set of images of an object is approximated only up to first order. Four harmonics are required in this case. One is the DC component, representing the appearance of the object under uniform ambient light, and three are the basis images also used by Shashua. In this case, we can reduce the resulting optimization problem to one of finding the roots of a sixth degree polynomial in a single variable, which is extremely efficient. Further details of both methods can be found elsewhere [6].
The approach of enforcing nonnegative lighting for 9 harmonics relies on representing lighting as the nonnegative sum of a large number of delta functions. In this way, the nonnegativity of the lighting follows from the nonnegativity of the coefficients of the delta functions. However, in recent work, Shirdhonkar and Jacobs [41] have shown that nonnegativity can be enforced when representing lighting using low frequency spherical harmonics. To do this, one must be able to determine whether a set of low frequency spherical harmonics are consistent with a nonnegative function; that is, could one add higher frequency harmonics to make the complete function nonnegative. By extending Szego’s eigenvalue distribution theorem to spherical harmonics, Shirdhonkar and Jacobs show that a matrix constructed using the coefficients of low frequency lighting, represented as spherical harmonics, must be positive semi-definite in order for these harmonics to be consistent with non-negative lighting. This allows them to compute the low frequency lighting that best matches a 3D model to an image by solving a semi-definite programming problem. This leads to solutions that are more accurate and efficient than previous methods that represent lighting using delta functions.
Specularity
Other work has built on this spherical harmonic representation to account for non-Lambertian reflectance [36]. The method first computes Lambertian reflectance, which constrains the possible location of a dominant compact source of light. Then it extracts highlight candidates as pixels that are brighter than we can predict from Lambertian reflectance. Next, we determine which of these candidates is consistent with a known 3D object. A general model of specular reflectance is used that implies that the surface normals of specular points obtained by thresholding intensity form a disk on the Gaussian sphere. Therefore, the method proceeds by selecting candidate specularities consistent with such a disk. It maps each candidate specularity to the point on the sphere having the same surface normal. Next, a plane is found that separates the specular pixels from the other pixels with a minimal number of misclassifications. The presence of specular reflections that are consistent with the object’s known 3D structure then serves as a cue that the model and image match.
This method has succeeded in recognizing shiny objects, such as pottery. However, informal face recognition experiments with this method, using the data set described in the next section, have not shown significant improvements. Our sense is that most of our recognition errors are due to misalignments in pose, and that when a good alignment is found between a 3D model and image a Lambertian model is sufficient to produce good performance on a data set of 42 individuals.
In other work, Georghiades [16] augmented the recognition approach of Georghi-ades et al. [17] to include specular reflectance. After initialization using a Lambertian model, the position of a single light source and parameters of the Torrance-Sparrow model of specular reflectance are optimized to fit a 3D model of an individual. Face recognition experiments with a data set of 10 individuals show that this produces a reduction in overall errors from 2.96% to 2.47%. It seems probable that experiments with data sets containing large numbers of individuals are needed to truly gauge the value of methods that account for specular reflectance.
Experiments
We have experimented with these recognition methods using a database of faces collected at NEC in Japan. The database contains models of 42 faces, each including the 3D shape of the face (acquired using a structured light system) and estimates of the albedos in the red, green, and blue color channels. As query images, we use 42 images each of 10 individuals taken across seven poses and six lighting conditions (shown in Fig. 7.5). In our experiment, each of the query images is compared to each of the 42 models, and then the best matching model is selected.
In all methods, we first obtain a 3D alignment between the model and the image using the algorithm of Blicher and Roy [10]. In brief, a dozen or fewer features on the faces were identified by hand, and then a 3D rigid transformation was found to align the 3D features with the corresponding 2D image features.
In all methods, we only pay attention to image pixels that have been matched to some point in the 3D model of the face. We also ignore image pixels that are of maximum intensity, as they may be saturated and provide misleading values. Finally, we subsample both the model and the image, replacing each m x m square with its average values. Preliminary experiments indicate that we can subsample quite a bit without significantly reducing accuracy. In the experiments below, we ran all algorithms subsampling with 16 x 16 squares, while the original images were 640 x 480.
Fig. 7.5 Test images used in the experiments
Our methods produce coefficients that tell us how to combine the harmonic images linearly to produce the rendered image. These coefficients were computed on the sampled image but then applied to harmonic images of the full, unsampled image. This process was repeated separately for each color channel. Then a model was compared to the image by taking the root mean squared error derived from the distance between the rendered face model and all corresponding pixels in the image.
Figure 7.6 shows performance curves for three recognition methods: the 9D linear method and the methods that enforce positive lighting in 9D and 4D. The curves show the fraction of query images for which the correct model is classified among the top k, as k varies from 1 to 40. The 4D positive lighting method performs significantly less well than the others, getting the correct answer about 60% of the time. However, it is much faster and seems to be quite effective under simpler pose and lighting conditions. The 9D linear method and 9D positive lighting method each pick the correct model first 86% of the time. With this data set, the difference between these two algorithms is quite small compared to other sources of error. Such errors may include limitations in our model for handling cast shadows and specu-larities, but they also include errors in the model building and pose determination processes. In fact, on examining our results, we found that one pose (for one person) was grossly wrong because a human operator selected feature points in the wrong order. We eliminated from our results the six images (under six lighting conditions) that used this pose.
Fig. 7.6 Performance curves for our recognition methods. The vertical axis shows the percentage of times the correct model was found among the k best matching models; the horizontal axis shows k
Modeling
The recognition methods described in the previous section require detailed 3D models of faces, as well as their albedos. Such models can be acquired in various ways. For example, in the experiments described above we used a laser scanner to recover the 3D shape of a face, and we estimated the albedos from an image taken under ambient lighting (which was approximated by averaging several images of a face). As an alternative, it is possible to recover the shape of a face from images illuminated by structured light or by using stereo reconstruction, although stereo algorithms may give somewhat inaccurate reconstructions for nontextured surfaces. Finally, other studies have developed reconstruction methods that use the harmonic formulation to recover both the shape and the albedo of an object simultaneously. In the remainder of this section, we briefly describe three such methods. We first describe how to recover the shape of an object when the input images are obtained with a stationary object illuminated by variable lighting, a problem commonly referred to as “photometric stereo.” Later, we discuss an approach for shape recovery of a moving object. We conclude with an approach that can recover the shape of faces from single images by exploiting prior knowledge of the generic shape of faces.
Photometric Stereo
In photometric stereo, we are given a collection of images of a stationary object under varying illumination. Our objective is to recover the 3D shape of the object and its reflectance properties, which for a Lambertian object include the albedo at every surface point. Previous approaches to photometric stereo under unknown lighting generally assume that in every image the object is illuminated by a dominant point source for example, [20, 28, 47]. However, by using spherical harmonic representations it is possible to reconstruct the shape and albedo of an object under unknown lighting configurations that include arbitrary collections of point and extended sources. In this section, we summarize this work, which is described in more detail elsewhere [5, 7].
We begin by stacking the input images into a matrix M of size f x p, in which every input image of p pixels occupies a single row, and f denotes the number of images in our collection. The low dimensional harmonic approximation then implies that there exist two matrices, L and S, of sizes f x r and r x p respectively, that satisfy
where L represents the lighting coefficients, S is the harmonic basis, and r is the dimension used in the approximation (usually 4 or 9). If indeed we can recover L and S, obtaining the surface normals and albedos of the shape is straightforward using (7.23) and (7.26).
We can attempt to recover L and S using singular value decomposition (SVD). This produces a factorization of M into two matrices L and Si, which are related to the correct lighting and shape matrices by an unknown, arbitrary r x r ambiguity matrix A. We can try to reduce this ambiguity. Consider the case that we use a first-order harmonic approximation (r = 4). Omitting unnecessary scale factors, the zero-order harmonic contains the albedo at every point, and the three first-order harmonics contain the surface normal scaled by the albedo. For a given point we can write these four components in a vector: p = (ρ, pnx,pny,pnz)T. Then p should satisfy pT Jp = 0, where J = diag{— 1, 1,1, 1}. Enforcing this constraint reduces the ambiguity matrix from 16 degrees of freedom to just 7. Further resolution of the ambiguity matrix requires additional constraints, which can be obtained by specifying a few surface normals or by enforcing integrability.
A similar technique can be applied in the case of a second order harmonic approximation (r = 9). In this case, there are many more constraints on the nine basis vectors, and they can be satisfied by applying an iterative procedure. Using the nine harmonics, the surface normals can be recovered up to a rotation, and further constraints are required to resolve the remaining ambiguity.
An application of these photometric stereo methods is demonstrated in Fig. 7.7. A collection of 32 images of a statue of a face illuminated by two point sources in each image were used to reconstruct the 3D shape of the statue. (The images were simulated by averaging pairs of images obtained with single light sources taken by researchers at Yale.) Saturated pixels were removed from the images and filled in using Wiberg’s algorithm [46]; see also [23,42]. We resolved the remaining ambiguity by matching some points in the scene with hand-chosen surface normals.
Photometric stereo is one way to produce a 3D model for face recognition. An alternative approach is to determine a discrete set of lighting directions that produce a set of images that span the 9D set of harmonic images of an object. In this way, the harmonic basis can be constructed directly from images, without building a 3D model. This problem was addressed by Lee et al. [31] and by Sato et al. [39]. Other approaches use harmonic representations to cluster the images of a face under varying illumination [22] or determine the harmonic images of a face from just one image using a statistical model derived from a set of 3D models of other faces [49].
Fig. 7.7 Left: three images of a bust illuminated each by two point sources. Right: the surface produced by the 4D method.
Objects in Motion
Photometric stereo methods require a still object while the lighting varies. For faces, this requires a cooperative subject and controlled lighting. An alternative approach is to use video of a moving face. Such an approach, presented by Simakov et al. [43], is briefly described below.
We assume that the motion of a face is known, for example, by tracking a few feature points such as the eyes and the tips of the mouth. Thus, we know the epipolar constraints between the images and (in case the cameras are calibrated) also the mapping from 3D to each of the images. To obtain a dense shape reconstruction, we need to find correspondences between points in all images. Unlike stereo, in which we can expect corresponding points to maintain approximately the same intensity, in the case of a moving object we expect points to change their intensity as they turn away from or toward light sources.
We therefore adopt the following strategy. For every point in 3D, we associate a “correspondence measure,” which indicates if its projections in all the images could come from the same surface point. To this end, we collect all the projections and compute the residual of the following set of equations.
In this equation,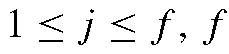
is the number of images, Ij denotes the intensity of the projection of the 3D point in the jth image, ρ is the unknown albedo, l denotes the unknown lighting coefficients, Rj denotes the rotation of the object in the j th image, and Y(n) denotes the spherical harmonics evaluated for the unknown surface normal. Thus, to compute the residual we need to find l and n that minimize the difference between the two sides of this equation. (Note that for a single 3D point ρ and l can be combined to produce a single vector.)
Once we have computed the correspondence measure for each 3D point, we can incorporate the measure in any stereo algorithm to extract the surface that minimizes the measure, possibly subject to some smoothness constraints.
The algorithm of Simakov et al. [43] described above assumes that the motion between the images is known. Zhang et al. [48] proposed an iterative algorithm that simultaneously recovers the motion assuming infinitesimal motion between images and modeling reflectance using a first order harmonic approximation.
Reconstruction with Shape Prior
While the previous methods utilize collections of images to achieve 3D reconstruction, it is of interest to explore methods that can recover the shape of faces from just a single image. Recently, Kemelmacher-Shlizerman and Basri [26, 27] proposed such an approach that exploits prior knowledge of the rough shape of faces to make the problem of single view reconstruction well-posed.
The algorithm obtains as input an image of a face to be reconstructed along with a 3D model (shape and albedo) of some different face. Such a model can depict an individual whose 3D shape is available, or an “averaged” model of a collection of faces. The algorithm then attempts to reconstruct the shape of the face in the input image essentially by solving a shape from shading (SFS) problem. However, while SFS is ill-posed and its solution requires knowledge of the lighting conditions, the reflectance properties (albedo) of the object to be reconstructed, and boundary conditions (i.e., depth values at extremal points), this algorithm estimates their values by exploiting the similarity of the input model to the desired shape.
Specifically, Kemelmacher-Shlizerman and Basri seek a solution to the following optimization problem:
In this expression, I(x,y) is the input image
l represents the unknown lighting conditions, ρ(x, y) the unknown albedo, z(x, y) the unknown depth, and Y(n) the spherical harmonic basis derived from z. The first term therefore is a data term fitting the desired reconstruction to the image. For the second term, λχ and λ2 are preset constants and we define
to represent respectively, the (smoothed) difference in shape and albedo between the desired shape and the input model. The role of this regularization term is to keep those differences small. Figure 7.8 shows a reconstruction obtained with this method.
Conclusions
Lighting can be arbitrarily complex, but in many cases its effect is not. When objects are Lambertian, we show that a simple, 9D linear subspace can capture the set of images they produce.
Fig. 7.8 Single view reconstruction. The figure shows two triplets of images; each includes an input image, 3D reconstruction (output), and the input image overlayed on the reconstruction. The reference shape used in these runs is shown on the right. Notice that veridical shape is recovered despite change in expression relative to the reference shape.
This explains prior empirical results. It also gives us a new and effective way to understand the effects of Lambertian reflectance as that of a low-pass filter on lighting.
Moreover, we show that this 9D space can be directly computed from a model, as low-degree polynomial functions of its scaled surface normals. This description allows us to produce efficient recognition algorithms in which we know we are using an accurate approximation of the model’s images. In addition, we can use the harmonic formulation to develop reconstruction algorithms to recover the 3D shape and albedos of an object. We evaluate the effectiveness of our recognition algorithms using a database of models and images of real faces.
Acknowledgements Major portions of this research were conducted while Ronen Basri and David Jacobs were at the NEC Research Institute, Princeton, NJ. At the Weizmann Institute Ronen Basri is supported in part by European Community grants IST-2000-26001 VIBES and IST-2002-506766 Aim Shape and by the Israel Science Foundation grant 266/02. The vision group at the Weizmann Institute is supported in part by the Moross Foundation. David Jacobs was funded by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), through the Army Research Laboratory (ARL). All statements of fact, opinion or conclusions contained herein are those of the authors and should not be construed as representing the official views or policies of IARPA, the ODNI, or the U.S. Government.
