Facial Action Tracking (Face Recognition Techniques) Part 2

Parameter Estimation Using an Extended Kalman Filters

A Kalman filter is used to estimate the dynamic changes of a state vector of which a function can be observed. When the function is nonlinear, we must use an extended Kalman filter (EKF). The literature on Kalman filtering is plentiful [21, 28, 54, 55], so we only summarize the approach here.

In our case, the state vector is the model parameter vector p and we observe, for each frame, the screen coordinatesBecause we cannot measure the screen coordinates exactly, measurement noise vk is added as well. We can summarize the dynamics of the system as

whereis the dynamics function,is the measurement function, and w and v are zero-mean Gaussian random variables with known covariances

The job for the EKF is to estimate the state vector pk given the measurement vectorand the previous estimateChoosing the trivial dynamics function the state estimate is updated using

whereis the Kalman gain matrix. It is updated every time step depending on The covariances are given by initial assumptions or estimated during the tracking.

Tracking Process

The tracker must be initialized, manually or by using a face detection algorithm. The model reference texture is captured from the first frame, and feature points are automatically extracted. To select feature points that could be reliably tracked, points where the determinant of the Hessian

is large are used. The function cv Good Features To Track in Open CV [44] implements a few variations. The determinant is weighted with the cosine of the angle between the model surface normal and the camera direction. The number of feature points to select is limited only by the available computational power and the real-time requirements.

The initial feature point depth values (zi,…,zN) are given by the 3D face model. Then, for each frame, the model is rendered using the current model parameters. Around each feature point, a small patch is extracted from the rendered image.

Fig. 18.3 Patches from the rendered image (lower left) are matched with the incoming video. The two-dimensional feature point positions are fed to the EKF, which estimates the pose information needed to render the next model view. For clarity, only 4 of 24 patches are shown.

The patches are matched with the new frame using a zero-mean normalized cross correlation. The best match, with subpixel precision, for each feature point is collected in the measurement vector uk and fed into the EKF update equation (18.21).

Using the face model and the values from the normalized template matching, the measurement noise covariance matrix can be estimated making the EKF rely on some measurements more than others. Note that this also tells the EKF in which directions in the image the measurements are reliable. For example, a feature point on an edge (e.g., the mouth outline) can reliably be placed in the direction perpendicular to the edge but less reliably along the edge. The system is illustrated in Fig. 18.3.

Tracking of Facial Action

Ingemars and Ahlberg [24] extended the tracker to track facial action as well. A set of states was added to the state vector corresponding to the animation parameters of Candide-3. In order to be able to track these, there must be feature points within the area that is influenced by each estimated animation parameter, and the number of feature points must be higher. However, the automatic feature point selection can still be used, since the observation function can be calculated online by interpolation of the known observation functions of the face model vertices.

In order to be both accurate and to handle drift, the tracker combines feature point patches from the first frame of the sequence with patches dynamically extracted from the previous frame. Examples are shown in Fig. 18.4.

Fig. 18.4 Tracking example, feature-based tracking. The leftmost image shows the automatically extracted tracking points.

Appearance-Based Tracking Example

In this section, we describe a statistical model-based and appearance-based tracker estimating the 3D pose and deformations of the face. It is based on the Active Appearance Models (AAMs) described in Chap. 5. The tracker was first presented by Ahlberg [1], and was later improved in various ways as described in Sect. 18.5.4.

To use the AAM search algorithm, we must first decide on a geometry for the face model, its parameterization of shape and texture, and how we use the model for warping images. Here, we use the face model Candide-3 described in Sect. 18.2.5.

Face Model Parameterization

Geometry Parameterization

The geometry (structure) g^, a) of the Candide model is parameterized according to (18.7). There are several techniques to estimate the shape parameters σ (e.g., an AAM search or facial landmark localization method). When adapting a model to a video sequence, the shape parameters should be changed only in the first frame(s)— the head shape does not vary during a conversation—whereas the pose and animation parameters naturally change at each frame. Thus, during the tracking process we can assume that σ is fixed (and known), and let the shape depend on a only

Pose Parameterization

To perform global motion (i.e., pose change), we need six parameters plus a scaling factor according to (18.8). Since the Candide model is defined only up to scale, we can adopt the weak perspective projection and combine scale and z-translation in one parameter. Thus, using the 3D translation vectorand    the three Euler angles for the rotation matrix R, our pose parameter vector is

Texture Parameterization

We use a statistical model of the texture and control the texture with a small set of texture parameters ξ. The model texture vector x is generated according to (18.1) (see Sect. 18.2.1). The synthesized texture vector x has for each element a corresponding (j, t) coordinate and is equivalent to the texture image It (j, t): the relation is just lexicographic ordering,is    mapped on the wireframe model to create the generated imageaccording    to    (18.5).

The entire appearance of the model can now be controlled using the parameters However, as we assume that the shape σ is fixed during the tracking session, and the texture ξ depends on the other parameters, the parameter vector we optimize below is

Tracking Process

The tracker should find the optimal adaptation of the model to each frame in a sequence as described in Sect. 18.3.3. That is, we wish to find the parameter vector pjj; that minimizes the distance between image Im generated by the model and each frame Ik. Here, an iterative solution is presented, and as an initial value of p we use pk—I (i.e., the estimated parameter vector from the previous frame).

Instead of directly comparing the generated image Im(u, v) to the input image Ik(u, v), we back-project the input image to the model’s parametric surface coordinate system (j, t) using the inverse of the texture mapping transform Tu

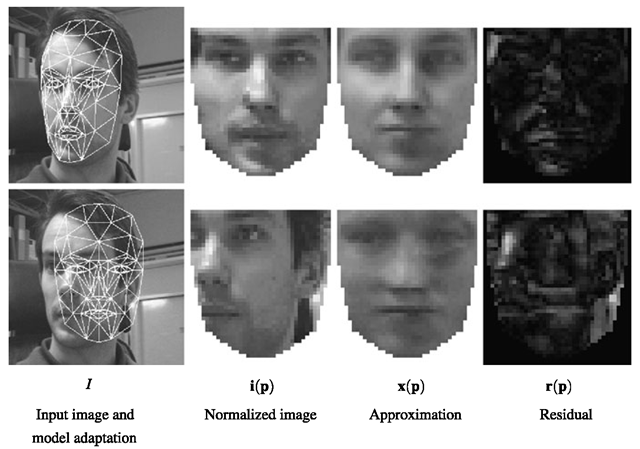
We then compare the normalized input image vector x(p) to the generated model texture vectoris generated in the face subspace as closely as possible to x(p) (see (18.1)), and we compute a residual imageThe process from input image to residual, is illustrated in Fig. 18.5.

As the distance measures according to (18.14), we use the squared norm of the residual image

From the residual image, we also compute the update vector

whereis    the precomputed active appearance update matrix (i.e., the

pseudo-inverse of the estimated gradient matrixIt is created by numeric differentiation, systematically displacing each parameter and computing an average over the training set.

Fig. 18.5 Analysis-synthesis process. A good and a bad model adaptation. The more similar the normalized image and its approximation is, the better the model adaptation is

We then compute the estimated new parameter vector as

In most cases, the model fitting is improved if the entire process is iterated a few times.

Tracking Example

To illustrate, a video sequence of a previously unseen person was used and the Candide-3 model was manually adapted to the first frame of the sequence by changing the pose parameters and the static shape parameters (recall that the shape parameter vector σ is assumed to be known). The model parameter vector p was then iteratively optimized for each frame, as is shown in Fig. 18.6.

Note that this, quite simple, tracker needs some more development in order to be robust to varying illumination, strong facial expressions, and large head motion. Moreover, it is very much depending on the training data.

Fig. 18.6 Tracking example, appearance-based tracking. Every tenth frame shown

Improvements

In 2002, Dornaika and Ahlberg [12, 13] introduced a feature/appearance-based tracker. The head pose is estimated using a RANdom SAmpling Consensus (RANSAC) technique [19] combined with a texture consistency measure to avoid drifting. Once the 3D head pose π is estimated, the facial animation parameters a can be estimated using the scheme described in Sect. 18.5.

In 2004, Matthews and Baker [37] proposed the Inverse Compositional Algorithm which allows for an accurate and fast fitting, actually reversing the roles of the input image and the template in the well-known, but slow, Lucas-Kanade Image Alignment algorithm [34]. Supposing that the appearance will not change much among different frames, it can be “projected out” from the search space. Fanelli and Fratarvangeli [18] incorporated the Inverse Compositional Algorithm in an AAM-based tracker to improve robustness.

Zhou et al. [65] and Dornaika and Davoine [15] combined appearance models with a particle filter for improved 3D pose estimation.

Fused Trackers

Combining Motion- and Model-Based Tracking

In order to exploit the advantages of the various tracking strategies mentioned above, modern state-of-the-art trackers often combine them. For example, Lefèvre and Odobez [32] used the Candide model and two sets of feature points. The first set is called the “trained set”, that is, a set of feature points trained from the first frame of the video sequence. The second set is the “adaptive set”, that is continuously adapted during tracking. Using only one of these sets (the first corresponding to first frame model-based and the second to motion-based, according to the terminology used here) results in a certain kinds of tracking failures. While tracking using the adaptive method (motion-based tracking) is more precise, it is also prone to drift. Lefèvre and Odobez devised a hybrid method exploiting the advantages of both the adaptive and the trained method. Compared to the method by Ingemars and Ahlberg [24] described above, Lefèvre and Odobez made a more thorough investigation of how to exploit the two methods. Another major difference is the choice of methods for 3D pose estimation from 2D measurements (EKF and Nelder-Mead downhill simplex optimization [42], respectively). Notably, Lefèvre and Odobez demonstrated stable tracking under varying lighting conditions.

Fig. 18.7 Face model alignment examples.

Combining Appearance- and Feature-Based Tracking

Another recent development was published by Caunce et al. [9], combining the feature-based and appearance-based approaches. In the tradition of the Manchester group (where the AAMs originated), the work was started with thorough statistical model-building of shape and texture of the face. Using profile and frontal photographies, a 3D shape model was adapted to each training subject and a PCA performed. A set of texture patches were extracted from the mean texture, and used to adapt the 3D model to a new image in a two stage process. The first stage consists of the rigid body adaptation (pose, translation) and the second step the facial shape (restrained by the pretrained model). Moreover, a scale hierarchy was used.

Thus, this method is primarily aimed at facial landmark localization/face model alignment, but is used (by Caunce et al.) for tracking of facial action as well by letting the parameter estimated from the previous frame serving as the initial estimation. Example results are shown in Fig. 18.7 using XM2VTSDB [38] imagery.

Commercially Available Trackers

Naturally, there are a number of commercial products providing head, face and facial action tracking. Below, some of these are mentioned.

One of the best commercial facial trackers was developed in the 1990s by a US company called Eyematic. The company went bankrupt and the technology was taken over by another company which subsequently sold it to Google.

The Australian company Seeing Machines is offering a face tracker API called faceAPI that tracks head motion, lips and eyebrows.

Visage Technologies (Sweden) provides a statistical appearance-based tracker as well as an feature-based tracker in an API called visage|SDK.

The Japanese company Omron developed a suite of face sensing technology called OKAO Vision that includes face detection, tracking of the face, lips, eyebrows and eyes, as well as estimation of attributes such as gender, ethnicity and age.

Image Metrics (UK) provides high-end performance-based facial animation service to film and game producers based on their in-house facial tracking algorithms.

Mova (US) uses a radically different idea in order to precisely capture high-density facial surface data using phosphorescent makeup and fluorescent lights.

Other companies with face tracking products include Genemation (UK), OKI (Japan), SeeStorm (Russia) and Visual Recognition (Netherlands). Face and facial feature tracking is also used in end-user products such as Fix8 by Mobinex (US) and the software bundled with certain Logitech webcams.

Conclusions

We have described some strategies for tracking and distinguished between model-and motion-based tracking as well as between appearance- and feature-based tracking. Whereas motion-based trackers may suffer from drifting, model-based trackers do not have that problem. Appearance- and feature-based trackers follow different basic principles and have different characteristics.

Two trackers have been described, one feature-based and one appearance-based. Both trackers are all model-based and thus do not suffer from drifting. Improvements found in the literature are discussed for both trackers.

Trackers combining the described tracking strategies, presumably representing the state-of-the-art, have been described, and commercially available tackers have been briefly mentioned.