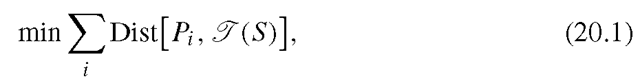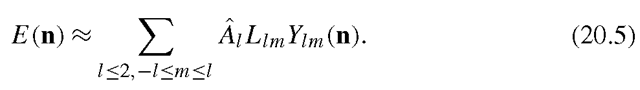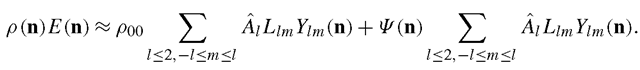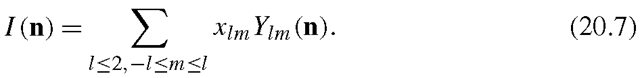Introduction
How to synthesize photorealistic images of human faces has been a fascinating yet difficult problem in computer graphics. Here, the term “face synthesis” refers to synthesis of still images as well as synthesis of facial animations. In general, it is difficult to draw a clean line between the synthesis of still images and that of facial animations. For example, the technique of synthesizing facial expression images can be directly used for generating facial animations, and most of the facial animation systems involve the synthesis of still images. In this topic, we focus more on the synthesis of still images and skip most of the aspects that mainly involve the motion over time.
Face synthesis has many interesting applications. In the film industry, people would like to create virtual human characters that are indistinguishable from the real ones. In games, people have been trying to create human characters that are interactive and realistic. There are commercially available products [18, 19] that allow people to create realistic looking avatars that can be used in chat rooms, email, greeting cards, and teleconferencing. Many human-machine dialog systems use realistic-looking human faces as visual representation of the computer agent that interacts with the human user. Face synthesis techniques have also been used for talking head compression in the video conferencing scenario.
The techniques of face synthesis can be useful for face recognition too. Romd-hani et al. [47, 48] used their three dimensional (3D) face modeling technique for face recognition with different poses and lighting conditions. Qing et al. [44] used the face relighting technique as proposed by Wen et al. [59] for face recognition under a different lighting environment. Wang et al. [57] used the 3D spherical harmonic morphable model (SHBMM), an integration of spherical harmonics into the morphable model framework, for face recognition under arbitrary pose and illumination conditions. Many face analysis systems use an analysis-by-synthesis loop where face synthesis techniques are part of the analysis framework.
In this topic, we review recent advances on face synthesis including 3D face modeling, face relighting, and facial expression synthesis.
Face Modeling
In the past a few years, there has been a lot of work on the reconstruction of face models from images [12, 23, 27, 41, 47, 52, 67]. There are commercially available software packages [18, 19] that allow a user to construct their personalized 3D face models. In addition to its applications in games and entertainment, face modeling techniques can also be used to help with face recognition tasks especially in handling different head poses (see Romdhani et al. [48] and Chap. 10). Face modeling techniques can be divided into three categories: face modeling from an image sequence, face modeling from two orthogonal views, and face modeling from a single image. An image sequence is typically a video of someone’s head turning from one side to the other. It contains a minimum of two views. The motion between each two consecutive views is relatively small, so it is feasible to perform image matching.
Face Modeling from an Image Sequence
Given an image sequence, one common approach for face modeling typically consists of three steps: image matching, structure from motion, and model fitting. First, two or three relatively frontal views are selected, and some image matching algorithms are used to compute point correspondences. The selection of frontal views are usually done manually. Point correspondences are computed either by using dense matching techniques such as optimal flow or feature-based corner matching. Second, one needs to compute the head motion and the 3D structures of the tracked points. Finally, a face model is fitted to the reconstructed 3D points. People have used different types of face model representations including parametric surfaces [13], linear class face scans [5], and linear class deformation vectors [34].
Fua and Miccio [13, 14] computed dense matching using image correlations. They then used a model-driven bundle adjustment technique to estimate the motions and compute the 3D structures. The idea of the model-driven bundle adjustment is to add a regularizer constraint to the traditional bundle adjustment formulation. The constraint is that the reconstructed 3D points can be fit to a parametric face model. Finally, they fit a parametric face model to the reconstructed 3D points. Their parametric face model contains a generic face mesh and a set of control points each controlling a local area of the mesh. By adjusting the coefficients of the control points, the mesh deforms in a linear fashion. Denote c1,c2,…,cm to be the coefficients of the control points. Let R, T, s be the rotation, translation, and scaling parameters of the head pose. Denote the mesh of the face as
Let
denote the transformation operator, which is a function of R, T,s. The model fitting can be formulated as a minimization problem
where Pi is the reconstructed 3D points, and Dist
is the distance from Pito the surface
This minimization problem can be solved using an iterative closest point approach. First, c1,…,cm are initialized and fixed. For each point Pi, find its closest point Qi on the surface S. Then solve for the pose parameters R,T,s to minimize 
by using the quaternion-based technique [17]. The head pose parameters are then fixed. Because S is a linear function of c1,…,cm, (20.1) becomes a linear system and can be solved through a least-square procedure. At the next iteration, the newly estimated c1,…,cm are fixed, and we solve for R, T, s again.
Liu et al. [32, 34] developed a face modeling system that allows an untrained user with a personal computer and an ordinary video camera to create and instantly animate his or her face model. The user first turns his or her head from one side to the other. Then two frames pop up, and the user is required to mark five feature points (two inner eye corners, two mouth corners, and the nose top) on each view. After that, the system is completely automatic. Once the process finishes, his or her constructed face model is displayed and animated. The authors used a feature-based approach to find correspondences. It consists of three steps: (1) detecting corners in each image; (2) matching corners between the two images; (3) detecting false matches based on a robust estimation technique. The reader is referred to Liu et al. [34] for details. Compared to the optical flow approach, the feature-based approach is more robust to intensity and color variations.
After the matching is done, they used both the corner points from the image matching and the five feature points clicked by the user to estimate the camera motion. Because of the matching errors for the corner points and the inaccuracy of the user-clicked points, it is not robust to directly use these points for motion estimation. Therefore they used the physical properties of the user-clicked feature points to improve the robustness. They used the face symmetry property to reduce the number of unknowns and put reasonable bounds on the physical quantities (such as the height of the nose). In this way, the algorithm becomes significantly more robust. The algorithm’s details were described by Liu and Zhang [32].
For the model fitting, they used a linear class of face geometries as their model space. A face was represented as a linear combination of a neutral face (Fig. 20.1) and some number of face metrics, where a metric is a vector that linearly deforms a face in certain way, such as to make the head wider, the nose bigger, and so on.
Fig. 20.1 Neutral face
To be more precise, let us denote the face geometry by a vector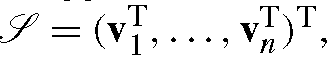
where
are the vertices, and a metric by a vector
Given a neutral face
and a set of m metrics,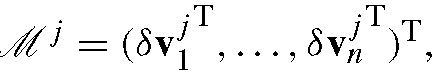
the linear space of face geometries spanned by these metrics is
where cj represents the metric coefficients, and lj and uj are the valid range of cj.
The model fitting algorithm is similar to the approach by Fua and Miccio [13, 14], described earlier in this section. The advantage of using a linear class of face geometries is that it is guaranteed that every face in the space is a reasonable face, and, furthermore, it has fine-grain control because some metrics are global whereas others are only local. Even with a small number of 3D corner points that are noisy, it is still able to generate a reasonable face model. Figure 20.2 shows side-by-side comparisons of the original images with the reconstructed models for various people.
Note that in both approaches just described the model fitting is separated from the motion estimation. In other words, the resulting face model is not used to improve the motion estimation.
During motion estimation, the algorithm by Liu et al. [34] used only general physical properties about human faces. Even though Fua and Miccio [13, 14] used face model during motion estimation, they used it only as a regularizer constraint. The 3D model obtained with their model-driven bundle adjustment is in general inaccurate, and they have to throw away the model and use an additional step to recompute the 3D structure. The problem is that the camera motions are fixed on the second step. It may happen that the camera motions are not accurate owing to the inaccurate model at the first stage, so the structure computed at the second stage may not be optimal either. What one needs is to optimize camera motion and structure together.
Fig. 20.2 Side by side comparison of the original images with the reconstructed models of various people
Shan et al. [49] proposed an algorithm, called model-based bundle adjustment, that combines the motion estimation and model fitting into a single formulation. Their main idea was to directly use the model space as a search space. The model parameters (metric coefficients) become the unknowns in their bundle adjustment formulation. The variables for the 3D positions of the feature points, which are unknowns in the traditional bundle adjustment, are eliminated. Because the number of model parameters is in general much smaller than the isolated points, it results in a smaller search space and better posed optimization system.
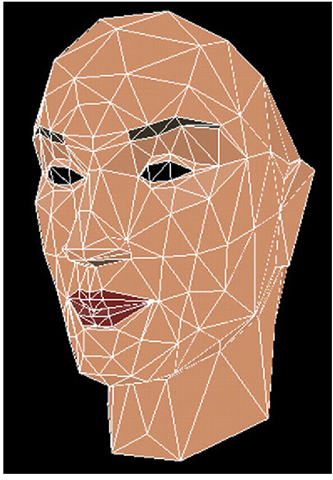
Fig. 20.3 Face mesh comparison. Left: traditional bundle adjustment; Middle: ground truth; Right: model-based bundle adjustment.
Figure 20.3 shows the comparisons of the model-based bundle adjustment with the traditional bundle adjustment. On the top are the front views, and on the bottom are the side views. On each row, the one in the middle is the ground truth, on the left is the result from the traditional bundle adjustment, and on the right is the result from the model-based bundle adjustment. By looking closely, we can see that the result of the model-based bundle adjustment is much closer to the ground truth mesh. For example, on the bottom row, the nose on the left mesh (traditional bundle adjustment) is much taller than the nose in the middle (ground truth). The nose on the right mesh (model-based bundle adjustment) is similar to the one in the middle.
Face Modeling from Two Orthogonal Views
A number of researchers have proposed that we create face models from two orthogonal views [1, 8, 20]: one frontal view and one side view. The frontal view provides the information relative to the horizontal and vertical axis, and the side view provides depth information. The user needs to manually mark a number of feature points on both images. The feature points are typically the points around the face features, including eyebrows, eyes, nose, and mouth. Because of occlusions, the number of feature points on the two views are in general different. The quality of the face model depends on the number of feature points the user provides. The more feature points, the better the model, but one needs to balance between the amount of manual work required from the user and the quality of the model.
Because the algorithm is so simple to implement and there is no robustness issue, this approach has been used in some commercially available systems [19]. Some systems provide a semiautomatic interface for marking the feature points to reduce the amount of the manual work. The disadvantage is that it is not convenient to obtain two orthogonal views, and it requires quite a number of manual interventions even with the semiautomatic interfaces.
Face Modeling from a Single Image
Blanz and Vetter [5] developed a system to create 3D face models from a single image. They used both a database of face geometries and a database of face textures. The geometry space is the linear combination of the example faces in the geometry database. The texture space is the linear combination of the example texture images in the image database. Given a face image, they search for the coefficients of the geometry space and the coefficients of the texture space so the synthesized image matches the input image. More details can be found in Chap. 10 and in their paper [5]. One limitation of their current system is that it can only handle the faces whose skin types are similar to the examples in the database. One could potentially expand the image database to cover more varieties of skin types, but there would be more parameters and it is not clear how it is going to affect the robustness of the system.
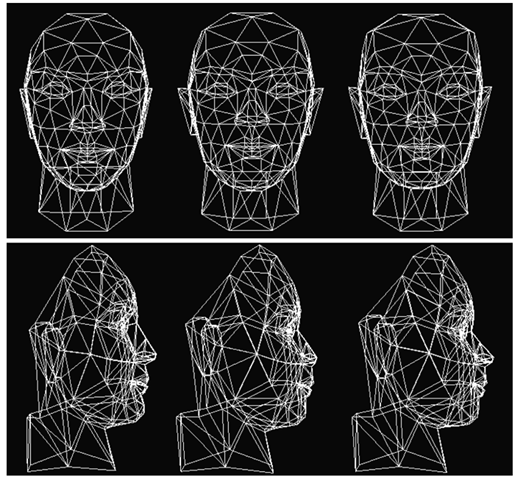
Liu [31] developed a fully automatic system to construct 3D face models from a single frontal image. They first used a face detection algorithm to find a face and then a feature alignment algorithm to find face features. By assuming an orthogonal projection, they fit a 3D face model by using the linear space of face geometries described in Sect. 20.2.1. Given that there are existing face detection and feature alignment systems [28, 62], implementing this system is simple. The main drawback of this system is that the depth of the reconstructed model is in general not accurate. For small head rotations, however, the model is recognizable. Figure 20.4 shows an example where the left is the input image and the right is the feature alignment result. Figure 20.5 shows the different views of the reconstructed 3D model. Figure 20.6 shows the results of making expressions for the reconstructed face model.
Fig. 20.4 Left: input image. Right: the result from image alignment.
Fig. 20.5 Views of the 3D model generated from the input image in Fig. 20.4.
Fig. 20.6 Generating different expressions for the constructed face model.
Face Relighting
During the past several years, a lot of progress has been made on generating photo-realistic images of human faces under arbitrary lighting conditions [21, 26, 50, 53, 57, 64]. One class of method is inverse rendering [9, 10, 15, 36, 38, 63]. By capturing the lighting environment and recovering surface reflectance properties, one can generate photo-realistic rendering of objects including human faces under new lighting conditions. To recover the surface reflectance properties, one typically needs special setting and capturing equipment. Such systems are best suited for studio-like applications.
Face Relighting Using Ratio Images
Riklin-Raviv and Shashua [46] proposed a ratio-image technique to map one person’s lighting condition to a different person. Given a face under two different lighting conditions, and another face under the first lighting condition, they used the color ratio (called the quotient image) to generate an image of the second face under the second lighting condition. For any given point on the face, let ρ denote its albedo, and n its normal. Let
be the irradiances under the two lighting conditions, respectively. Assuming a Lambertian reflectance model, the intensities of this point under the two lighting conditions are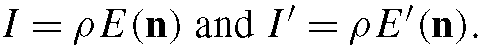
Given a different face, let pi be its albedo. Then its intensities on the two lighting conditions are
Therefore, we have
Thus,
Equation (20.4) shows that one can obtain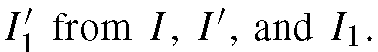
If we have one
person’s images under all possible lighting conditions and the second person’s image under one of the lighting conditions, we can use (20.4) to generate the second person’s images under all the other lighting conditions.
In many applications, we do not know in which lighting condition the second person’s image is. Riklin-Raviv and Shashua [46] proposed that we use a database of images of different people under different lighting conditions. For any new person, if its albedo is “covered by” (formally called “rational span”, see Riklin-Raviv and Shashua [46] for details) the albedos of the people in the database, it is possible to figure out in which lighting condition the new image was.
Face Relighting from a Single Image
Researchers have developed face relighting techniques that do not require a database [21, 57, 59, 64]. Given a single image of a face, Wen et al. [59] first computed a special radiance environment map assuming known face geometry. For any point on the radiance environment map, its intensity is the irradiance at the normal direction multiplied by the average albedo of the face. In other words, the special radiance environment map is the irradiance map times a constant albedo. Zhang and Samaras [64] and Jiang et al. [21] proposed statistical approaches to recover the spherical harmonic basis images from the input image. A bootstrap step is required to obtain the statistical texture and shape information of human faces. To estimate the lighting, shape and albedo of a human face simultaneously from a single image, Wang et al. [57] used the 3D spherical harmonic morphable model (SHBMM), an integration of spherical harmonics into the morphable model framework. Thus, any face under arbitrary pose and illumination conditions can be represented simply by three low dimensional vectors: shape parameters, spherical harmonic basis parameters, and illumination coefficients. In this section, we describe the technique proposed by Wen et al. [59] in more detail.
Given a single image of a face, Wen et al. [59] computed the special radiance environment map using spherical harmonic basis functions [3, 45] . Accordingly, the irradiance can be approximated as a linear combination of nine spherical harmonic basis functions [3, 45].
Wen et al. [59] also expanded the albedo function p(n) using spherical harmonics
where ρ00 is the constant component, and
contains other higher order components.
From (20.5) and (20.6), we have
If we assume
does not have first four order (l = 1, 2, 3,4) components, the second term of the righthand side in (20.7) contains components with orders equal to or higher than 3 (see Wen et al. [59] for the explanation). Because of the orthogonality of the spherical harmonic basis, the nine coefficients of order
estimated from
with a linear least-squares procedure a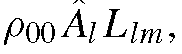re
where
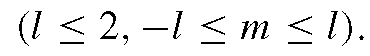Therefore, we obtain the radiance environment map with a reflectance coefficient equal to the average albedo of the surface.
Wen et al. [59] argued that human face skin approximately satisfies the above assumption, that is, it does not contain low frequency components other than the constant term.
Fig. 20.7 Comparison of synthesized results and ground truth. The top row is the ground truth. The bottom row is the synthesized result, where the middle image is the input.
By using a generic 3D face geometry, Wen et al. [59] set up the following system of equations:
They used a linear least-squares procedure to solve the nine unknowns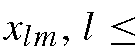
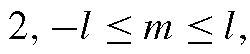thus obtaining the special radiance environment map.
One interesting application is that one can relight the face image when the environment rotates. For the purpose of explanation, let us imagine the face rotates while the environment is static. Given a point on the face, its intensity is 
The intensity of the corresponding point on the radiance environment map is
where p is the average albedo of the face. After rotation, denote n’ to be the new normal. The new intensity on the face is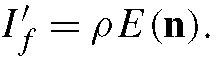
The intensity on the radiance environment map corresponding to the
Therefore,
The bottom row of Fig. 20.7 shows the relighting results. The input image is the one in the middle. The images at the top are the ground truth. We can see that the synthesized results match well with the ground truth images. There are some small differences mainly on the first and last images due to specular reflections. (According to Marschner et al. [37], human skin is almost Lambertian at small light incidence angles and has strong non-Lambertian scattering at higher angles.)
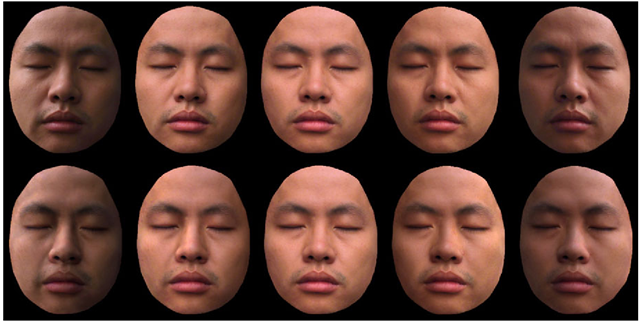
Another application is that one can modify the estimated spherical harmonic coefficients to generate radiance environment maps under the modified lighting con-ditions. For each new radiance environment map, one can use the ratio-image technique (see (20.8)) to generate the face image under the new lighting condition. In this way, one can modify the lighting conditions of the face. In addition to lighting editing, this can also be used to generate training data with different lighting conditions for face detection or face recognition applications.
Fig. 20.8 Lighting editing by modifying the spherical harmonics coefficients of the radiance environment map. The left image in each pair is the input image and the right image is the result after modifying the lighting.
Figure 20.8 shows four examples of lighting editing by modifying the spherical harmonics coefficients. For each example, the left image is the input image, and the right image is the result after modifying the lighting. In example (a), lighting is changed to attach shadow to the person’s left face. In example (b), the light on the person’s right face is changed to be more reddish, and the light on her left face becomes slightly more bluish. In (c), the bright sunlight move from the person’s left face to his right face. In (d), we attach shadow to the person’s right face and change the light color as well.
