Related Works
In addition to the general mean criteria and max-min distance analysis, there are also some methods proposed in recent years to deal with the class separation problem of FLDA. Among these methods, approximate pairwise accuracy criterion (aPAC) [28] and fractional step LDA (FS-LDA) [30] are the most representative ones, and both of them use weighting schemes to emphasize close class pairs during subspace selection. Besides, the Bayes optimality of FLDA is further studied when the dimensionality of subspace is less than class number minus 1. In particular, it is shown that the one dimensional Bayes optimal subspace can be obtained by convex optimization given the information of the order of class centers projected onto the subspace [18]. Such result generalizes the early result of Bayes optimal one dimensional Bayes optimal subspace on a special case of three Gaussian distributions [36]. Further, the authors of [18] suggested selecting a general subspace by greedy one dimensional subspace selection and orthogonal projection. The homoscedastic Gaussian assumption is another limitation of FLDA. Various methods have been developed to extend FLDA to heteroscedastic Gaussian cases, e.g., the using of information theoretic divergences such as Kullback-Leibler divergence [10, 39], and Chernoff [29] or Bhattacharyya distance [35] to measures the discrimination among heteroscedastic Gaussian distributions. Besides, nonparametric and semiparametric method provide alternative ways for extensions of FLDA, by which classic work includes Fukunaga’s nonparametric discriminant analysis (NDA) [16], its latest extension to multiclass case [27] and subclass discriminant analysis [57]. In addition, recent studies show that FLDA can be converted to a least square problem via a proper coding of class labels [49, 50]. The advantages of such least square formulation are that the computational speed can be significantly improved and also regularizations on the subspace are more readily imposed.
Subspace Learning—A Local Perspective
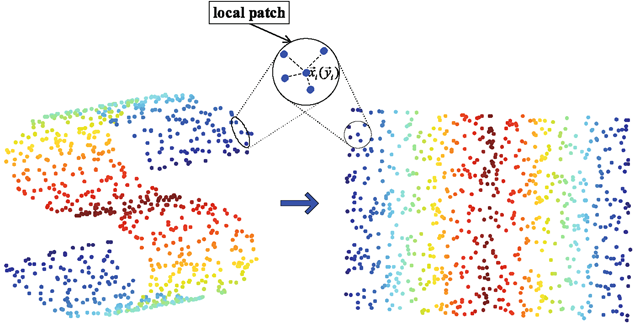
It has shown that the global linearity of PCA and FLDA prohibit their effectiveness for non-Gaussian distributed data, such as face images. By considering the local geometry information, a dozen of manifold learning algorithms have been developed, such as locally linear embedding (LLE) [34], ISOMAP [40], Laplacian eigen-maps (LE) [2], Hessian eigenmaps (HLLE) [11], and local tangent space alignment (LTSA) [53]. All of these algorithms have been developed intuitively and pragmatically, that is, on the base of the experience and knowledge of experts for their own purposes. Therefore, it will be more informative to provide some a systematic framework for understanding the common properties and intrinsic differences in the algorithms. In this section, we introduce such a framework, that is, “patch alignment”, which consists of two stages: part optimization and whole alignment. The framework reveals (i) that algorithms are intrinsically different in the patch optimization stage and (ii) that all algorithms share an almost identical whole alignment stage.
Patch Alignment Framework
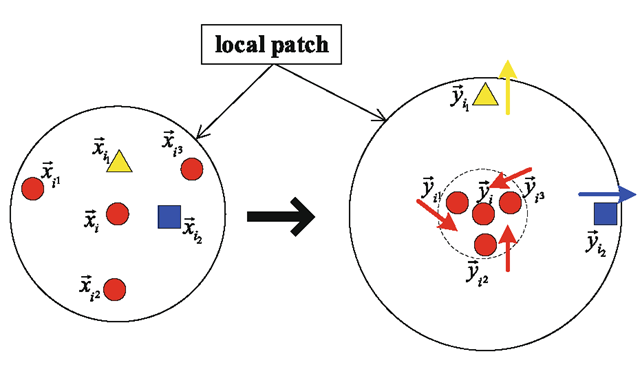
The patch alignment framework [55] is composed of two ingredients, first, part optimization and then whole alignment. For part optimization, different algorithms have different optimization criteria over patches, each of which is built by one measurement associated with its related ones. For whole alignment, all part optimizations are integrated into together to form the final global coordinate for all independent patches based on the alignment trick. Figure 3.4 illustrates the patch alignment framework.
Given an instance Xi and its k nearest neighbors![tmpdece-198_thumb[2] tmpdece-198_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece198_thumb2_thumb.png) the part optimization at Xi is defined by
the part optimization at Xi is defined by
Fig. 3.4 Patch alignment framework
where![tmpdece-202_thumb[2] tmpdece-202_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece202_thumb2_thumb.png) is projection of the local patch
is projection of the local patch![tmpdece-203_thumb[2] tmpdece-203_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece203_thumb2_thumb.png)
![tmpdece-204_thumb[2] tmpdece-204_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece204_thumb2_thumb.png) onto the low dimensional subspace, and Li encodes the local geometry information at instance Xi and is chosen algorithm-specifically. By summarizing part optimizations over all instances, we get
onto the low dimensional subspace, and Li encodes the local geometry information at instance Xi and is chosen algorithm-specifically. By summarizing part optimizations over all instances, we get
Let![tmpdece-209_thumb[2] tmpdece-209_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece209_thumb2_thumb.png) be the projection of all instances
be the projection of all instances![tmpdece-210_thumb[2] tmpdece-210_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece210_thumb2_thumb.png) As for each local patch Yi should be a subset of the whole alignment Y, the relationship between them can be expressed by
As for each local patch Yi should be a subset of the whole alignment Y, the relationship between them can be expressed by
where Si is a proper 0-1 matrix called the selection matrix. Thus,
with
called the alignment matrix. Further by letting Y = UtX, that is, a linear projection, (3.18) is rewritten as
Table 3.1 Manifold learning algorithms filled in the patch alignment framework
Further, we can impose the orthogonal constraint UtU = I on the projection matrix U, or the constraint Y tY = I on the Y, which leads to U tXXtU = I .In both cases, (3.20) is solved by eigen- or generalized eigen-decomposition.
Among all the manifold learning algorithms, the most representatives are locally linear embedding (LLE) [34], ISOMAP [40], Laplacian eigenmaps (LE) [2]. LLE uses linear coefficients to represent local geometry information, and find a lowdimensional embedding such that these coefficients are still suitable for reconstruction. ISOMAP preserves geodesic distances between all instance pairs. And LE preserves proximity relationships by manipulations on an undirected weighted graph, which indicates neighbor relations of pairwise instances. It has been shown that all these algorithms can be filled into the patch alignment framework, where the difference among algorithms lies in the part optimization stage while the whole alignment stage is almost the same. There are also other manifold learning algorithms, for example, Hessian eigenmaps (HLLE) [11], Generative Topographic Mapping (GTM) [6] and local tangent space alignment (LTSA) [53]. We can use the patch alignment framework to explain them in a unified way. Table 3.1 summarizes these algorithms in the patch alignment framework.
Fig. 3.5 The motivation of DLA. The measurements with the same shape and color come from the same class
Discriminative Locality Alignment
One representative subspace selection method based on the patch alignment framework is the discriminative locality alignment (DLA) [54]. In DLA, the discriminative information, encoded in labels of samples, is imposed on the part optimization stage and then the whole alignment stage constructs the global coordinate in the projected low-dimensional subspace.
Given instance Xi and its k nearest neighbors![tmpdece-223_thumb[2] tmpdece-223_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece223_thumb2_thumb.png) we divide the k neighbors into two groups according to the label information, that is, belonging to the same class with Xi or not. Without losing generality, we can assume the first k1 neighbors
we divide the k neighbors into two groups according to the label information, that is, belonging to the same class with Xi or not. Without losing generality, we can assume the first k1 neighbors![tmpdece-224_thumb[2] tmpdece-224_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece224_thumb2_thumb.png) having the same class label with Xi and the rest k —
having the same class label with Xi and the rest k —
k1 neighbors![tmpdece-225_thumb[2] tmpdece-225_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece225_thumb2_thumb.png) having different class labels (otherwise, we just have to resort the indexes properly). And their low dimensional representations are
having different class labels (otherwise, we just have to resort the indexes properly). And their low dimensional representations are![]() respectively. The key idea of DLA is enforcing
respectively. The key idea of DLA is enforcing![tmpdece-227_thumb[2] tmpdece-227_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece227_thumb2_thumb.png) while pushing it apart
while pushing it apart
from![tmpdece-228_thumb[2] tmpdece-228_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece228_thumb2_thumb.png) Figure 3.5 illustrates such motivation.
Figure 3.5 illustrates such motivation.
For instance, Xi and its same class neighbors, we expect the summation of squared distance in the low dimensional subspace to be as small as possible, that is,
However, for Xi and its different class neighbors, we want the corresponding result to be large, that is,
A convenient tradeoff between (3.21) and (3.22) is
where γ is a scaling factor between 0 and 1 to balance the importance between measures of the within-class distance and the between-class distance. Let
then (3.23) is readily rewritten as
where
To obtain the projection mapping y = UTx, we just substitute (3.26) into the whole alignment formula (3.18), and solve the eigen-decomposition problem with constraint UtU = I. It is worth emphasizing some merits of DLA here: (1) it exploits local geometry information of data distribution; (2) it is ready to deal with the case of nonlinear boundaries for class separation; (3) it avoids the matrix singularity problem.
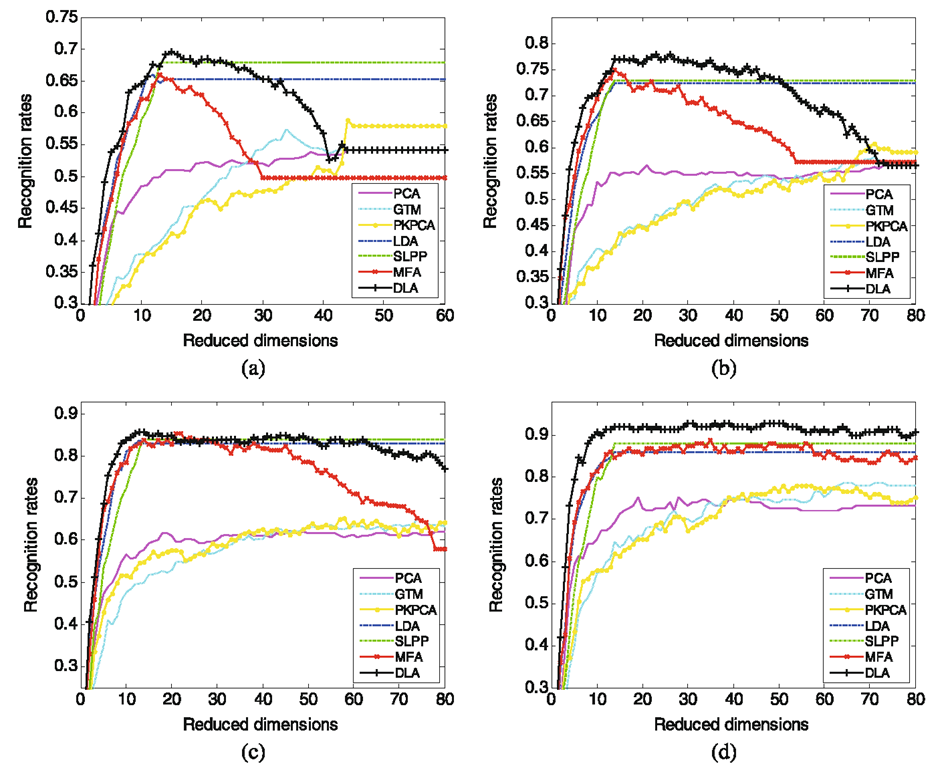
Now we evaluate the performance of the proposed DLA in comparison with six representative algorithms, that is, PCA [23], Generative Topographic Mapping (GTM) [6], Probabilistic Kernel Principal Components Analysis (PKPCA) [42], LDA [14], SLPP [7] and MFA [48], on Yale face image dataset [1]. For training, we randomly selected different numbers (3, 5, 7, 9) of images per individual, used 1 /2 of the rest images for validation, and 1 /2 of the rest images for testing. Such trial was independently performed ten times, and then the average recognition results were calculated. Figure 3.6 shows the average recognition rates versus subspace dimensions on the validation sets, which help to select the best subspace dimension. It can be seen that DLA outperforms the other algorithms.
Manifold Elastic Net
Manifold elastic net (MEN) [56] is a subspace learning method built upon the patch alignment framework. However, the key feature of MEN is that it is able to achieve sparse basis (projection matrix) by imposing the popular elastic net penalty (i.e., the combination of the lasso penalty and the L2 norm penalty). As sparse basis are more interpretable both psychologically and physiologically, MEN is expected to give more meaningful results on face recognition, which will be shown in experiments later.
First, MEN uses the same part optimization and whole alignment as in DLA, that is, the following minimization is considered
Fig. 3.6 Recognition rate vs. subspace dimension on Yale dataset. a 3 images per subject for training; b 5 images per subject for training; c 7 images per subject for training; d 9 images per subject for training
However, rather than substituting Y = UtX directly, (3.27) is reformed equivalently as below
Note that (3.28) indeed will lead to Y = UTX. Given the equivalence between the two formulations, the latter is more convenient to incorporate the minimization of classification error. Specifically, letting stores the response or prediction result, which are proper encodings of the class label information, we expect UtX to be close to T, that is,
By combing (3.28) and (3.29), we get the main objective of MEN
where a and β are trade-off parameters to control the impacts of different terms.
To obtain a sparse projection matrix U, an ideal approach is to restrict the number of nonzero entries in it, that is, using the L0 norm as a penalty over (3.30). However, the L0 norm penalized (3.30) is an NP-hard problem and thus intractable practically. One attractive way of approximating the L0 norm is the L1 norm, i.e., the Lasso penalty [41], which is convex and actually the closet convex relaxation of the L0 norm. Various efficient algorithms exist for solving Lasso penalized least square regression problem, including the LARS [13]. However, the lasso penalty has the following two disadvantages: (1) the number of variables to be selected is limited by the number of observations and (2) the lasso penalized model can only selects one variable from a group of correlated ones and does not care which one should be selected. These limitations of Lasso are well addressed by the so-called elastic net penalty, which combines the L2 and L1 norm together. MEN adopts the elastic net penalty [58]. In detail, the L2 of the projection matrix is helpful to increase the dimension (and the rank) of the combination of the data matrix and the response. In addition, the combination of the Li and L2 of the projection matrix is convex with respect to the projection matrix and thus the obtained projection matrix has the grouping effect property. The final form of MEN is given by
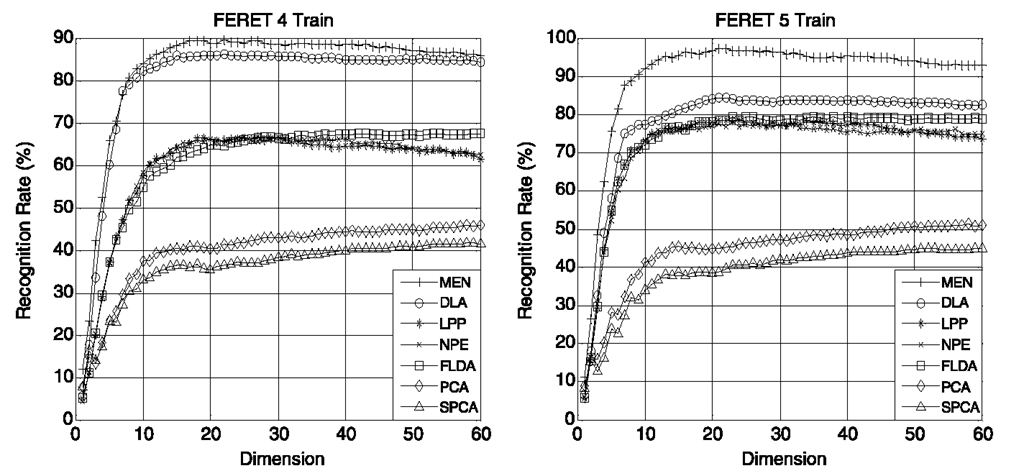
We report an empirical evaluation of MEN on the FERET dataset. From in total 13 539 face images of 1565 individuals, 100 individuals with 7 images per subject are randomly selected in the experiment. 4 or 5 images per individual are selected as training set, and the remaining is used for test. All experiments are repeated five times, and the average recognition rates are calculated. Six representative dimension reduction algorithms, that is, principal component analysis (PCA) [23], Fisher’s linear discriminant analysis (FLDA) [14], discriminative locality alignment (DLA) [54], supervised locality preserving projection (SLPP) [7], neighborhood preserving embedding (NPE) [19], and sparse principal component analysis (SPCA) [9], are also performed for performance comparison.
The performance of recognition is summarized in Fig. 3.7. Apparently, the seven algorithms are divided into 3 groups according to their performance. The baseline level methods are PCA and SPCA, which is because they are both unsupervised methods and thus may not give satisfying performance due to the missing of label information. LPP, NPE and LDA only show moderate performance. In contrast, DLA and MEN give rise to significant improvements. Further, the sparsity of MEN makes it outperform DLA. The best performance of MEN is actually not surprising, since it considers the most aspects on data representation and distribution, including the sparse property, the local geometry information and classification error minimization.
Figure 3.8 shows the first ten bases selected by different subspace selection methods. One can see that the bases selected by LPP, NPE and FLDA are contaminated by considerable noises, which explains why they only give moderate recognition performance.
Fig. 3.7 Performance evaluation on the FERET dataset
Fig. 3.8 Plots of first 10 bases obtained from 7 dimensionality reduction algorithms on FERET for each column, from top to bottom: MEN, DLA, LPP, NPE, FLDA, PCA, and SPCA
The bases from PCA, that is, Eigenfaces, are smooth but present relatively few discriminative information. In terms of sparsity, SPCA gives the desired bases; however, the problem is that the patterns presented in these bases are not grouped so that cannot provide meaningful interpretation. The bases from MEN, which we call “MEN’s faces”, have a low level of noise and are also reasonably sparse. And more importantly, thanks to the elastic net penalty, the sparse patterns of MEN’s bases are satisfying grouped, which gives meaningful interpretations, for example, most discriminative facial features are obtained, including eyebrows, eyes, nose, mouth, ears and facial contours.
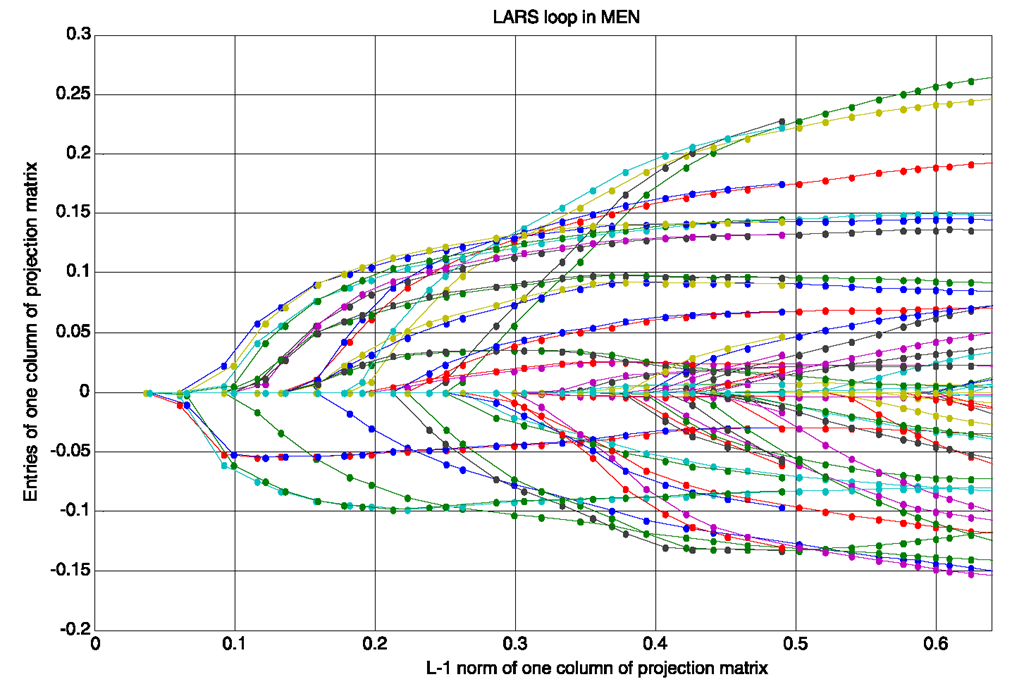
Fig. 3.9 Entries of one column of projection matrix vs. its L1 norm in one LARS loop of MEN
The optimization algorithm of MEN is built upon LARS. In each LARS loop of the MEN algorithm, all entries of one column in the projection matrix are zeros initially. They are sequentially added into the active set according to their importance. The values of active ones are increased with equal altering correlation. In this process, the L1 norm of the column vector is augmented gradually. Figure 3.9 shows the altering tracks of some entries of the column vector in one LARS loop. These tracks are called “coefficient paths” in LARS. As shown by these plots, one can observe that every coefficient path starts from zero when the corresponding variable becomes active, and then changes its direction when another variable is added into the active set. All the paths keep in the directions which make the correlations of their corresponding variables equally altering. The L1 norm is increasing along the greedy augment of entries. The coefficient paths proceed along the gradient decent direction of objective function on the subspace, which is spanned by the active variables.
In addition, Fig. 3.10 shows 10 of the 1600 coefficient paths from LAPS loop. It can be seen that MEN selects ten important features sequentially. For each feature, its corresponding coefficient path and the “MEN face” when the feature is added into active set are assigned the same color which is different with the other 9 features. In each “MEN face”, the new added active feature is marked by a small circle, and all the active features are marked by white crosses. The features selected by MEN can produce explicit interpretation of the relationship between facial features and face recognition: feature 1 is the left ear, feature 2 is the top of nose, feature 3 is on the head contour, feature 4 is the mouth, feature 5 and feature 6 are on the left eye, feature 7 is the right ear, and feature 8 is the left corner of mouth. These features are already verified of great importance in face recognition by many other famous face recognition methods. Moreover, Fig. 3.10 also shows MEN can group correlated features, for example, feature 5 and feature 6 are selected sequentially because they are both on the left eye. In addition, features which are not very important, such as feature 9 and feature 10 in Fig. 3.10, are selected after the selection of the other more significant features and assigned smaller value than those more important ones. Therefore, MEN is a powerful algorithm in feature selection.
Fig. 3.10 Coefficient paths of 10 features in one column vector
![tmpdece-200_thumb[2] tmpdece-200_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece200_thumb2_thumb.png)
![tmpdece-208_thumb[2] tmpdece-208_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece208_thumb2_thumb.png)
![tmpdece-213_thumb[2] tmpdece-213_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece213_thumb2_thumb.png)
![tmpdece-214_thumb[2] tmpdece-214_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece214_thumb2_thumb.png)
![tmpdece-215_thumb[2] tmpdece-215_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece215_thumb2_thumb.png)
![tmpdece-221_thumb[2] tmpdece-221_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece221_thumb2_thumb.png)
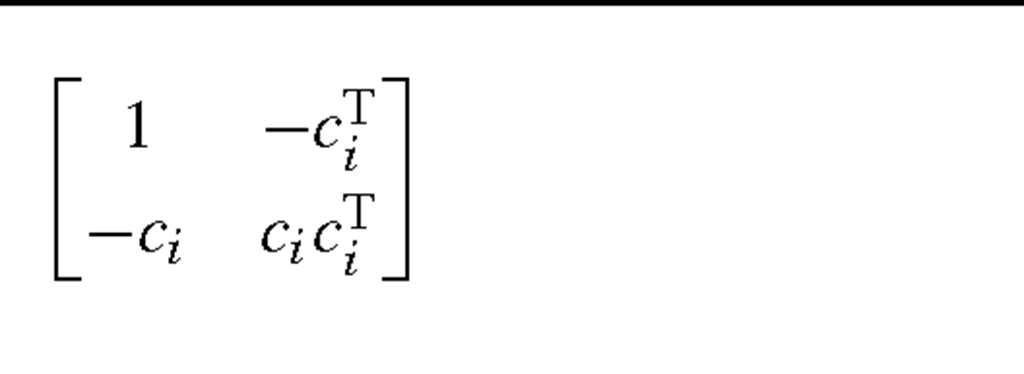
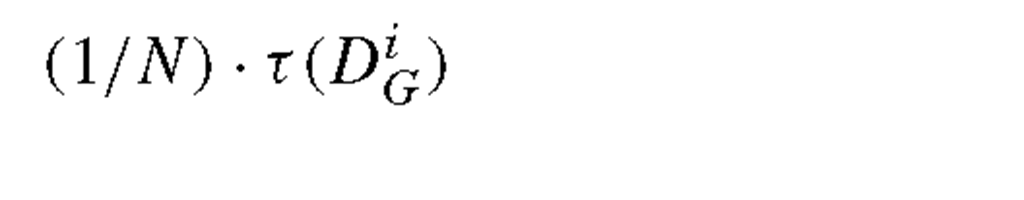
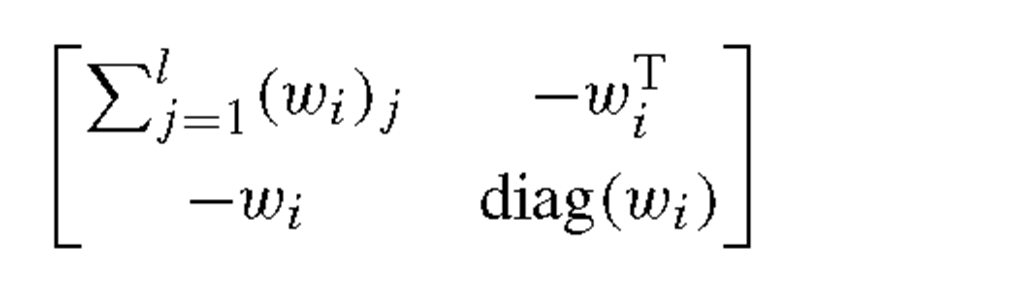
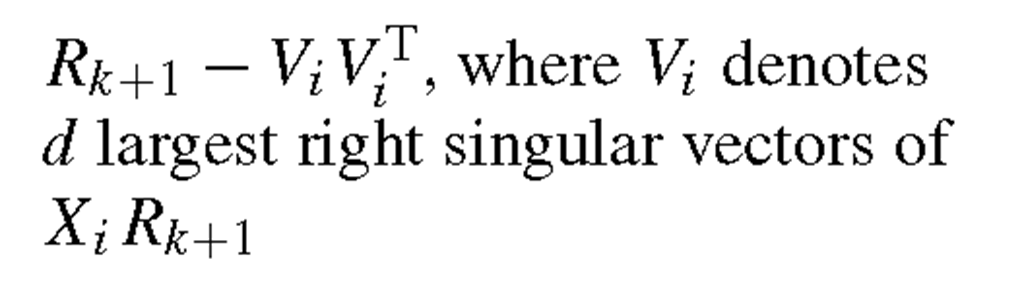

![tmpdece-235_thumb[2] tmpdece-235_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece235_thumb2_thumb.png)
![tmpdece-236_thumb[2] tmpdece-236_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece236_thumb2_thumb.png)
![tmpdece-237_thumb[2] tmpdece-237_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece237_thumb2_thumb.png)
![tmpdece-238_thumb[2] tmpdece-238_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece238_thumb2_thumb.png)
![tmpdece-239_thumb[2] tmpdece-239_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece239_thumb2_thumb.png)
![tmpdece-240_thumb[2] tmpdece-240_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece240_thumb2_thumb.png)
![tmpdece-241_thumb[2] tmpdece-241_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece241_thumb2_thumb.png)
![tmpdece-243_thumb[2] tmpdece-243_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece243_thumb2_thumb.png)
![tmpdece-244_thumb[2] tmpdece-244_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece244_thumb2_thumb.png)
![tmpdece-245_thumb[2] tmpdece-245_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece245_thumb2_thumb.png)
![tmpdece-246_thumb[2] tmpdece-246_thumb[2]](http://what-when-how.com/wp-content/uploads/2012/06/tmpdece246_thumb2_thumb.png)