Damage Analysis of the Ceramic Reinforced Steel Matrix Composites Sheets: Experimental and Numerical Study (Experimental and Applied Mechanics) Part 2

Results

The FE solution used to simulate two-phase composites consisting of an elasto-plastic matrix reinforced by linear elastic inclusions. The predictions of the mean-field models are compared to the reference results from FE computations on representative cells containing a random arrangement of multiple inclusions. Uniaxial compressive loading are successively applied to the multi particle cells embedded in the metal iron matrix. The average of the macroscopic strain computed at each time step provides the loading history for the corresponding FE models.

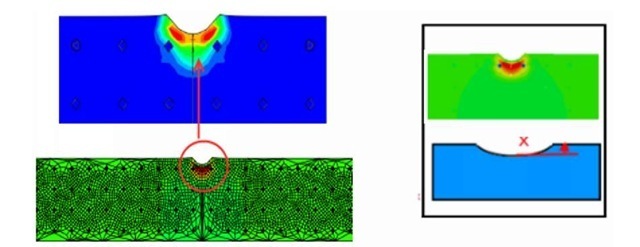
Average equivalent stress in the inclusions of two phase MMC material is determined for 2 volume fractions of the reinforcing phase 10 % and 20%. For comparison, the predictions of the compressive results, by mean of deformation and maximum loading are shown for uniaxial compression Figures 8, 9 and Table 1. The average volume fraction for specimens in Table 1 is taken to be 15 %. Only the results due to compressive tests using a rigid sphere are presented here.

Fig. 8. FEM measurements of the deformation depth under compression of the MMC under compressive tests (Equivalent plastic strain distributions in the contact area)

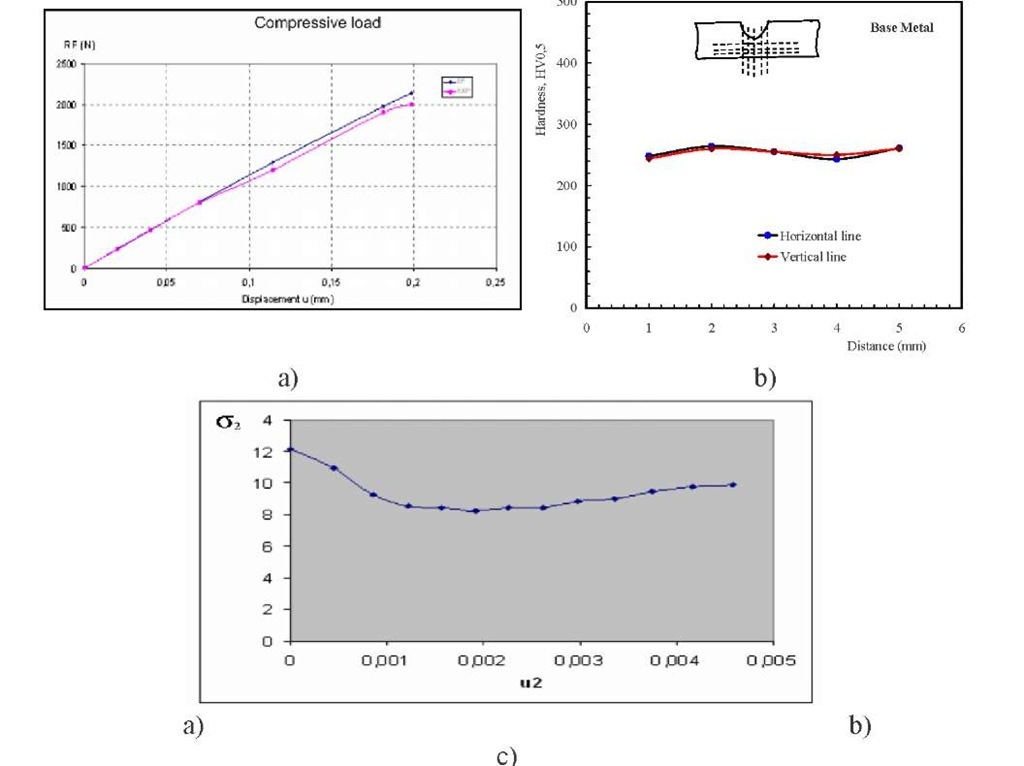
In fact, Figure 9 gives comprehensive evaluation of the deformation behaviour of this material as noted form experimental and FEM variation of the compressive load as a function of displacement under compressive tests. However, interesting results have been obtained from hardness measurements carried out in vertical and horizontal direction under the deformed area due to compression test (experimental) and also very similar results were obtained from variation of the stress c2 as a function of displacement due to compression test (FEM). These results show clearly that a strain hardening mechanism does not occur in this material what ever the deformation level (from small stress levels up to stresses induced failure);

First of all, the structure of the matrix is similar that of the pure iron. It contains very low carbon and the microstructure contains very low dislocation density that does not increase during the deformation even if the microstructure with small grain size. Most probably, the hardness values around the deformed area and also variation of the stress c2 as a function of displacement do not change during the deformation and the materials does not show a noticed work hardening phenomenon.

Fig. 9. a) Experimental and FEM variation of the compressive load as a function of displacement of the MMC under compressive tests and b)Hardness evolution in different direction after compression test (experimental) and c) FEM variation of the stress c2 as a function of displacement of the MMC under compressive tests

Partial Discussion of FE results

The inclusions response is predicted based on the solution of inclusions in a finite medium having the properties of the matrix. This equivalent inclusion problem is solved by the FE method, allowing field heterogeneities to take place in the made up matrix. In this model the scheme of Mori-Tanaka model is used, the average of the strain in the actual matrix of the composite is taken as far-field strain. The new method is applied to this composite made of an elasto-plastic iron matrix reinforced by spherical or cylindrical elastic TiB2 inclusions. Macroscopic deformation histories corresponding to non-monotonic uniaxial and plane strain tension/compression are successively considered. In all cases, predictions of the approaches are compared to reference results obtained by FE simulations on cells containing inclusions.

This FE study showed that the M-T assumption is able to simulate the effective response of such composites almost for less then 20% of inclusion volume fraction. However, the predicted inclusion response is, in general, less accurate than the macroscopic real one so that the stress level in low inclusion fraction is underestimated by the mean-field model, this fact was well discussed in a number of previous works [15-17]. This effect is due to a certain extent, compensated by the matrix prediction which raises the stress level in the effective response. This is due to a slight overestimation of the matrix average strain combined with the present comparison material for the matrix. For higher volume fractions (from 20 %) the single inclusion modelling yields very poor predictions of the inclusion response. This can be explained by plastic localization taking place between inclusions in the real composite, which is overlooked by the FE model (Figure 9).

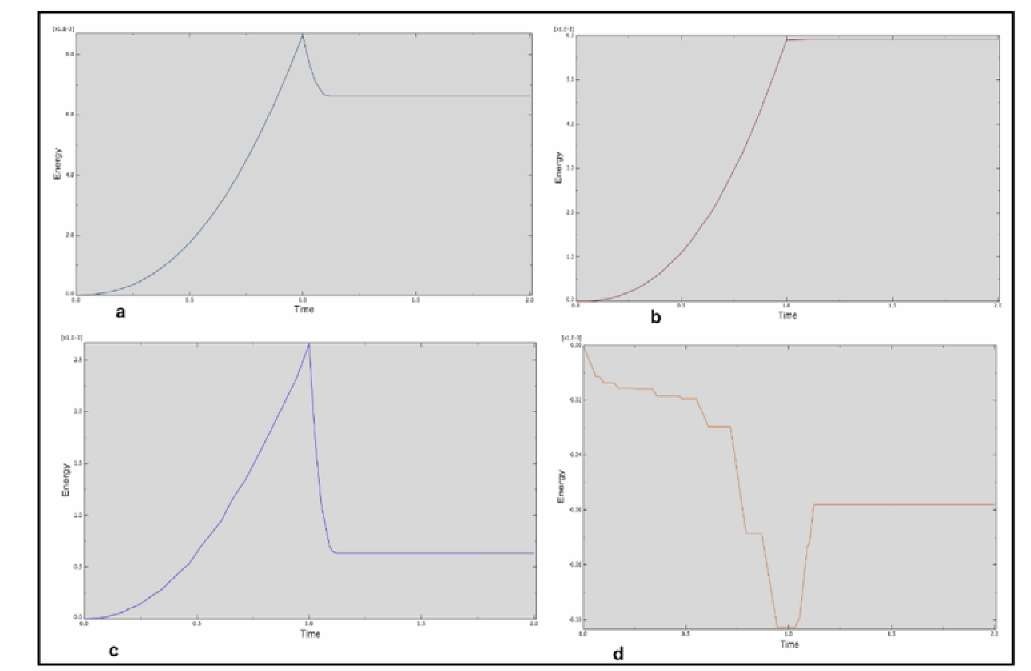
Figure 10 illustrates the history of energy for the same plate, both total energy and strain energy figure 17 a and c show the same shape at the loading step, then the energy falls to low values and this sharp drop can join the experimental results obtained with Charpy choc test as the energy transition was dropped sharply from the ductile to the brittle zone. This sudden jump is due to the repartition and the size of the TiB2 particles. Development of a new iron matrix, composite reinforced with TiB2, needs more investigations to attempt a high accuracy between experimental results and their equivalent FE predictions. The best choice of the volume fraction and the size particle is a competitive compromise that could be defined accordingly to the industrial destination of the MMC material. In fact, a larger investigation in the development of these materials can lead to the development of a smart strategy that can be easily used in the future to design smart MMC materials that can be adapted to the functionality of this latter. So that the material composition and the geometry design of the phase distribution in the MMC matrix could be monitored from an application to other.

Fig. 10. FEM variation of the stress energy history of the MMC under compressive tests

Table1. General evaluation to compare experimental and FE results form compression test

General Conclusion

Some of the conclusions can be driven from partial results of this study;

- TiB2 particulate reinforced MMCs sheets were successfully manufactured as proposed in the Patent.

- Weldability of this new steel family has a big potential success in manufacturing engineering (Formability of tailored welded blanks, TWBs)

- Weld bead shows finer structure

- There is no abnormal evolution in HAZ during the welding (e.g. grain growth) -The weld bead shows a fine eutectic structure.

-There is no abnormal evolution in the HAZ (e.g., grain growth).

- Preliminary work suggests that this product (originally developed for the car industry) should find other applications for all of the structures designed by stiffness (ex: energy domain, road transport and railway)

- A finite element model of the MMC material has been developed using a specimen with specific geometry and material properties. Accurate determination of material parameters is an integral component of developing a Fe -TiB2 MMC. For most direct estimation, parameters would be determined using standard experimental test techniques (e.g. uniaxial tension or compression). For intention of modelling MMC iron composites, preparation of excised samples presents a number of difficulties. If insertion of inclusion particles is not well designed, it could affect the final result of simulation and it can induce false correlation between external and internal variables. Finally, even if uniaxial properties are precisely measured, the applicability of such data, and resulting material parameters, need a robust simulation to reach the satisfactory conclusions about the mechanical behaviour of those materials.

- In general, the development of this MMC material is enhanced for many causes, in particular as far as we are looking for improving some roughness properties, we can associate particular attention to the grain size, because when it is reduced at a large scale, the presence of stresses and imperfections introduced by mechanical alloying enhance the roughness property; the overall roughness property is a competition between decrease in grain size and increase in strain. An enhancement of the numerical model to a nano scale can be with a great utility to bring more light and answers on the mechanical improvement of this material.