ABSTRACT
This paper reports damage analysis of TiB2 (ceramic particles) reinforced steel matrix composite sheets. This new steel composite receives much attention as potential structural materials due to their high specific strength and stiffness. The goal of the research described in this paper is to study the usage of this new steel family in the manufacture of light structures. Therefore, titanium diboride TiB2 reinforced steel matrix composite sheets were characterized by optical and scanning electron microscopes after the mechanical tests carried out on the base metal and welded specimens under dynamic and static test conditions. However, the non homogeneity of the structure in this type of composites makes deeply complexity of their numerical and analytical modelling to predict their damage during the loading. For example, the interfaces essentially play a key role in determining mechanical and physical properties. A Finite Element (FEM) analysis is also used for modelling to simulate the macroscopic behaviour of this material, taking into account the relevant microscopic scales.
Keywords: Steel matrix composites; Ceramic particles-TiB2; Crash test; Welding; Weldability
Introduction
Metal Matrix Composites (MMCs) have recently received considerable attention in manufacturing engineering as potential structural materials due to their high specific strength and stiffness [1-6, 8-12]. While most work on MMCs is directed towards producing novel and lightweight engineering materials, there is also considerable interest in developing iron and steel matrix composites. Iron and steel matrix composites reinforced with TiB2/TiC ceramic particulates have been the focus of intensive investigation due to their ease of fabrication, low costs and isotropic properties. These materials potentially have good wear resistance with an excellent combination of low density and high toughness values [1, 4, 5]. For this reason, MMCs with fresh, ultrafine and stable ceramic reinforcements can demonstrate outstanding mechanical properties [6]. Among various ceramic particulates, titanium carbide (TiC) and titanium diboride (TiB2) are good candidate materials because of their excellent properties such as high hardness, low density, high melting temperature, high modulus, good wear and corrosion resistance [5, 7, 10-12]. These materials are highly attractive for automotive applications, because their lightness and high toughness make them conducive to the production of environmentally friendly cars. However, several limitations associated with the use of pure TiC and TiB2 were found in the literature [5-7, 9-12]. The first theme concerns the microstructural evolution of the composite sheets as base and welded structures due to their potential use in the automotive industry. The second theme is the relationship between microstructural and mechanical properties, notably weldability and the ductile brittle transition temperature of these steel matrix composite (TiB2-RSMCs) sheets recently invented and developed by the ARCELOR Research Group in France [1]. Introducing these new composite steels in cars will reduce the total vehicle weight. This is a major topic of interest in support of the general goal of reducing fuel consumption and CO2 emissions in future car designs.
Experimental conditions
Initially, the plate materials with a thickness of 2, 2,5 and 3mm were made of special continuous casting and hot and cold rolling (classical steel manufacturing method) by ARCELOR Research Group-France. The values of carbon and manganese are 0.04% and 0.40% respectively. Some of the steel sheets were welded only one fusion weld line by Gas Tungsten Arc (GTAW) process. Basically TiB2 ceramic particulates were used as reinforced materials in the iron matrix. All other details can be found easily in the documents [1, 2]. First of all, a detail metallographic analysis has been carried out. Evolution of TiB2 ceramic particulates were observed in the welded and base-metal parts. Secondly, micro hardness tests have been done on the polished metallographic specimens. In order to evaluate the toughness properties of the TiB2-RSMCs, impact -crash-tensile tests (ITT) have been carried out at different temperatures on the test specimens with a special geometry containing a smooth part (BM) and notched part (WM) with a special device mounted on an impact pendulum [7, 8]. Finally, static compressive tests, under a rigid spherical indenter with fixed radius (r = 3mm) have been carried out and the results were compared with that of the numerical analysis carried by using ABAQUS Code. Fracture and deformed surfaces of the sheet specimens were analysed by means of Scanning Electron Microscope (SEM) for understand the damage behaviour of the TiB2-RSMCs specimens under crash and static compression tests.
Results and Discussion
Microstructural evaluation
Different mechanisms due to the reinforcements in steel matrix were effective in the microstructure. This evaluation indicates the size effect and distribution of the ceramic particulates in the matrix. The morphology of the ceramic particulates and the matrix has been evaluated in metallurgical point of view. This information has allowed understanding the cohesion and wetability of the ceramic particulates with matrix. Generally, TiB2 ceramic particulates grew in hexagonal prismatic or rectangular shape. The micrograph given in Figure 1 shows the morphology and distribution of TiB2 reinforcements produced in steel matrix and eutectic structure in the weld bead. The details of microstructure evolution in Weld Metal – WM, and Heat Affected Zone, HAZ were discussed in former papers [2].
Fig. 1. Evolution of the microstructure of TiB2-RSMCs specimens in base metal (left) and weld bead (right)
In fact, solubility of iron in the TiB remains less than 4 % it means that system Fe/TiB keeps intact the mechanical properties of TiB . In the system Fe-B-Ti, TiB precipitates in steel by eutectic solidification (this avoids the primary precipitation of borides in the liquid metal). (Volume fraction is around 15 %, eutectic composition). These values were found with the surface percentages of the TiB2 ceramic particulates calculated by image analysis. Weld Bead, after solidification, gives regularly a dendritic structure. This type of structure is always developed around the ferrite nuclei.
Evaluation of micro hardness and impact tensile test behaviour
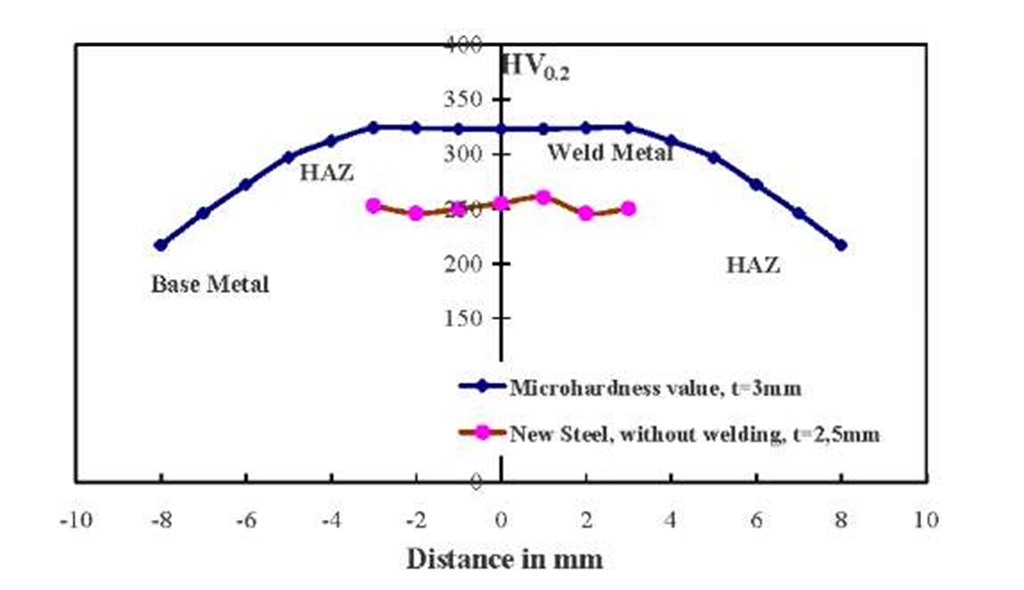
Micro hardness measurement was given in the Figure 2 as the mean values for three different zones (BM, HAZ, and WM). The values for the new steel sheets, without welding (only base metal), has been added in this diagram. The population of TiB2 particles distributed in the matrix plays an important role on the hardness evolution in the steel sheets.
Fig. 2. Hardness evolution in different parts of the steel sheets (WM, HAZ and Base metal)
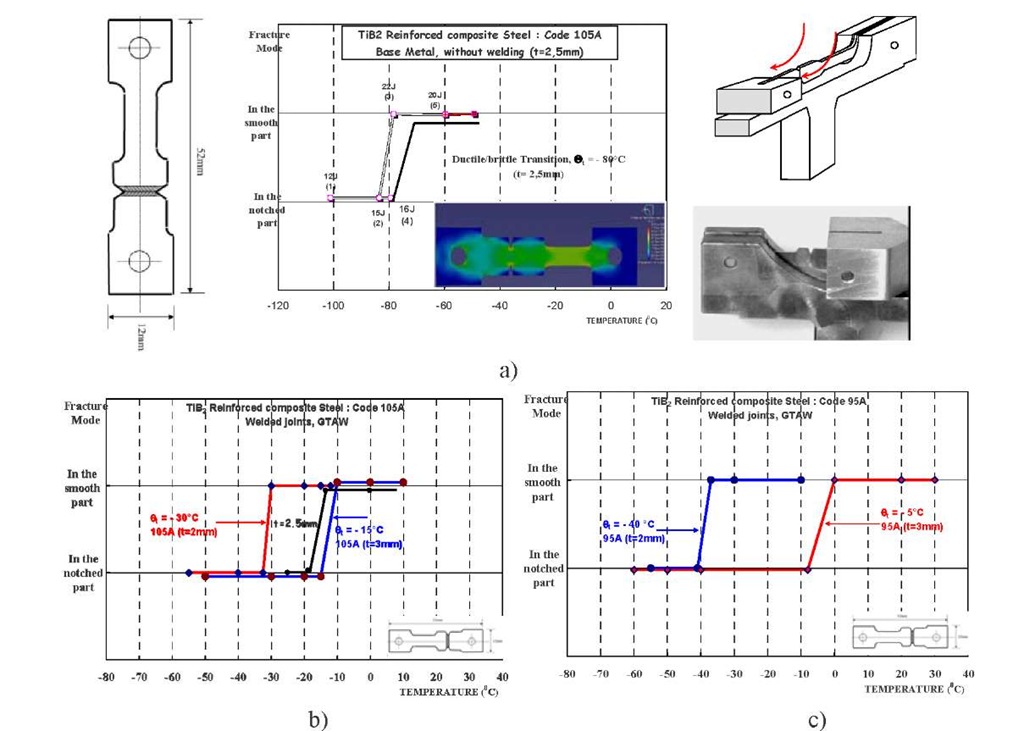
Impact tensile tests results were given in the Figure 3. All the details with this special test technique can be found in former works [2]. As indicated in the ductile – brittle transition behaviour of the test specimens are deeply different. As the base metal (without welding specimens in Figure 3a) gives a satisfaction transition values (around -80°C) the welded specimens show a transitions varying between -40 and -10°C depending on the thickness and also steel grades (Figure 3a and 3b). However, these results are very successful results for a steel matrix reinforced ceramic particles.
Fig. 3. Impact Tensile Test (ITT) results for the base metal and welded specimens with test device and developed specimen geometry and also FE stress distribution model with Abaqus stress analysis
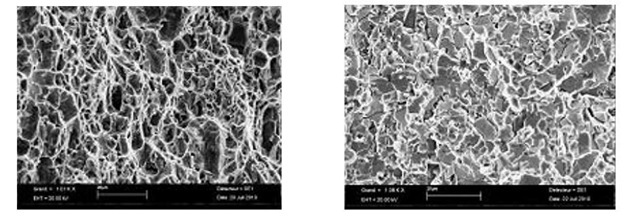
Evidently, fracture surfaces of these specimens verify these experimental results in case of the ductile and brittle failure conditions as indicated in Figure 4.
Fig.4. Impact tensile test results for the specimen failed in ductile (left) and brittle (right) fracture conditions
Compressive tests, under a rigid spherical indenter
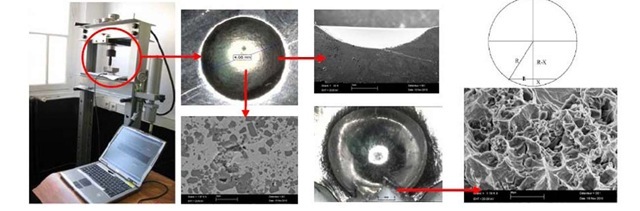
Static compression tests have been carried out under a rigid spherical indenter (r=3mm) and deformed zone areas were measured for each test specimen (only base metal) and fractographic analysis were also made for each specimen. This test is a typical damage test to understand the behaviour of the steel sheets containing ceramic reinforcements (Figure 5). The development of this product requires a better understanding of the relationship between crack propagation and microstructure. For this reason, a finite element based model was build which is inspired from the microstructure of the material. The micro hardness testing and the compressive tests are thus selected to compare between performances of this material based on experimental tests results and also numerical macro FE structural study. The dispersion of TiB2 particles in iron matrix is somewhat heterogeneous containing relatively regular shape of TiB2 particles.
Fig. 5. Static compression test under a rigid spherical indenter: deformed area on the sheet and fracture surface after deformation
Naturally, ITT and compression test carried out here as similar to the deep drawability tests cannot be positioned on the same plane. In other words, ITT characterises a ductile-brittle transition mode in fracture in dynamic loading conditions. So, it is sensitive to the physical parameters, which play a role on the cleavage (grain size, other defects, etc.). However, static compression test, of which ultimate stage is mostly the plastic failure, is mainly sensitive to the flow rule of materials during the deformation and also to the presence of particles of the second phase as indicated in these sheets reinforced with TiB2 ceramic particles. Meanwhile, to make a correlation between these two different test variables should be considered as an indicative presentation, because both of these tests reflect micro-structural parameters which influent both of these two type of tests. These parameters give practical information about the damage behaviour of these materials.
Microstructural Model and Finite Element (FE) simulations
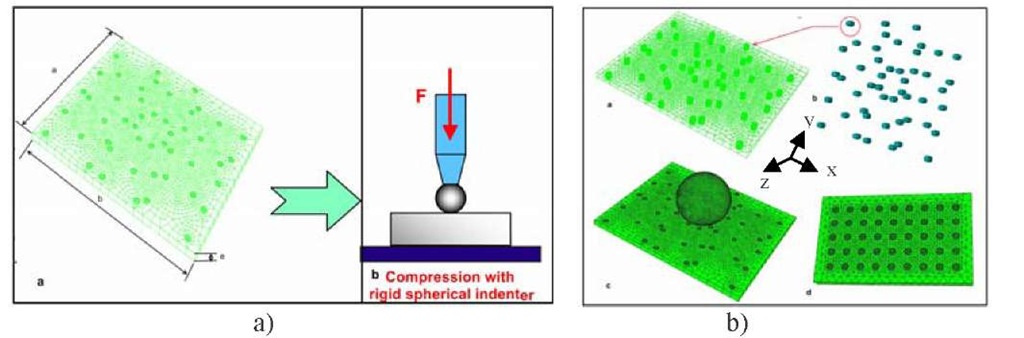
In order to understand well the stress strain mechanism of steel matrix composites reinforced with TiB2 ceramic particles, a finite element model (FEM) based on the actual microstructures was build. This model is stimulated from the micromechanical composition of the Fe-TiB2 as MMC material. Also, this model can provide the distribution of von Mises effective stress, strain and the maximum principal stress in the matrix and particles. The model is used to perform a comparison between experimental results and numerical results of compression tests. Figure 6 describes schematically the conditions of experimental compression tests, under a rigid spherical indenter with fixed radius (r = 3 mm). Geometric variables were illustrated used in this model and the geometry and mesh parameters were also used to analyse these experimental tests.
Fig. 6. Two-phases of steel matrix reinforced with TiB2 ceramic particles under deformation
The ideal microstructure considered in this study consists of a random arrangement of cylindrical inclusions (quasi hexagonal) embedded in a continuous steel matrix containing low carbon (Figure 7). The volume fraction of inclusions can vary from 10% to 20% and the micro-macro transition schemes are evaluated in many cases. However, when the volume fraction increases, nearby inclusions start to interact and this case influences the overall mechanical behaviour. Simulations must then be performed on a Representative Element Volume (REV) of the microstructure. Indeed, the spread of the macroscopic response for several distributions of various inclusions is lower than 5%. The generation of the random distribution follows rectangular cylinders filled with identical and aligned cylindrical inclusions. The RVE microstructure is periodic along the 3 directions, allowing us to apply periodic boundary conditions to the external faces of the specimens.
Fig.7. MMC Fe-TiB2 under compressive test a) FE model, b) the compressive scheme and b) different model parts and mesh representation
The inclusion positioning is constrained by the practical limitation of generating an acceptable FE mesh. A criterion is applied to the minimal distance between each inclusion surface and the external faces of the specimen. The volume of one particular cell inclusion is less then 1 mm3.
The representative cells are then meshed with quadratic tetrahedral elements. FE simulations are performed using ABAQUS (2008) and the whole volume is meshed using 4-node C3D4 tetrahedra in ABAQUS), enabling us to better capture the strain gradients in the matrix [12-14]. After that, a convergence study was successfully conducted by comparing the predictions (effective response and average inclusion response) to those obtained with finer meshes. The macroscopic stress predicted by the FE analysis is computed from a volume average of the stress tensor given at each integration point over the REV of domain "i":
Numerical procedure
The macroscopic stresses and strains values were aimed to compute using a homogenization procedure according to the Mori-Tanaka (M-T model) [12]. In fact, the computations of the matrix average stress and the macroscopic stresses are identical to the M-T model. The procedure is fully history-dependent, the deformation state at each integration point in the FE discretion as well as the current matrix average state depends on the corresponding state at the previous step time. Therefore, for any loading condition, even non-monotonic or non-proportional may be considered. The Mori-Tanaka scheme coupled with a FE solution of the equivalent inclusion problem. FE analysis provides an alternative approach for estimating the material properties. A FE model for the heterogeneous test is constructed in which the material parameters to be determined are considered as variable. The simulation is then performed and results are compared to data from a comparable experiment data set. The agreement between the model predictions and the data is quantified and judged to be sufficient or insufficient. If the agreement is not adequate, the parameter values are updated, a new FE model is created and run, and the process continues. Development of an effective parametric FE procedure requires automation of model creation, submission, results extraction, and comparison with experimental data. Within the context of Abaqus, the Python scripting language allows for such automation. The inclusion average stress may be directly extracted from the FE simulation using a Python script file. The computation of the average stress in each phase affects only the effective response of the composite, not the prediction of the stress-strain partitioning. This holds provided that all components of the macroscopic strain are given.
Here, a combination of tools was used to drive the optimization process. A Matlab interface was developed to create the Abaqus input file with all the necessary geometries, material parameter assignments, and also FE results acquisition. Python scripts were used to extract reaction forces, displacements and other variables from the output database, which were fed back into the Matlab process for comparison with the experimental data. The FE solution is used to simulate two-phase composites consisting of an elasto-plastic matrix reinforced by linear elastic inclusions. The predictions of the mean-field models are compared to reference results from FE computations on representative cells containing a random arrangement of multiple inclusions (Figure 7). Uniaxial and plane strain loading are successively applied to the multi-particle cells. The average of the macroscopic strain over a representative equivalent volume (REV) computed at each time step provides the loading history for the corresponding MF models. Therefore, results corresponding to the same macroscopic strain history, consistently with a strain homogenization procedure.
Average equivalent stress in the inclusions of two phase MMC material is determined for different volume fractions of the reinforcing phase. The multi-particle, FE predictions (FE with 20% volume fraction) correspond to a uniaxial compression test, while the predictions of the FE model are obtained imposing the same strain history as in the multi particle simulation.
Boundary conditions and material properties
The boundary condition is so set that at the bottom border as Ux, Uy, Uz = 0 and at the upper face of the specimen is imposed a negative displacement load Uy in y-direction via the rigid spherical or the plate indenter. A static step with small step time is used to assess the gradual evolution of stresses and strains in the elements model, the equivalent reaction force is calculated and used to furnishes the maximum load, when the deformation at the contact zone riches comparable value with the considered limited experimental one.
The mechanical Fe-TiB2 MMC material properties are derived from the particle inclusion properties of the TiB2 and those of pure iron as matrix. The inclusion material is assumed to be linearly elastic with elastic modulus Ep=300 GPa and Poisson’s ratio t> = 0.3. In the same way, iron is selected to be the metallic matrix with elastic modulus Em=210 GPa, Poisson’s ratio t>= 0.33. The inclusion average stress may be directly extracted from the FE simulation using a Python script file. The computation of the average stress in each phase influences only the effective response of the composite, not the prediction of the stress-strain partitioning. This holds provided that all of the components of the macroscopic strain are given. At this stage, a combination of tools was used to drive the calculation process.