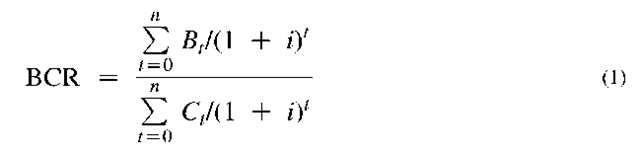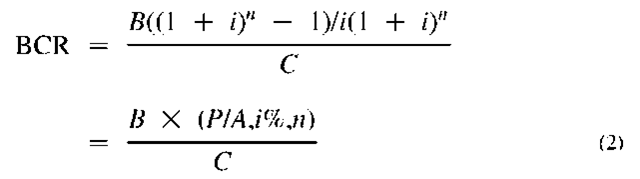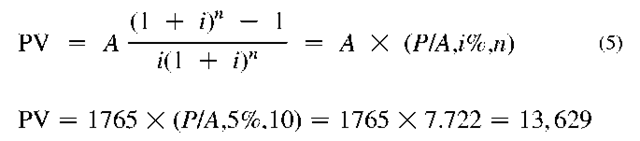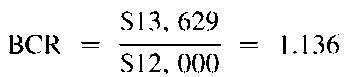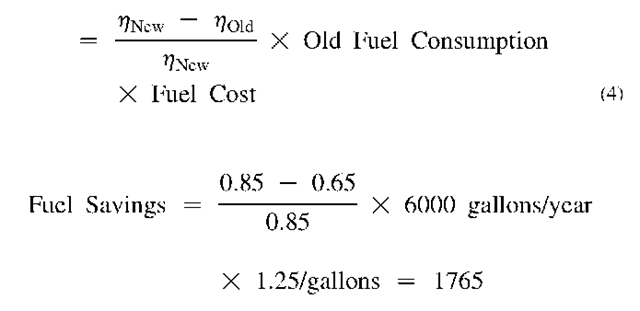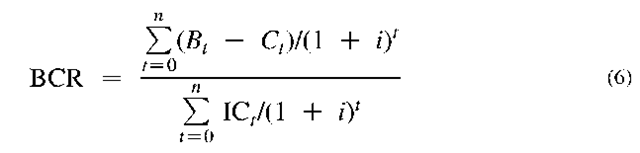Abstract
Benefit cost analysis is one of several methods utilized to evaluate the feasibility of capital investment. The benefit cost analysis calculates the present worth of all benefits, then calculates the present worth of all costs and takes the ratio of the two sums. This ratio is either known as a benefit/cost ratio, a savings/interest ratio, or a profitability index. The benefit cost analysis is an economic decision-making criterion that can measure the economic consequences of a decision over a specified period of time. It is used to evaluate whether an alternative option is economically viable when compared to a base case which is usually the “do nothing” option or it can be used to rank several options that are competing for a limited budget.
INTRODUCTION
The implementation of energy efficiency projects is linked to the allocation of funds. Economic decision-making tools or methods are often required to justify a project’s implementation and assess its economical feasibility. Several methods are available, such as life-cycle cost, simple or discounted payback, benefit cost analysis, and internal and adjusted rate-of-return.[1]
The selection of the method depends on many factors and, in fact, more than one method can be technically appropriate for economical decisions. These methods are often utilized to compare several options or to compare an alternative to the current situation usually referred to as the “do nothing” option. The American Society for Testing and Materials (ASTM) provides a guide that details the selection of economic methods for evaluating [2] investments.
This entry describes the economic assessment method known as benefit cost analysis (BCA). This method is simply considered as an attempt to identify and express, in dollar terms, all of the effects of proposed policies or projects and then to relate those effects with endured costs in a simple, dimensionless parameter.
BACKGROUND
Benefit cost analysis is one of the economic assessment methods that can aid policymakers in deciding whether the advantages of a particular course of action are likely to outweigh its drawbacks.
Benefit Cost Analysis
Benefit cost analysis was conceived over 150 years ago by the French engineer Jules Dupuit. The BCA method saw its first widespread use when the United States government wanted to evaluate the impact of water projects in the late 1930s. Since then, it has been used to analyze policies affecting several sectors including public health, transportation, criminal justice, education, defense, and the environment.[7]
The BCA method involves evaluating benefits of a project against its costs in a ratio format that is known as benefit-to-cost-ratio (BCR). Another variation of BCR is known as savings-to-investment-ratio (SIR). The difference between the two is that BCR is used when the focus of the analysis is on benefits (that is, advantages measured in dollars) relative to project costs while SIR is used when the focus of the assessment is on project savings (that is, cost reductions).[1] The BCR is referred to as the profitability index (PI) in some financial publications.[3] The estimation of a project’s PI is usually carried out based on the organization’s current net value of cash flows.
SIGNIFICANCE OF BCR
The BCR provides a standard for measuring economic performance in a single number that indicates whether a proposed project or system is preferred over a mutually exclusive alternative that serves as the baseline for the economic analysis. In addition, the BCR indicates the discounted dollar benefits (or savings) per dollar of discounted costs. Moreover, it can be used to determine if a given project or system is economically feasible relative to the alternative of not implementing it. Also, when computed on increments of benefits (or savings) and costs, the BCR can be used to determine if one design or size of a system is more economic than another. On the other hand, when funding is limited, the BCR can be used as an aid to select the most economically efficient set of projects from among several available options that are competing for limited funding. Selecting an efficient set of projects will maximize aggregate net benefits or net savings obtainable for the budget.[1] The BCR and the PI examine cash flows, not accounting profits, and recognize the time-value of money. While these ratios can be accurate predictors of economic efficiency, their accuracy depends on the accuracy of cash flow predictions.
PROCEDURE
Before conducting a BCA, multiple implementation alternatives should be identified in a way that allows for a fair comparison. The constraints or requirements of a successful end solution should be also clearly identified. Additionally, costs and benefits should be put into standard units (usually dollars) so that they can be compared directly. The dollar amounts used in the BCA should all be discounted, that is, expressed in time-equivalent dollars, either in present value or uniform annual value terms.
The BCR is a numerical ratio that indicates the expected economic performance of a project by the size of the ratio. A ratio less than 1.0 indicates a project that is uneconomic, a ratio of 1.0 indicates a project whose benefits or savings are just equal to its costs, and a ratio greater than 1.0 indicates a project that is economic.
The recommended steps for carrying out an economic evaluation using the BCA method are summarized as follows:
• Identification of objectives, constraints, and alternatives. The decision-maker’s objectives should be clearly specified. This is crucial to defining the problem. Moreover, constraints that limit potential alternatives for accomplishing the objectives should be identified such as economic and environmental limitations. Finally, alternatives that are technically and otherwise feasible in view of the constraints should be identified for consideration.
• Data collection. Actual or expected cash flows are needed for all phases of the project including revenues or other benefits; acquisition costs, including costs of planning, design, construction, purchase, installation, site preparation; utility costs, including costs of energy and operating and maintenance costs; repair and replacement costs; salvage values; disposal costs; and insurance costs. Moreover, information is also needed regarding the study period, discount rate, any applicable tax rates and rules, and the terms of financing (if applicable).
• Expression of cash flow. A decision should be made about whether to express the discounted cash flow of costs and benefits within each year in present-value dollars or in annual-value dollars. This should also include deciding whether to work in constant dollars using a real discount rate or in current dollars using a nominal discount rate. When using constant dollars, inflation is not included in the estimates of costs and benefits.[5]
• Compute the BCR or SIR. In concept, the BCA ratios are simple: benefits (or savings) divided by costs, where all dollar amounts are discounted to current or annual values. The BCR will be computed using the following formula:
Where Bt, benefits in period t; Ct, costs in period t; n, life of the investment; i, discount rate
Note that 1/(1 + i)’ is the discount factor used to calculate the present worth of a single future payment. Thus, to account for all future values, each value is calculated separately and then all values are added together. When evaluating an energy saving opportunity, its benefit at the beginning (at t = 0) will be zero, while for the following time periods the benefits (savings) will be evaluated separately. Usually, the costs will only be considered at t = 0 representing the initial cost. If the analysis will be carried out utilizing the uniform series of present worth as in the case of constant annual energy savings, then the following equation can be utilized to estimate the BCR:
Where B, annual benefits; C, initial cost; (PIA, i%, n), discount factor for a uniform series of cash flows
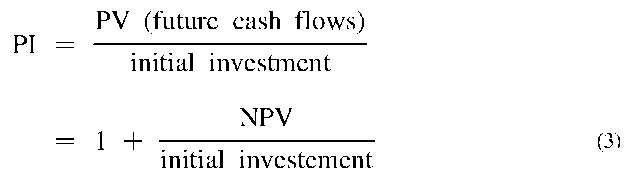
It should be noted that the BCR and PI represent the same parameter; and thus the PI can be calculated using Eq. 1. Alternatively Eq. 3 can be also used.
Where PV, Present value; NPV, Net present value of cash = benefits (inflows) — expenses (outflows)
Example 1
A building owner has $12,000 available to utilize for improvements. The owner is considering replacing the old together, the cash flows can be grouped into categories with the same pattern of occurrence and discounted using discount factors. In this case, since there is a uniform savings of $1,765 per year, the present value of the future annual cash flows is calculated using the following equation[8]:
Table 1 Cash flow details
| n (Year) | (1): Annual savings | (2): 1/(1+i)” | PV = (1)X (2) |
| 0 | 0 | 1 | 0 |
| 1 | 1765 | 0.952 | 1681 |
| 2 | 1765 | 0.907 | 1600.9 |
| 3 | 1765 | 0.864 | 1524.7 |
| 4 | 1765 | 0.823 | 1452.1 |
| 5 | 1765 | 0.784 | 1382.9 |
| 6 | 1765 | 0.746 | 1317.1 |
| 7 | 1765 | 0.711 | 1254.4 |
| 8 | 1765 | 0.677 | 1194.6 |
| 9 | 1765 | 0.645 | 1137.7 |
| 10 | 1765 | 0.614 | 1083.6 |
| 13,629 |
Where PV, present value of future annual cash flows; A, annual savings; (P/A, i%, n), discount factor for uniform series of cash flows. The values of this factor are listed in financial analysis topics. In this example, the value of (P/A, 5%, 10) = 7.722.[6]
The BCR using Eq. 2 will be calculated as:
boiler that has an efficiency of 65% with a new one that has an efficiency of 85%. Assuming that the lifespan of the boiler is 10 years and the discount rate is 5%, evaluate if this investment is cost-effective or not. The boiler uses oil and consumes 6000 gallons/year at a cost of $1.25 per gallon.
This example compares the option of using a new boiler to the “do nothing” option of using the old boiler. Accordingly, due to the higher efficiency of the new boiler, annual operational costs will be lower, assuming that the salvage values of the old boiler and the new one are insignificant.
The annual savings due to the new boiler’s efficiency improvement are calculated using the following equation[4]:
Fuel Savings
The cash flows are detailed in Table 1, and are calculated year by year.
An alternative option to estimating the present worth of future savings would be to use a uniform series present worth factor. This is done for ease of calculation. Instead of discounting the amounts in each year and adding them.Since the BCR is more than one, this means that the benefits outweigh the costs; hence, the boiler replacement is financially justified.
• In practice, it is important to formulate the ratio so as to satisfy the investor’s objective. This requires attention to the placement of costs in the numerator and denominator. To maximize net benefits from a designated expenditure, it is necessary to place only that portion of costs in the denominator on which the investor wishes to maximize returns. Then, the BCR will be computed using the following formula:
Where Bt, benefits in period t; that is, the advantages in revenue or performance (measured in dollars) of the building or system as compared to a mutually exclusive alternative; Ct, costs in period t, excluding investment costs that are to be placed in the denominator for the building or system, minus counterpart costs in period t for a mutually exclusive alternative; IQ, investment costs in period t on which the investor wishes to maximize the return, minus similar investment costs in period t for a mutually exclusive alternative; i, discount rate.
Special attention should be paid when placing cost and benefit items into the ratio especially in the case when several projects are compared and a ranking of their cost-effectiveness needs to be established. Changing the placement of a cost item from the denominator (where it increases costs) to the numerator (where it decreases benefits or savings) will affect the relative rankings of competing independent projects, and thereby influence investment decisions.[1] • Biasing effects, detrimental to economic efficiency, can result from certain formulations of the BCR and SIR ratios. As an example, when comparing competing projects that differ significantly in their maintenance costs, placing maintenance costs in the denominator with investment costs tends to bias the final selection away from projects with relatively high maintenance costs, even though they may offer higher net benefits (profits) than competing projects. Similar biasing effects can occur in the placement of other non-investment costs such as energy or labor costs. This highlights the fact that adding a given amount to the denominator of a ratio reduces the quotient more than does subtracting an identical amount from the numerator. Hence, to eliminate this bias when the objective is to maximize the return on the investment budget, all non-investment costs should be placed in the numerator.[1]
Table 3 Projects ranked by initial cost
| Project number | Initial cost | NPV | PI |
| 1 | 430,000 | 250,500 | 1.583 |
| 2 | 380,000 | 215,000 | 1.566 |
| 3 | 310,000 | 40,000 | 1.129 |
| 4 | 260,000 | 60,000 | 1.231 |
| 5 | 230,000 | 310,000 | 2.348 |
| 6 | 185,000 | 105,000 | 1.568 |
| 7 | 135,000 | 125,000 | 1.926 |
| 8 | 110,000 | 76,000 | 1.691 |
| 9 | 90,000 | 122,000 | 2.356 |
| 10 | 85,000 | 96,000 | 2.129 |
PROJECT SELECTION UNDER CAPITAL RATIONING
When a firm needs to decide whether to invest in certain projects, the net present value (NPV) method is commonly used. In this method, all of the present values of both cash inflows and outflows are accounted for, and the difference in the values represents the NPV. A higher NPV reflects better rewards and higher benefits. If a firm wants to select the best of new projects within a limited budget, then it should choose the set of projects that provides the largest total NPV. Here the BCA can be a useful tool for identifying the best projects to choose under the capital rationing method.[3] This is because the BCA normalizes the evaluation as it measures the NPV per dollar invested regardless of the project size. The following two examples illustrate the selection procedure for projects under capital rationing.
Example 2
In Table 2, several energy conservation measures are assessed in terms of their economic viability. It is required to select the optimum alternative, but also to maintain the budget constraint that states that only $14,000 is available as a capital investment. Assume that the lifespan of the energy conservation measures is 15 years and the discount rate is 5%.
The BCR values are calculated utilizing the present value of money and listed in Table 2. The highest BCR value was that of the R-15 wall insulation (Alternative B), followed by R-10 wall insulation (Alternative A), and then reflective glass (Alternative F). All other measures had BCR values below 1, which means that the returns on investment in these energy conservation measures will not pay for themselves after 15 years. Due to the budget constraint, Alternatives A and F with a total cost of $13,570 represent the optimum alternatives. If the available budget was $15,000 instead of $14,000 then
Table 2 Investment details among alternative projects
| Project code | (1) Project description | (2) Project cost PV ($) | (3) Energy savings PV ($) | (4) BCR | (5) Ranking | (6) Net benefits | (7) PI |
| 1 A | Wall R-10 | 6,050 | 12,000 | 1.983 | 2 | 5950 | 1.983 |
| B | Wall R-15 | 6,900 | 13,800 | 2.000 | 1 | 6900 | 2.000 |
| C | Roof R-15 | 7,200 | 5,000 | 0.694 | 5 | - 2200 | 0.694 |
| D | Roof R-20 | 7,500 | 5,700 | 0.760 | 4 | -1800 | 0.760 |
| E | Double glass | 6,300 | 4,100 | 0.651 | 6 | - 2200 | 0.651 |
| F | Reflective | 7,520 | 10,000 | 1.330 | 3 | 2480 | 1.330 |
| glass |
Note: (4) = (3)/(2), (6) = (3)- (2) and (7) = 1 + (6)/(2).
Alternatives B and F, with a total cost of $14,420, can be selected.
Example 3
A company has a maximum of $1.5 million to invest in retrofitting old buildings to reduce their energy consumption. After evaluating numerous projects, only those that are listed in Table 3 were selected to analyze. Unfortunately, to undertake all these projects a total fund of $2.215 million is required. Accordingly, a decision has to be made to stay within the budget constraint.
The projects in Table 4 are ranked in descending order by their PI. A higher PI is more desirable than the lower one as it creates more NPV per dollar of the initial investment.
Given this scenario (and keeping in mind the budget constraint of $1.5 million), projects 9, 5, 10, 7, 8, 1, and 6 will be selected. The total accumulative cost of these projects amounts to $1.265 million with a cumulative NPV of $1.0845 million. On the other hand, when skipping project 1 and going down the list to include projects 2 and 4, the cumulative initial cost amounts to $1.475 with an NPV of $1.109. The NPV of the second group of projects was higher than that of the first group. This means that the second group will provide a more economic solution.
Table 4 Profitability index for project selection
Cumulative
| Project number | Initial cost | NPV | PI | Cost | NPV | Cost | NPV |
| 9 | 90,000 | 122,000 | 2.36 | 90,000 | 122,000 | 90,000 | 122,000 |
| 5 | 230,000 | 310,000 | 2.35 | 320,000 | 432,000 | 320,000 | 432,000 |
| 10 | 85,000 | 96,000 | 2.13 | 405,000 | 528,000 | 405,000 | 528,000 |
| 7 | 135,000 | 125,000 | 1.93 | 540,000 | 653,000 | 540,000 | 653,000 |
| 8 | 110,000 | 76,000 | 1.69 | 650,000 | 729,000 | 650,000 | 729,000 |
| 1 | 430,000 | 250,500 | 1.58 | 1,080,000 | 979,500 | ||
| 6 | 185,000 | 105,000 | 1.57 | 1,265,000 | 1,084,500 | 835,000 | 834,000 |
| 2 | 380,000 | 215,000 | 1.57 | 1,645,000 | 1,299,500 | 1,215,000 | 1,049,000 |
| 4 | 260,000 | 60,000 | 1.23 | 1,905,000 | 1,359,500 | 1,475,000 | 1,109,000 |
| 3 | 310,000 | 40,000 | 1.13 | 2,215,000 | 1,399,500 | 1,785,000 | 1,149,000 |
• If the outcome appears particularly sensitive to the value assigned to a given parameter, and the estimate is of poor or unknown quality, the analyst may wish to improve the quality of the data. Sensitivity analysis, a useful technique for identifying critical parameters, should be carried out accordingly.
• Alternatives must be compared over the same study period; otherwise, asset values including costs and savings (benefits) may be repeated.
• NPV and PI will always yield the same decision, though they will not necessarily rank projects in the same order.
CONCLUSION
Several points should be considered when conducting BCA.
• The outcome of any analysis will vary depending on the data estimates and assumptions. Thus, it is important to carefully select the assumed values for critical parameters such as the discount rate values to arrive at a realistic solution.