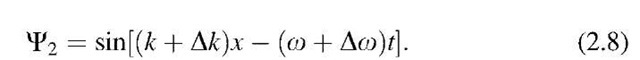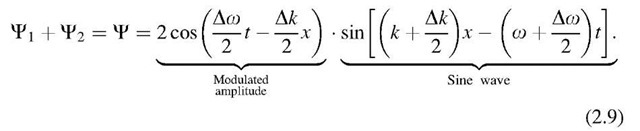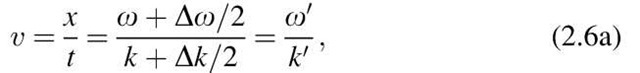This topic is mainly concerned with the interactions of electrons with matter. Thus, the question "What is an electron?" is quite in order. Now, to our knowledge, nobody has so far seen an electron, even by using the most sophisticated equipment. We experience merely the actions of electrons, e.g., on a cathode-ray television screen or in an electron microscope. In each of these instances, the electrons seem to manifest themselves in quite a different way, i.e., in the first case as a particle and in the latter case as an electron wave. Accordingly, we shall use, in this topic, the terms "wave" and "particle" as convenient means to describe the different aspects of the properties of electrons. This "duality" of the manifestations of electrons should not overly concern us. The reader has probably been exposed to a similar discussion when the properties of light have been introduced.
We perceive light intuitively as a wave (specifically, an electromagnetic wave) which travels in undulations from a given source to a point of observation. The color of the light is related to its wavelength, l, or to its frequency, n, i.e., its number of vibrations per second. Many crucial experiments, such as diffraction, interference, and dispersion clearly confirm the wavelike nature of light. Nevertheless, at least since the discovery of the photoelectric effect in 1887 by Hertz, and its interpretation in 1905 by Einstein, we do know that light also has a particle nature. (The photoelectric effect describes the emission of electrons from a metallic surface that has been illuminated by light of appropriately high energy, e.g., by blue light.) Interestingly enough, Newton, about 300 years ago, was a strong proponent of the particle concept of light. His original ideas, however, were in need of some refinement, which was eventually provided in 1901 by quantum theory. We know today (based on Planck’s famous hypothesis) that a certain minimal energy of light, i.e., at least one light quantum, called a photon, with the energy
needs to impinge on a metal in order that a negatively charged electron may overcome its binding energy to its positively charged nucleus and escape into free space. (This is true regardless of the intensity of the light.) In (2.1) h is the Planck constant whose numerical value is given in topic 4. Frequently, the reduced Planck constant
is utilized in conjunction with the angular frequency, o = 2nv (1.7). In short, the wave-particle duality of light (or more generally, of electromagnetic radiation) had been firmly established at the beginning of the twentieth century.
On the other hand, the wave-particle duality of electrons needed more time until it was fully recognized. The particle property of electrons, having a rest mass m0 and charge e, was discovered in 1897 by the British physicist J.J. Thomson at the Cavendish Laboratory of Cambridge University in an experiment in which he observed the deviation of a cathode ray by electric and magnetic fields. These cathode rays were known to consist of an invisible radiation that emanated from a negative electrode (called a cathode) which was sealed through the walls of an evacuated glass tube that also contained at the opposite wall a second, positively charged electrode. It was likewise known at the end of the nineteenth century that cathode rays travel in straight lines and produce a glow when they strike glass or some other materials. J.J. Thomson noticed that cathode rays travel slower than light and transport negative electricity. In order to settle the lingering question of whether cathode rays were "vibrations of the ether" or instead "streams of particles", he promulgated a bold hypothesis, suggesting that cathode rays were "charged corpuscles which are miniscule constituents of the atom". This proposition—that an atom should consist of more than one particle—was startling for most people at that time. Indeed, atoms were considered since antiquity to be indivisible, that is, the most fundamental building blocks of matter.
The charge of these "corpuscles" was found to be the same as that carried by hydrogen ions during electrolysis (about 10-19 C). Further, the mass of these corpuscles turned out to be 1/2000th the mass of the hydrogen atom.
A second hypothesis brought forward by J.J. Thomson, suggesting that the "corpuscles of cathode rays are the only constituents of atoms", was eventually proven to be incorrect. Specifically, E. Rutherford, one of Thomson’s former students, by using a different kind of particle beam, concluded in 1910 that the atom resembled a tiny solar system in which a few electrons orbited around a "massive" positively charged center. Today, one knows that the electron is the lightest stable elementary particle of matter and that it carries the basic charge of electricity.
Eventually, it was also discovered that the electrons in metals can move freely under certain circumstances. This critical experiment was performed by Tolman who observed inertia effects of the electrons when rotating metals.
In 1924, de Broglie, who believed in a unified creation of the universe, introduced the idea that electrons should also possess a wave-particle duality. In other words, he suggested, based on the hypothesis of a general reciprocity of physical laws, the wave nature of electrons. He connected the wavelength, l, of an electron wave and the momentum, p, of the particle by the relation
This equation can be "derived" by combining equivalents to the photonic equations E = nh (2.1), E = mc2 (1.8), p = mc (1.3), and c = In (1.5).
In 1926, Schrodinger gave this idea of de Broglie a mathematical form. In 1927, Davisson and Germer and, independently in 1928, G.P. Thomson (the son of J.J. Thomson; see above) discovered electron diffraction by a crystal, which finally proved the wave nature of electrons.
What is a wave? A wave is a "disturbance" which is periodic in position and time. (In contrast to this, a vibration is a disturbance which is only periodic in position or time.1) Waves are characterized by a velocity, v, a frequency, n, and a wavelength, l, which are interrelated by
Quite often, however, the wavelength is replaced by its inverse quantity (multiplied by 2p), i.e., l is replaced by the wave number
Concomitantly, the frequency, n, is replaced by the angular frequency o = 2 pn (1.7). Equation (2.4) then becomes
One of the simplest waveforms is mathematically expressed by a sine (or a cosine) function. This simple disturbance is called a "harmonic wave". (We restrict our discussion below to harmonic waves since a mathematical manipulation, called a Fourier transformation, can substitute any odd type of waveform by a series of harmonic waves, each having a different frequency.)
The properties of electrons will be described in the following by a harmonic wave, i.e., by a wave function C (which contains, as outlined above, a time- and a space-dependent component):
This wave function does not represent, as far as we know, any physical waves or other physical quantities. It should be understood merely as a mathematical description of a particle (the electron) which enables us to calculate its actual behavior in a convenient way. This thought probably sounds unfamiliar to a beginner in quantum physics. However, by repeated exposure, one can become accustomed to this kind of thought.
The wave-particle duality may be better understood by realizing that the electron can be represented by a combination of several wave trains having slightly different frequencies, for example, o and o + Do, and different wave numbers, k and k + Dk. Let us study this, assuming at first only two waves, which will be written as above:
Superposition of![]() yields a new wave
yields a new wave![]() With
With![]()
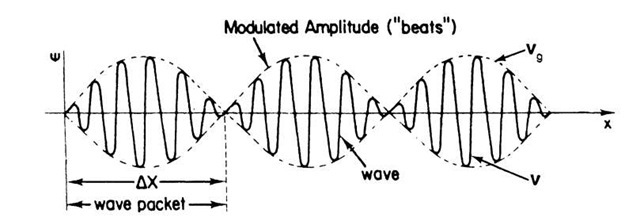
Equation (2.9) describes a sine wave (having a frequency intermediate between o and o + Do) whose amplitude is slowly modulated by a cosine function. (This familiar effect in acoustics can be heard in the form of "beats" when two strings of a piano have a slightly different pitch. The beats become less rapid the smaller the difference in frequency, Do, between the two strings until they finally cease once both strings have the same pitch, (2.9).) Each of the "beats" represents a "wave packet" (Fig. 2.1). The wave packet becomes "longer" the slower the beats, i.e., the smaller Do. The extreme conditions are as follows:
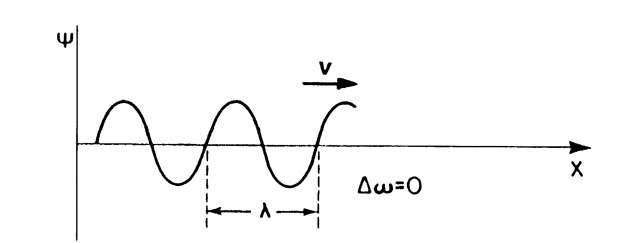
(a) No variation in o and k (i.e., Do = 0 and Dk = 0). This yields an "infinitely long" wave packet, i.e., a monochromatic wave, which corresponds to the wave picture of an electron (see Fig. 2.2).
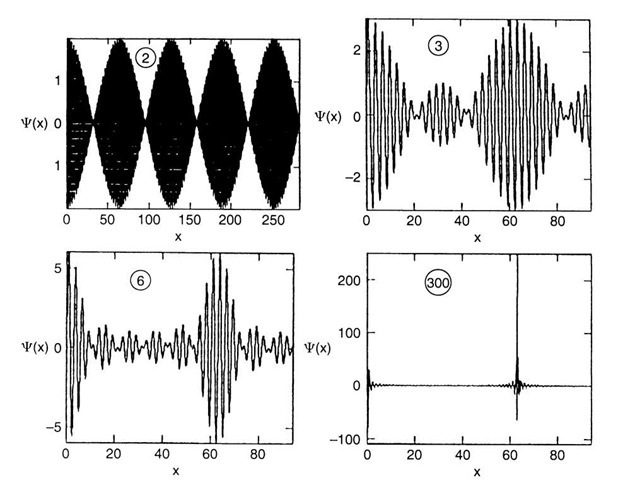
(b) Alternately, Do and Dk could be assumed to be very large. This yields short wave packets. Moreover, if a large number of different waves are combined (rather than only two waves C1 and C2), having frequencies o + nDo (where n = 1, 2, 3, 4,…), then the string of wave packets shown in Fig. 2.1 reduces to one wave packet only.
Figure 2.1. Combination of two waves of slightly different frequencies. DX is the distance over which the particle can be found.
Figure 2.2. Monochromatic matter wave (Do and Dk = 0). The wave has constant amplitude. The matter wave travels with the phase velocity, v.
The electron is then represented as a particle. This is shown in Fig. 2.3, in which a number of C-waves have been superimposed on each other, as just outlined. It is evident from Fig. 2.3 that a superposition of, say, 300 C-waves yields essentially one wave packet only.
Different velocities need to be distinguished:
(a) The velocity of the matter wave is called the wave velocity or "phase velocity", v. As we saw above, the matter wave is a monochromatic wave (or a stream of particles of equal velocity) whose frequency, o, wave-length, l, momentum, p, or energy, E, can be exactly determined (Fig. 2.2). The location of the particles, however, is undetermined. From the second part of (2.9) (marked "sine wave"), we deduce
which is a restatement of (2.6). We obtain the velocity of a matter wave that has a frequency o + Do/2 and a wave number k + Dk/2. The phase velocity varies for different wavelengths (a phenomenon which is called "dispersion", and which the reader knows from the rainbow colors that emerge from a prism when white light impinges on it).
Figure 2.3. Superposition of C-waves. The number of C-waves is given in the graphs.
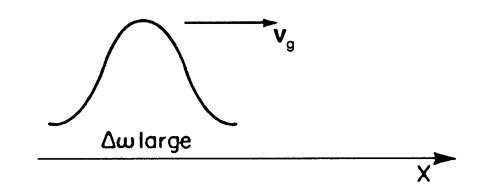
(b) We mentioned above that a particle can be understood to be "composed of" a group of waves or a "wave packet". Each individual wave has a slightly different frequency. Appropriately, the velocity of a particle is called "group velocity", vg. The "envelope" in Fig. 2.1 propagates with the group velocity, vg. From the left part of (2.9) (marked "modulated amplitude") we obtain this group velocity
Equation (2.10) is the velocity of a "pulse wave", i.e., of a moving particle.
The location X of a particle is known precisely, whereas the frequency is not. This is due to the fact that a wave packet can be thought to "consist" of several wave functions![]() with slightly different frequencies. Another way of looking at it is to perform a Fourier analysis of a pulse wave (Fig. 2.4) which results in a series of sine and cosine functions (waves) which have different wavelengths. The better the location, DX, of a particle can be stating that the product of the distance over which there is a finite probability of finding an electron, DX, and the range of momenta, Dp (or wave-lengths (2.3)), of the electron wave is greater than or equal to a constant.
with slightly different frequencies. Another way of looking at it is to perform a Fourier analysis of a pulse wave (Fig. 2.4) which results in a series of sine and cosine functions (waves) which have different wavelengths. The better the location, DX, of a particle can be stating that the product of the distance over which there is a finite probability of finding an electron, DX, and the range of momenta, Dp (or wave-lengths (2.3)), of the electron wave is greater than or equal to a constant.
Figure 2.4. Particle (pulse wave) moving with a group velocity vg (Do is large).
This means that both the location and frequency of an electron cannot be accurately determined at the same time.
A word of encouragement should be added at this point for those readers who (quite legitimately) might ask the question: What can I do with wave functions which supposedly have no equivalent in real life? For the interpretation of the wave functions, we will use in future topics Born’s postulate, which states that the square of the wave function (or because C is generally a complex function, the quantity CC ) is the probability of finding a particle at a certain location. (C is the complex conjugate quantity of C.) In other words,
is the probability of finding an electron in the volume element dt. This makes it clear that in wave mechanics probability statements are often obtained, whereas in classical mechanics the location of a particle can be determined exactly. We will see in future topics, however, that this does not affect the usefulness of our results.
Finally, the reader may ask the question: Is an electron wave the same as an electromagnetic wave? Most definitely not! Electromagnetic waves (radio waves, infrared radiation (heat), visible light, ultraviolet (UV) light, X-rays, or g-rays) propagate by an interaction of electrical and magnetic disturbances. Detection devices for electromagnetic waves include the human eye, photomultiplier tubes, photographic films, heat-sensitive devices, such as the skin, and antennas in conjunction with electrical circuits. For the detection of electrons (e.g., in an electron microscope or on a television screen) certain chemical compounds called "phosphors" are utilized. Materials which possess "phosphorescence" (see Section 13.8) include zinc sulfide, zinc-cadmium sulfide, tungstates, molybdates, salts of the rare earths, uranium compounds, and organic compounds.
At the end of this topic, let us revisit the fundamental question that stood at the outset of our discussion concerning the wave-particle duality: Are particles and waves really two completely unrelated phenomena? Seen conceptually, they probably are. But consider (2.9) and its discussion. Both waves and particles are mathematically described essentially by the same equation, i.e., the former by setting Do and Dk = 0 and the latter by making Do and Dk large. Thus, waves and particles appear to be interrelated in a certain way. It is left to the reader to contemplate further on this idea.