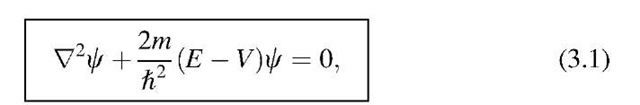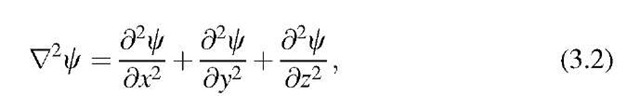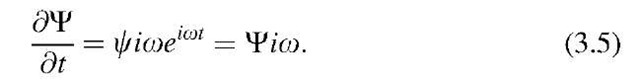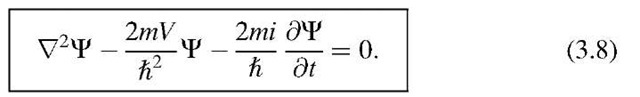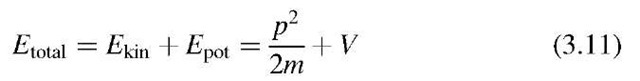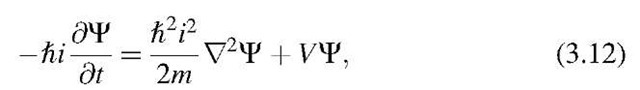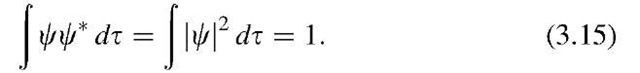We shall now make use of the conceptual ideas which we introduced in the previous topic, i.e., we shall cast, in mathematical form, the description of an electron as a wave, as suggested by Schrodinger in 1926. All "derivations" of the Schrodinger equation start in one way or another from certain assumptions, which cause the uninitiated reader to ask the legitimate question, "Why just in this way?" The answer to this question can naturally be given, but these explanations are relatively involved. In addition, the "derivations" of the Schrodinger equation do not further our understanding of quantum mechanics. It is, therefore, not intended to "derive" here the Schroodinger equation. We consider this relation as a fundamental equation for the description of wave properties of electrons, just as the Newton equations describe the matter properties of large particles.
The Time-Independent Schrodinger Equation
The time-independent Schrodinger equation will always be applied when the properties of atomic systems have to be calculated in stationary conditions, i.e., when the property of the surroundings of the electron does not change with time. This is the case for most of the applications which will be discussed in this text. Thus, we introduce, at first, this simpler form of the Schrodinger equation in which the potential energy (or potential barrier), V, depends only on the location (and not, in addition, on the time). Therefore, the time-independent Schrodinger equation is an equation of a vibration. It has the following form:
where
and m is the (rest) mass of the electron,2 and
is the total energy of the system. E provides values for allowed energies once C and V are given, as we shall see later on.
In (3.1) we wrote for the wave function a lowercase C, which we will use from now on when we want to state explicitly that the wave function is only space dependent. Thus, we split from C a time-dependent part:
The Time-Dependent Schrodinger Equation
The time-dependent Schrodinger equation is a wave equation, because it contains derivatives of C with respect to space and time (see below, (3.8)). One obtains this equation from (3.1) by eliminating the total energy,
where o is obtained by differentiating (3.4) with respect to time:
This yields
Combining (2.1) with (3.6) provides
Finally, combining (3.1) with (3.7) yields
It should be noted here that quantum mechanical equations can be obtained from classical equations by applying differential operators to the wave function C (Hamiltonian operators). They are
and
When these operators are applied to
we obtain
which yields, after rearranging, the time-dependent Schrodinger equation (3.8).
Special Properties of Vibrational Problems
The solution to an equation for a vibration is determined, except for certain constants. These constants are calculated by using boundary or starting conditions
As we will see in Section 4.2, only certain vibrational forms are possible when boundary conditions are imposed. This is similar to the vibrational forms of a vibrating string, where the fixed ends cannot undergo vibrations. Vibrational problems that are determined by boundary conditions are called boundary or eigenvalue problems. It is a peculiarity of vibrational problems with boundary conditions that not all frequency values are possible and, therefore, because of
not all values for the energy are allowed (see next topic). One calls the allowed values eigenvalues. The functions C, which belong to the eigenvalues and which are a solution of the vibration equation and, in addition, satisfy the boundary conditions, are called eigenfunctions of the differential equation.
In Section 2 we related the product CC (which is called the "norm") to the probability of finding a particle at a given location. The probability of finding a particle somewhere in space is one, or
Equation (3.15) is called the normalized eigenfunction.