Solution of the Schrodinger Equation for Four Specific Problems (Fundamentals of Electron Theory) Part 3

Electron in a Periodic Field of a Crystal (The Solid State)

In the preceding sections we became acquainted with some special cases, namely, the completely free electron and the electron which is confined to a potential well. The goal of this section is to study the behavior of an electron in a crystal. We will see eventually that the extreme cases which we treated previously can be derived from this general case.

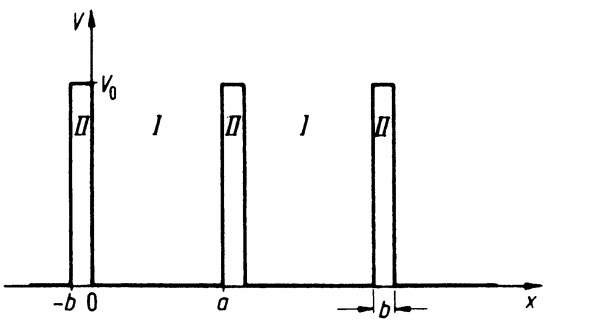
Our first task is to find a potential distribution that is suitable for a solid. From high resolution transmission electron microscopy and from X-ray diffraction investigations, it is known that the atoms in a crystal are arranged periodically. Thus, for the treatment of our problem a periodic repetition of the potential well of Fig. 4.2, i.e., a periodic arrangement of potential wells and potential barriers, is probably close to reality and is also best suited for a calculation. Such a periodic potential is shown in Fig. 4.9 for the one-dimensional case.4

The potential distribution shows potential wells of length a, which we call Region I. These wells are separated by potential barriers of height V0 and width b (Region II), where V0 is assumed to be larger than the energy E of the electron.

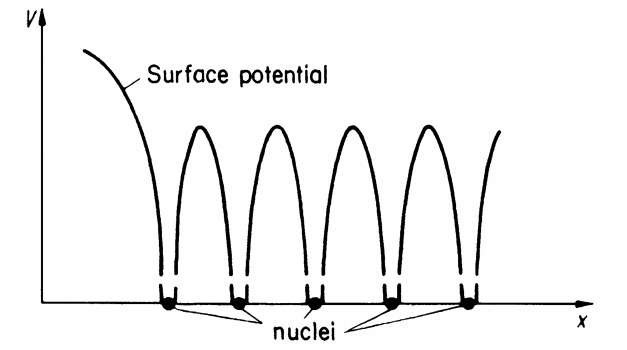
This model is certainly a coarse simplification of the actual potential distribution in a crystal. It does not take into consideration that the inner electrons are more strongly bound to the core, i.e., that the potential function of a point charge varies as 1/r. It also does not consider that the individual potentials from each lattice site overlap. A potential distribution which takes these features into consideration is shown in Fig. 4.10. It is immediately evident, however, that the latter model is less suitable for a simple calculation than the one which is shown in Fig. 4.9. Thus, we utilize the model shown in Fig. 4.9.

Figure 4.9. One-dimensional periodic potential distribution (simplified) (Kronig-Penney model).

Figure 4.10. One-dimensional periodic potential distribution for a crystal (muffin tin potential).

We now write the Schrodinger equation for Regions I and II:

For abbreviation we write, as before,

and

(g2 is chosen in a way to keep it from becoming imaginary, see Section 4.3.) Equations (4.44) and (4.45) need to be solved simultaneously, a task which can be achieved only with considerable mathematical effort. Bloch5 showed that the solution of this type of equation has the following form:

(Bloch function), where u(x) is a periodic function which possesses the periodicity of the lattice in the x-direction. Therefore, u(x) is no longer a constant (amplitude A) as in (4.2), but changes periodically with increasing x (modulated amplitude). Of course, u(x) is different for various directions in the crystal lattice.

The reader who is basically interested in the results, and their implications for the electronic structure of crystals, may skip the mathematical treatment given below and refer directly to (4.67).

Differentiating the Bloch function (4.48) twice with respect to x provides

We insert (4.49) into (4.44) and (4.45) and take into account the abbreviations (4.46) and (4.47):

Equations (4.50) and (4.51) have the form of an equation of a damped vibration. The solution6 to (4.50) and (4.51) is

We have four constants A, B, C, and D which we need to dispose of by means of four boundary conditions: The functions C and dC/dx pass over continuously from Region I into Region II at the point x = 0. Equation I = Equation II for x = 0 yields

(du/dx) for I = (du/dx) for II at x = 0 provides

Further, C, and therefore u, is continuous at the distance (a + b). This means that Equation I at x = 0 must be equal to Equation II at x = a + b, 6Differential equation of a damped vibration for spatial periodicity (see topic 1)

Solution:

where

or, more simply, Equation I at x = a is equal to Equation II at x = —b (see Fig. 4.9). This yields

Finally, (du/dx) is periodic in a + b:

The constants A, B, C, and D can be determined by means of these four equations which, when inserted in (4.55) and (4.56), provide values for u. This also means that solutions for the function C can be given by using (4.48). However, as in the preceding sections, the knowledge of the C function is not of primary interest. We are searching instead for a condition which tells us where solutions to the Schrodinger equations (4.44) and (4.45) exist. We recall that these limiting conditions were leading to the energy levels in Section 4.2. We proceed here in the same manner. We use the four equations (4.57)-(4.60) and eliminate the four constants A-D. (This can be done by simple algebraic manipulation or by forming the determinant out of the coefficients A-D and equating this determinant to zero). The lengthy calculation provides, using some Euler equations,7

For simplification of the discussion of this equation we make the following stipulation. The potential barriers in Fig. 4.9 will be of the kind such that b is very small and V0 is very large. It is further assumed that the product V0b, i.e., the area of this potential barrier, remains finite. In other words, if V0 grows, b diminishes accordingly. The product V0b is called the potential barrier strength.

If V0 is very large, then E in (4.47) can be considered to be small compared to V0 and can therefore be neglected so that

Multiplication of (4.62) by b yields

Since V0b has to remain finite (see above) and b ! 0 it follows that gb becomes very small. For a small gb we obtain (see tables of the hyperbolic functions)

Finally, one can neglect a2 compared to g2 and b compared to a (see (4.46), (4.47), and Fig. 4.9) so that (4.61) reads as follows:

With the abbreviation

we finally get from (4.65)

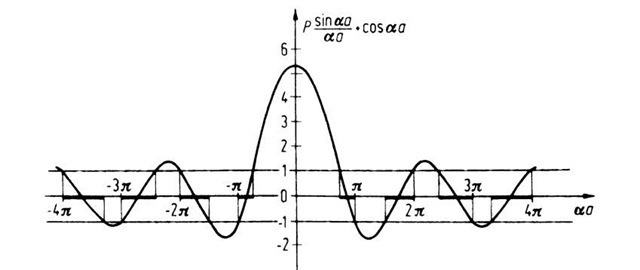
This is the desired relation which provides the allowed solutions to the Schrodinger equations (4.44) and (4.45). We notice that the boundary conditions lead to an equation with trigonometric function similarly as in Section 4.2. Therefore, only certain values of a are possible. This in turn means, because of (4.46), that only certain values for the energy E are defined. One can assess the situation best if one plots the function P(sin aa/aa) + cos a a versus a a, which is done in Fig. 4.11 for P = (3/2)p. It is of particular significance that the right-hand side of (4.67) allows only certain values of this function because cos ka is only defined between +1 and —1 (except for imaginary k-values). This is shown in Fig. 4.11, in which the allowed values of the function P(sin aa/aa) + cos a a are marked by heavy lines on the aa-axis.

We arrive herewith at the following very important result: Because aa is a function of the energy, the above-mentioned limitation means that an electron that moves in a periodically varying potential field can only occupy certain allowed energy zones. Energies outside of these allowed zones or "bands" are prohibited.

Figure 4.11. Function P(sin aa/aa) + cos a a versus a a. P was arbitrarily set to be (3/2)p.

One sees from Fig. 4.11 that with increasing values of aa (i.e., with increasing energy), the disallowed (or forbidden) bands become narrower. The size of the allowed and forbidden energy bands varies with the variation of P. Below, four special cases will be discussed.

(a) If the "potential barrier strength" V0b (see Fig. 4.9) is large, then, according to (4.66), P is also large and the curve in Fig. 4.11 proceeds more steeply. The allowed bands are narrow.

(b) If the potential barrier strength, and therefore P, is small, the allowed bands become wider (see Fig. 4.12).

(c) If the potential barrier strength becomes smaller and smaller and finally disappears completely, P goes toward zero, and one obtains from (4.67)

or a = k. From this it follows, with (4.46), that

This is the well-known equation (4.8) for free electrons which we derived in Section 4.1.

(d) If the potential barrier strength is very large, P approaches infinity. However, because the left-hand side of (4.67) has to stay within the limits ±1, i.e., it has to remain finite, it follows that

i.e., sin aa ! 0. This is only possible if aa = np or

Figure 4.12. Function P(sin aa/aa) + cos aa with P = p/10.

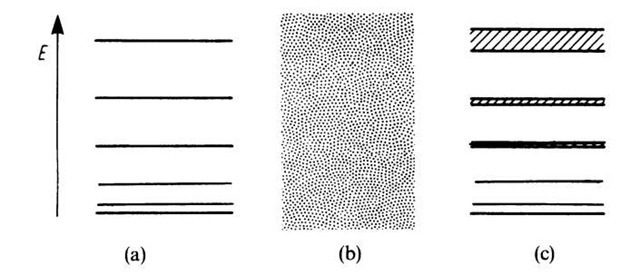
Figure 4.13. Allowed energy levels for (a) bound electrons, (b) free electrons, and (c) electrons in a solid.

Combining (4.46) with (4.69) yields

which is the result of Section 4.2, equation (4.18).

We summarize (Fig. 4.13): If the electrons are strongly bound, i.e., if the potential barrier is very large, one obtains sharp energy levels (electron in the potential field of one ion). If the electron is not bound, one obtains a continuous energy region (free electrons). If the electron moves in a periodic potential field, one receives energy bands (solid).

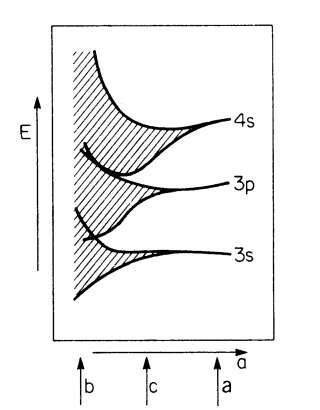
The widening of the energy levels into energy bands and the transition into a quasi-continuous energy region is shown in Fig. 4.14. This widening occurs because the atoms increasingly interact as their separation distance decreases. The arrows a, b, and c refer to the three sketches of Fig. 4.13.

Figure 4.14. Widening of the sharp energy levels into bands and finally into a quasi-continuous energy region with decreasing interatomic distance, a, for a metal (after calculations of Slater). The quantum numbers are explained in topic 3.