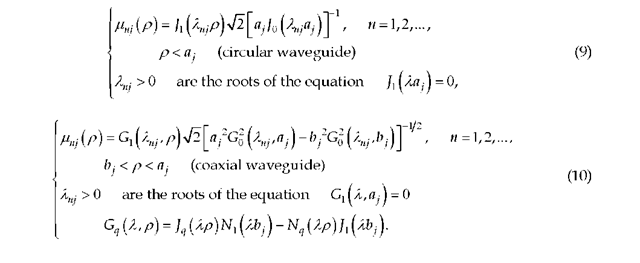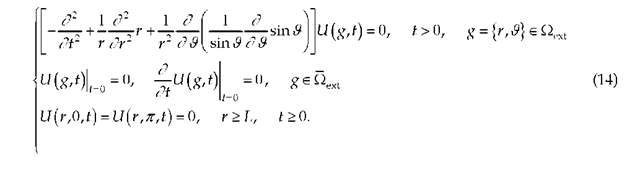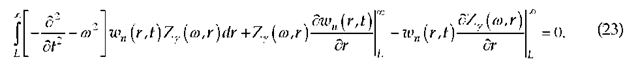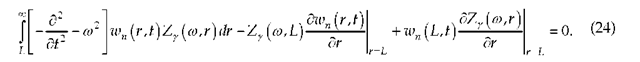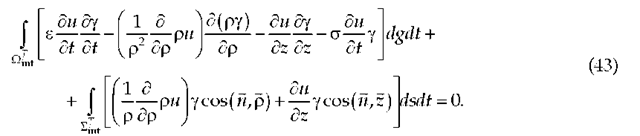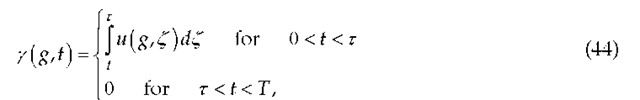Introduction
Present day methodologies for mathematical simulation and computational experiment are generally implemented in electromagnetics through the solution of boundary-value (frequency domain) problems and initial boundary-value (time domain) problems for Maxwell’s equations. Most of the results of this theory concerning open resonators have been obtained by the frequency-domain methods. At the same time, a rich variety of applied problems (analysis of complex electrodynamic structures for the devices of vacuum and solid-state electronics, model synthesis of open dispersive structures for resonant quasi-optics, antenna engineering, and high-power electronics, etc.) can be efficiently solved with the help of more universal time-domain algorithms.
The fact that frequency domain approaches are somewhat limited in such problems is the motivation for this study. Moreover, presently known remedies to the various theoretical difficulties in the theory of non-stationary electromagnetic fields are not always satisfactory for practitioners. Such remedies affect the quality of some model problems and limit the capability of time-domain methods for studying transient and stationary processes. One such difficulty is the appropriate and efficient truncation of the computational domain in so-called open problems, i.e. problems where the computational domain is infinite along one or more spatial coordinates. Also, a number of questions occur when solving far-field problems, and problems involving extended sources or sources located in the far-zone.
In the present work, we address these difficulties for the case of TE0n – and TM0n -waves in axially-symmetrical open compact resonators with waveguide feed lines. Sections 2 and 3 are devoted to problem definition. In Sections 4 and 5, we derive exact absorbing conditions for outgoing pulsed waves that enable the replacement of an open problem with an equivalent closed one. In Section 6, we obtain the analytical representation for operators that link the near- and far-field impulsive fields for compact axially-symmetrical structures and consider solutions that allow the use of extended or distant sources. In Section 7, we place some accessory results required for numerical implementation of the approach under consideration. All analytical results are presented in a form that is suitable for using in the finite-difference method on a finite-sized grid and thus is amenable for software implementation. We develop here the approach initiated in the works by Maikov et al. (1986) and Sirenko et al. (2007) and based on the construction of the exact conditions allowing one to reduce an open problem to an equivalent closed one with a bounded domain of analysis. The derived closed problem can then be solved numerically using the standard finite-difference method (Taflove & Hagness, 2000).
In contrast to other well-known approximate methods involving truncation of the computational domain (using, for example, Absorbing Boundary Conditions or Perfectly Matched Layers), our constructed solution is exact, and may be computationally implemented in a way that avoids the problem of unpredictable behavior of computational errors for large observation times. The impact of this approach is most significant in cases of resonant wave scattering, where it results in reliable numerical data.
Formulation of the initial boundary-value problem
In Fig. 1, the cross-section of a model for an open axially-symmetrical 
resonant are spherical coordinates. By structure is shown, where 
are cylindrical and 
are spherical coordinates. By
we denote perfectly conducting surfaces obtained by rotating the curve 
about the z -axis; 
is a similarly defined surface across which the relative permittivity s( g) and specific conductivity 
change step-wise; these quantities are piecewise constant inside Qint and take free space values outside. Here, 
is the impedance of free space; e0, and |0 are the electric and magnetic constants of vacuum.
Fig. 1. Geometry of the problem in the half-plane 
The two-dimensional initial boundary-value problem describing the pulsed axially- symmetrical TE0n – (Ep = Ez = H^ = 0 ) and T M0n – (Hp = Hz = E^ = 0 ) wave distribution in open structures of this kind is given by
The SI system of units is used. The variable t which being the product of the real time by the velocity of light in free space has the dimension of length. The operators D1, D2 will be described in Section 2 and provide an ideal model for fields emitted and absorbed by the waveguides.
Exact absorbing conditions for virtual boundaries in input-output waveguides
Equations 
in (1) give the exact absorbing conditions for the outgoing pulsed waves Us(1)(g, t) = U (g, t)- Ui(1)(g, t) and Us(2 >(g, t ) = U (g, t) traveling into the virtual waveguides Q1 and Q2, respectively (Sirenko et al., 2007). Ui(1)(g,t) is the pulsed wave that excites the axially-symmetrical structure from the circular or coaxial circular waveguide Q1. It is assumed that by the time t = 0 this wave has not yet reached the boundary T1 . By using conditions (2), we simplify substantially the model simulating an actual electrodynamic structure: the Qj -domains are excluded from consideration while the operators Dj describe wave transformation on the boundaries rj that separate regular feeding waveguides from the radiating unit. The operators Dj are constructed such that a wave incident on rj from the region Qint passes into the virtual domain Qj as if into a regular waveguide – without deformations or reflections. In other words, it is absorbed completely by the boundary rj. Therefore, we call the boundary conditions (2) as well as the other conditions of this kind ‘exact absorbing conditions’.
In the topic (Sirenko et al., 2007), one can find six possible versions of the operators Dj for virtual boundaries in the cross-sections of circular or coaxial-circular waveguides. We pick out two of them (one for the nonlocal conditions and one for the local conditions) and, taking into consideration the location of the boundaries Tj in our problem (in the plane z = -L1 for the boundary T1 and in the plane z = L2 for T2) as well as the traveling direction for the waves outgoing through these boundaries (towards z = -<x> for T1 and towards z = <x> for T2 ), write (2) in the form:
(nonlocal absorbing conditions) and
(local absorbing conditions). The initial boundary-value problems involved in (5) and (6) with respect to the auxiliary functions Wj (p, t, 9) must be supplemented with the following boundary conditions for all times t > 0 :
(on the boundaries p = 0 and p = aj of the region Qj for a circular waveguide) and
Analytical representations for nj (p) and Xnj are well-known and for TE0n -waves take the form:
For TM0n -waves we have:
Here Nq (x) are the Neumann functions. The basis functions 
satisfy boundary conditions at the ends of the appropriate intervals (p < aj or bj < p< aj) and the following equalities hold
in the circular or coaxial waveguide, respectively.
Exact radiation conditions for outgoing spherical waves and exact absorbing conditions for the artificial boundary in free space
When constructing the exact absorbing condition for the wave U (g, t) crossing the artificial spherical boundary T, we will follow the sequence of transformations widely used in the theory of hyperbolic equations (e.g., Borisov, 1996) – incomplete separation of variables in initial boundary-value problems for telegraph or wave equations, integral transformations in the problems for one-dimensional Klein-Gordon equations, solution of the auxiliary boundary-value problems for ordinary differential equations, and inverse integral transforms.
In the domain Qext = Q \ (Qint U T), where the field U(g, t) propagates freely up to infinity as t , the 2-D initial boundary-value problem (1) in spherical coordinates takes the form
Let us represent the solution U(r,S,t) as U(r,S, t) = u(r,t)|(S). Separation of variables in (14) results in a homogeneous Sturm-Liouville problem with respect to the function | (cos S) = |(S)
and the following initial boundary-value problem for u (r, t):
Let us solve the Sturm-Liouville problem (15) with respect to | (cos S) and X . Change of variables x = cosS, |(x) = |(cosS) yields the following boundary-value problem for |(x) :
With X2 = Xn = n(n +1) for each n = 1,2,3,… equation (17) has two nontrivial linearly independent solutions in the form of the associated Legendre functions P^ (x) and Q^ (x). Taking into account the behavior of these functions in the vicinity of their singular points x = +1 (Bateman & Erdelyi, 1953), we obtain
Here 
is a complete orthonormal (with weight function sin S) system of functions in the space L20 <9</)J and provides nontrivial solutions to (15). Therefore, the solution of initial boundary-value problem (14) can be represented as
where the space-time amplitudes un (r,t) are the solutions to problems (16) for X2 = Xn . Our goal now is to derive the exact radiation conditions for space-time amplitudes un (r, t) of the outgoing wave (19). By defining wn (r, t)= run (r, t) and taking into account that Xn = n (n +1), we rewrite equation (16) as
Now subject it to the integral transform
satisfies the equation (Korn & where the kernel
satisfies the equation (Korn & Korn, 1961)
Here a(ro), P(ro) are arbitrary functions independent of r , and a is a fixed real constant. Applying to (20) the transform (21) with a = 1/2 and y = n +1/2, we arrive at
Since the ‘signal’ wn (r, t) propagates with a finite velocity, for any t we can always point a distance r such that the signal has not yet reached it, that is, for these t and r we have wn (r, t) = 0 . Then we can rewrite equation (23) in the form
From (24) the simple differential equation for the transforms 
of the functions 
follows:
In this equation, the values a(ro) and P(ra) entering into Zy(ro, r) are not defined yet. With a(co) = 1 and P(ro) = 0, we have
The last integral is the Hankel transform (Korn & Korn, 1961), which is inverse to itself, and
By % we denote the Heaviside step-function
Taking into account (26), equation (25) can be rewritten in the form
where
and the symbol ”’ denotes derivatives with respect to the whole argument roL .
If G is a fundamental solution of the operator B[G] (i.e., B[G(t)] = S(t), where 8(f) is the Dirac delta function), then the solution to the equation B [U (t)] = g (t) can be written as a convolution U = (G * g) (Vladimirov, 1971). For
we have
and then
Applying the inverse transform (28) to equation (32), we can write
Let us denote
Then from (Gradshteyn & Ryzhik, 2000) we have for r > L > 0
where Py(x) and Qy(x) are the Legendre functions of the first and second kind, respectively. For y = n +1/2, we can rewrite this formula as
denotes a Legendre polynomial. Considering where
denotes a Legendre polynomial. Considering that
(Janke et al., 1960), and d%(x)/dx = S(x), we can derive
Finally, taking into account the relation wn (r, t) = run (r, t), we have from (33)
By using (19), we arrive at the desired radiation condition:
By passing to the limit r ^ L in (40), we obtain
Formula (41) represents the exact absorbing condition on the artificial boundary T . This condition is spoken of as exact because any outgoing wave described by the initial problem (1) satisfies this condition. Every outgoing wave U (g, t) passes through the boundary T without distortions, as if it is absorbed by the domain Qext or its boundary T . That is why this condition is said to be absorbing.
On the equivalence of the initial problem and the problem with a bounded domain of analysis
We have constructed the following closed initial boundary-value problem
where the operator D is given by (41). It is equivalent to the open initial problem (1). This statement can be proved by following the technique developed in (Ladyzhenskaya, 1985).
The initial and the modified problems are equivalent if and only if any solution of the initial problem is a solution to problem (42) and at the same time, any solution of the modified problem is the solution to problem (1). (In the Qext -domain, the solution to the modified problem is constructed with the help of (40).) The solution of the initial problem is unique and it is evidently the solution to the modified problem according construction. In this case, if the solution of (42) is unique, it will be a solution to (1). Assume that problem (42) has two different solutions U1 (g, t) and U2 (g, t). Then the function u (g, t) = U1 (g, t)- U2 (g, t) is also the generalized solution to (42) for
This means that for any function 
that is zero at t = T, the following equality holds:
Here, Q^ = Qint x(0,T) and Sjnt are the space-time cylinder over the domain Qint and its lateral surface; cos (n, p) and cos (n, z) are the cosines of the angles between the outer normal n to the surface STnt and p – and z -axes, respectively; the element dg of the end surface of the cylinder QTnt equals pdpdz . By making the following suitable choice of function,
it is possible to show that every term in (43) is nonnegative (Mikhailov, 1976) and therefore u (g, t) is equal to zero for all g e Qint and 0 < t < T, which means that the solution to the problem (42) is unique. This proves the equivalency of the two problems.
